2023美赛C题:预测Wordle结果-思路详解及参考代码
一、题目解析
总体来看与去年的C题比较相似,唯一一道有数据(不需要自己额外找)的题目,选题人估计也最多。
本质是数据分析题目,需要建立预测模型、分类模型、特征挖掘等。相对来说出思路比较简单,想出彩比较难。所以在分析建模时一定要多维度思考,不然连页数都凑不够。
题目要求:
《纽约时报》已经要求你对此文件中的结果进行分析,以回答几个问题。
•1.报告的结果的数量每天都在变化。开发一个模型来解释这种变化,并使用您的模型为2023年3月1日报告的结果数量创建一个预测区间。单词的任何属性是否会影响在困难模式下玩家的分数的百分比?如果是,如何处理?如果不是,为什么不呢?
这一问要求对数据表中的数据进行分析和解释说明,总结变化规律,并选择合适的预测模型对未来数据进行预测。这里题目指出预测结果应该是一个区间,这说明传统的回归拟合预测不能满足题目要求,需要进行改进或者直接使用基于统计学的区间预测方法。
同时我们还需要分析单词的属性,给出的单词量虽然并不大,但直接对单词进行属性分析需要较深的NLP知识,不好切入。不妨我们可以从结果入手,求出每个单词选择困难模式的玩家平均解题次数作为特征变量进行聚类分析,得到少、适中、多三个或更多的类别,然后可以生成词云图观察对应类别中的词分布特点。分布特点可以人为构造,如统计各个字母出现频次,aeiou元音字母占比(aeiou存在少的往往生僻),重复字母个数(按照题目困难模式下拥有重复的字母会好猜)。分析聚类是否在以上特点中存在显著的分布趋势,即可得到结论。
如果有影响,就在出题中减少这类单词。无影响,说明情况即可。
•2.对于未来日期的给定未来解决方案词,开发一个模型,允许您预测报告结果的分布。换句话说,来预测未来一个日期的(1、2、3、4、5、6、X)的相关百分比。你的模型和预测有哪些不确定性?举一个你在2023年3月1日预测eerie这个词的具体例子。你对你的模型的预测有多有信心?
结合问题一的结论开发预测模型,直接将已知数据其输入预测模型进行训练,调整优化参数后得到预测模型,将新词已知条件输入,输出(1、2、3、4、5、6、X)的值,最后将结果进行归一化处理。(按照3问,该题不需要考虑难易程度)
测量模型的不确定性可以采用蒙特卡罗Dropout法(MC Dropout)和深度集成法。
•3.开发和总结一个模型,按难度分类解决方案词。识别与每个分类关联的给定单词的属性。使用你的模型,怪诞这个词有多难?讨论你的分类模型的准确性。
结合问题一的结论开发预测模型,根据eerie词的特点去给该题的难易程度打分,显而易见,该词并不是一个常见的词汇,难度系数较高。生僻词可以作为一个评价维度,然后用问题一的分布特点作为其他评价指标,用综合评价法求出得分作为词的标签。其他已知词的难以标签则由聚类结果(对应平均分)决定。接着将其输入预测模型进行训练,输出(1、2、3、4、5、6、X)的值,最后将结果进行归一化处理。
测量模型的不确定性可以采用蒙特卡罗Dropout法(MC Dropout)和深度集成法,预测信心可以用训练集的准确率、AUC值来验证,也可以添加噪声来验证模型鲁棒性。
•4.列出并描述了这个数据集的其他一些有趣的特性。最后,在一封给《纽约时报》拼图编辑的一到两页的信中总结你的结果。
数据分析+可视化+总结结果
二、具体步骤及代码
问题一:
首先进行数据分析与可视化,观察规律
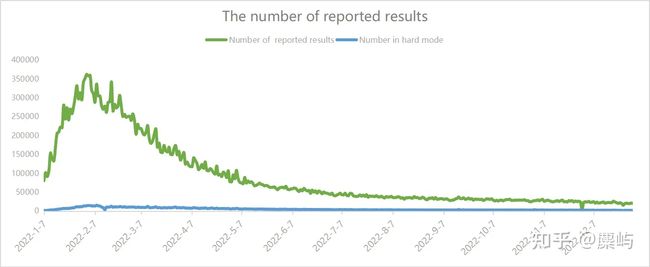
我们发现在记录的日期最开始的时候,报告的数量上升迅速,在2月分左右到达峰值,在较小幅度的震荡波动之后缓慢下降,逐渐稳定下来,维持在一个稳定的数据区间内波动。这说明在游戏推出时,人们由于新鲜感和宣传、传播等大量的涌入游戏网页进行猜谜,然而随着时间的推动,人们失去了新鲜感,逐渐退出,游戏的热度也随之下降。只有一些忠实的玩家会持续进行游戏。
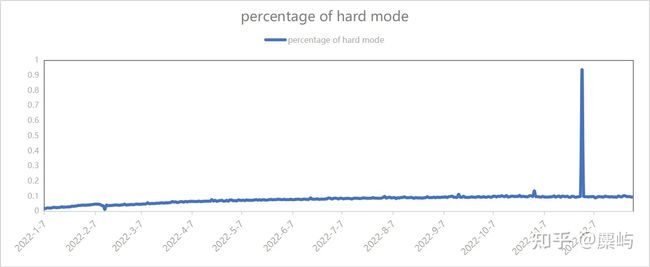
然而,困难模式的相对数量变化波动并不大,我们可以认为,热衷于挑战困难模式的玩家属于一类比较固定的玩家群体。
建立解释变化的模型可以采用简单的拟合多项式模型来解释,也可以利用时间序列的模型来拟合,如移动平均、指数平滑等。
由于前述分析可以看出,数据的变化和时间有着紧密的关系,所以我们可以依赖时间建立预测模型。
由于我们序列的性质比较单一,(无明显季节等特征),可以直接采用holt线性预测方法。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df=pd.read_excel('Problem_C_Data_Wordle.xlsx',skiprows=1)
data=df[['Date','Number of reported results']]
def secondaryExponentialSmoothingMethod(list, n_average, alpha,
day): # 参数list为你要传入的时间序列,n_average表示数列两端取多少个数(要取奇数),alpha为平滑系数,day为向后预测的天数
# 准备好解二元一次方程组的方法
def fangChengZu(a1, b1, a2, b2, c1, c2):
a = np.array([[a1, b1], [a2, b2]])
b = np.array([c1, c2])
x, y = np.linalg.solve(a, b)
return x, y
# 取数列两端各n_average个值加以平均
list_left = list[0:n_average] # data中前n_average个值构成的list
list_right = list[n_average + 1:len(list)] # data中后n_average个值构成的list
list_left_average = np.mean(list_left) # list_left包含元素的均值
list_right_average = np.mean(list_right)
x1 = (n_average + 1) / 2
x2 = (len(list) - x1) + 1
# print(list_left_average,list_right_average)
# 代入线性趋势方程,解出a1,b1
a1, b1 = fangChengZu(1, x1, 1, x2, list_left_average, list_right_average)
# print(a1,b1)
# 代入公式(12),解出S11,S12
S11, S12 = fangChengZu(2, -1, a1, b1, -b1, (alpha / (1 - alpha)))
# print(S11,S12)
a_tao = 0 # 初始化
b_tao = 0
for i in range(len(list)):
S1 = alpha * list[i] + (1 - alpha) * S11
S2 = alpha * S1 + (1 - alpha) * S12
S11 = S1
S12 = S2
a_tao = 2 * S1 - S2
b_tao = (alpha / (1 - alpha)) / (S1 - S2)
H = a_tao + b_tao * day # 预测值
return H
if __name__ == '__main__':
data =data['Number of reported results'] # 时间序列
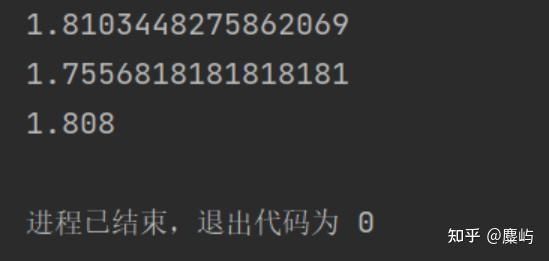
prediction_day1 = secondaryExponentialSmoothingMethod(data, 3, 0.5, 1) #预测下一天
prediction_day2 = secondaryExponentialSmoothingMethod(data, 3, 0.5, 53)#预测3.2号
print(prediction_day2)
plt.figure(figsize=(25, 7))
plt.plot(data,color='b', label='Original')
plt.plot(414,prediction_day2,color='c', label='Predict',marker='+')
plt.show()或者采用简单参数的arima算法。
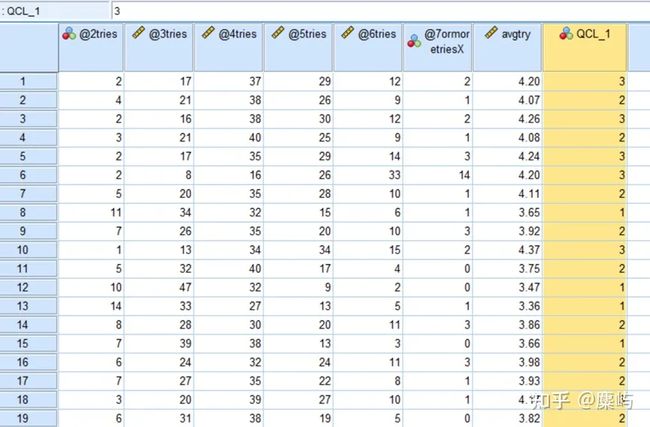
接下来为了判断词的特性,我们先先求出平均解题次数(因为X的不确定性,我们忽略该项),直接用SPSS进行k-means聚类分析。
分类结果
不同类对应词特征