pytorch学习笔记九：权值初始化

一、概念

权值初始化是指在网络模型训练之前，对各节点的权值和偏置初始化的过程，正确的初始化会加快模型的收敛，从而加快模型的训练速度，而不恰当的初始化可能会导致梯度消失或梯度爆炸，最终导致模型无法训练。

如上图所示的一个基本的CNN网络结构，数据在网络结构中流动时，会有如下的公式（默认没有偏置）：

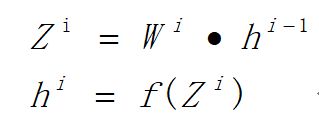
在反向传播的过程中，由于是复合函数的求导，根据链式求导法则，会有两组导数，一个是损失函数Cost对Z的导数，一个是损失函数对W的导数，
1、损失函数关于状态Z的梯度：

2、损失函数关于W的梯度：

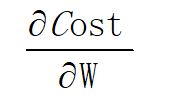
可以看出，在网络结构中，一个参数的初始化关系到网络能否训练出好的结果或者以多快的速度收敛。所以对权值初始化有如下的要求：

• 参数不能全部初始化为0或全为1，也不能全部初始化同一个值；（反向传播时梯度的更新值一样）
• 参数的初始化值不能太大；（针对激活函数是sigmoid和tanh，参数太大，梯度会消失）
• 参数的初始化值也不能太小；（针对激活函数是relu和sigmoid，参数太小，梯度会消失）

所有的参数初始化为0或者相同的数
最简单的初始化方法是将所有的参数初始化为0或者一个常数，但是使用这种特征会使网络中的所有神经元学习到的是相同的特征。
假设神经网络中只有一个有2个神经元的隐藏层，现在将偏置参数初始化为：bias=0，权值矩阵初始化为一个常数α。 网络的输入为(x1,x2)，隐藏层使用的激活函数为ReLU，则隐藏层的每个神经元的输出都是relu(αx1+αx2)。 这就导致，对于loss function的值来说，两个神经元的影响是一样的，在反向传播的过程中对应参数的梯度值也是一样，也就说在训练的过程中，两个神经元的参数一直保持一致，其学习到的特征也就一样，相当于整个网络只有一个神经元。

过大或过小的初始化
如果权值的初始值过大，则会导致梯度爆炸，使得网络不收敛；过小的权值初始值，则会导致梯度消失，会导致网络收敛缓慢或者收敛到局部极小值。如果权值的初始值过大，则loss function相对于权值参数的梯度值很大，每次利用梯度下降更新参数时，参数更新的幅度也会很大，这就导致loss function的值在其最小值附近震荡。而过小的初始值则相反，loss关于权值参数的梯度很小，每次更新参数时，更新的幅度也很小，着就会导致loss的收敛很缓慢，或者在收敛到最小值前在某个局部的极小值收敛了。

所以不恰当的初始化可能会引起梯度消失或梯度爆炸，所以下面来了解一下什么是梯度消失与爆炸

二、梯度消失与爆炸

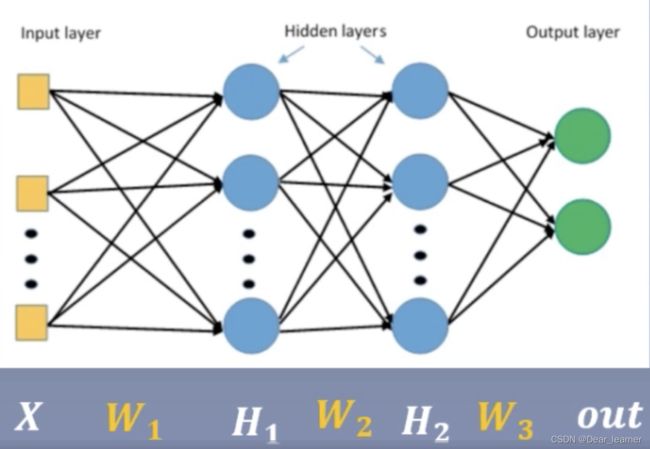
以上图所示的三层全连接网络为例，假设要计算W2的梯度，根据链式求导法则如下：H2 = H1 * W1

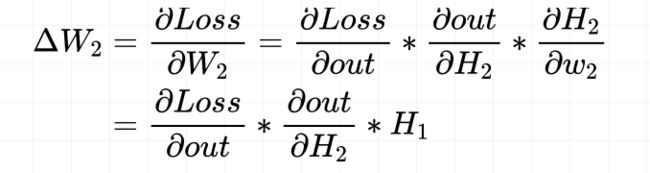
W2的梯度回用到上一层神经元的输出H1，如果H1的输出非常小，那么W2的梯度也会非常小，这就可能会造成梯度消失的现象，尤其是当网络层数增多时，乘以一个小值后面权值的梯度会更小，甚至会消失。这就使得损失函数得不到更新，模型的训练会停滞。而当H1的输出非常大时，W2的梯度会非常大，就会发生梯度爆炸。

一旦发生梯度消失或者爆炸，就会导致模型无法训练，而如果想避免这个现象，就得控制网络输出层的一个尺度范围，也就是不能让它太大或者太小。这就需要对权值进行合理的初始化，下面从代码中来理解一下：

建立一个layer=100的多层感知机，其中每层的神经元个数neural_num=256，如下：

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)

            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break

        return x

    def initialize(self):
        """
        权值初始化部分
        """
        for m in self.modules():
            if isinstance(m, nn.Linear):
                # 使用标准正态对权值进行初始化，mean=0, std=1
                nn.init.normal_(m.weight.data)
 layer_nums = 100
 neural_nums = 256
 batch_size = 16

 net = MLP(neural_nums, layer_nums)
 net.initialize()

 inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1

 output = net(inputs)
 print(output)             

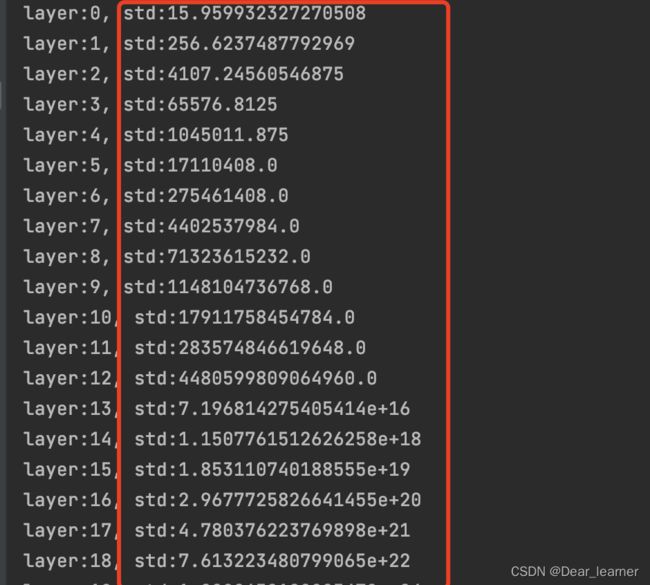
输出结果如下：

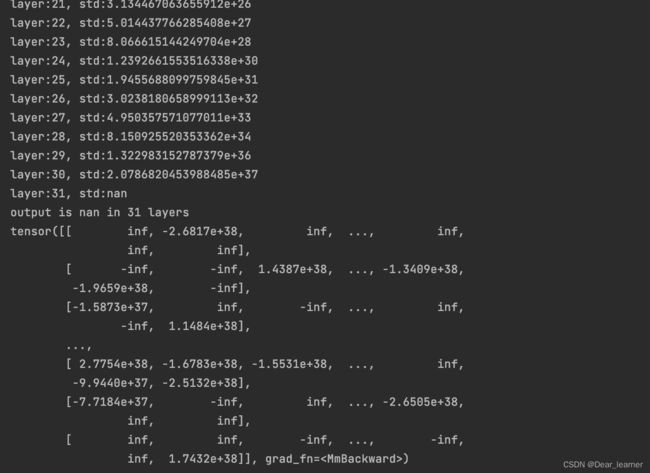
从输出结果可看出，随着层数的增加，网络输出的标准差也在增大，在第31层时，由于数据超出了当前精度所表示的范围，输出值变为nan，这说明网络出现了问题，导致输出的结果太大，而在反向传播时，根据上面的公式，权重的梯度无法得到更新，会出现梯度爆炸的现象。所以就会出现网络输出的结果为nan的现象，如下：

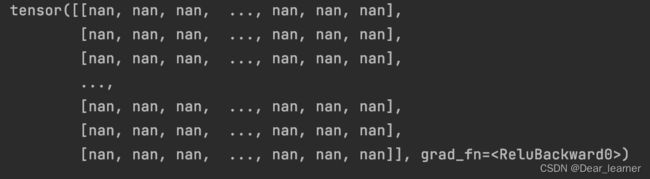
Q：在上面的输出结果中，为什么随着层数的增加，网络输出的标准差会越来越大
A：从方差的推导公式说起
概率论中三个基本公式

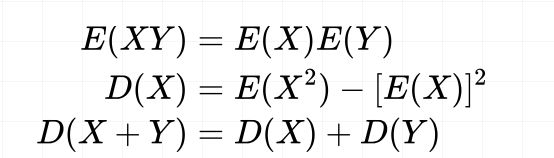
那么

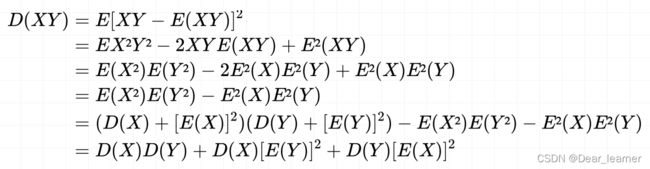
若E(X)=0, E(Y)=0，则 D(XY) = D(X)D(Y)
神经网络里每一层输出的方差计算：

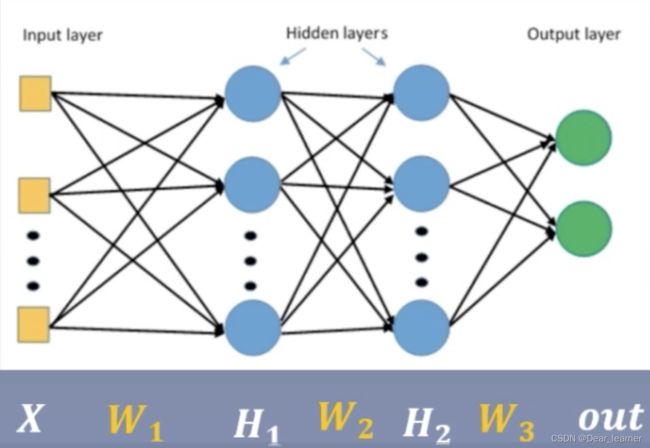
来计算一下第一层第一个神经元的方差：

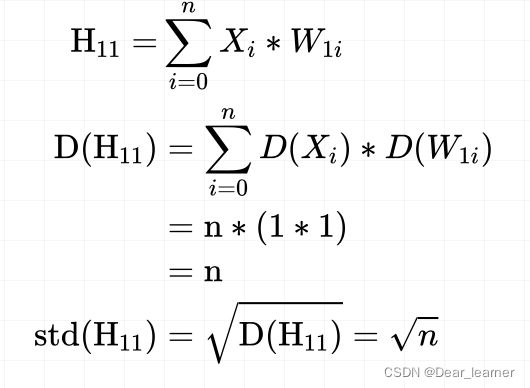
输入的数据和权值都是均值为0，方差为1的标准正态分布，而经过一个网络层方差就会扩大n倍，所以输出值标准差会随着网络层数的增加呈现指数的增长，当超出精度时，就会出现nan。从上面的示例的输出结果就能验证这一点

那么要如何解决这一问题呢？答案是，让网络层输出的方差尺度保持不变就可以了。具体要如何实现呢，从网络层的输出方差来分析：

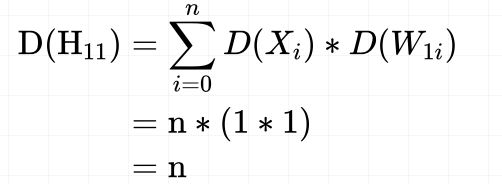
从上面公式可看出，每一层输出的方差由三个因素决定，网络层神经元的个数n，输入值x的方差和网络层权值w的方差。如果想要方差的尺度保持不变，这里因为是多个数的连乘，让每一层的输出方差都是1，即D(H11) = 1,这样后面多层相乘时，方差的尺度也不会改变。由于神经元的个数n和输入值x的方差不会变，这里就要更改权值w的方差，使得网络层输出的方差为1，

所以在权值初始化时让标准差为 $\sqrt{\frac{1}{n}}$，这样在每一层输出的方差都为1，就不会出现nan的情况了
对上面的代码做如下修改：

def initialize(self):
    for m in self.modules():
        if isinstance(m, nn.Linear):
            nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))    # normal: mean=0, std=1

输出结果如下：

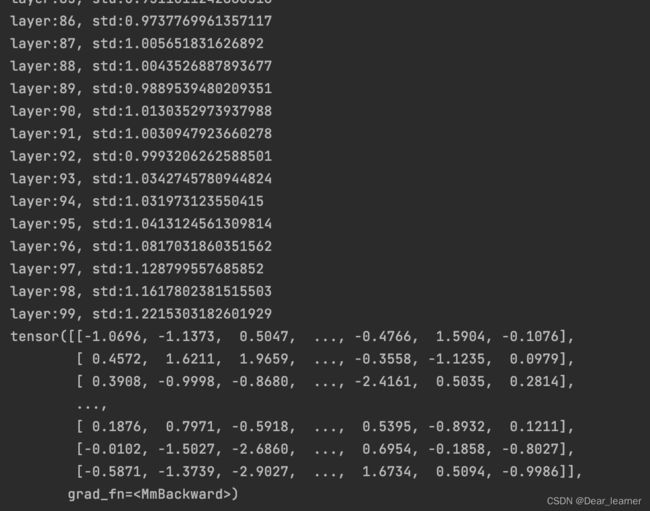
所以只要采用恰当的权值初始化方法，就可以实现多层网络的输出尺度保持在一定的范围内，这样在反向传播的时候，有利用缓解梯度消失或者梯度爆炸的情况。

上面的网络只是一个线性网络，没有添加激活函数，如果在网络的前向传播中增加一个激活函数，来看一下输出结果：

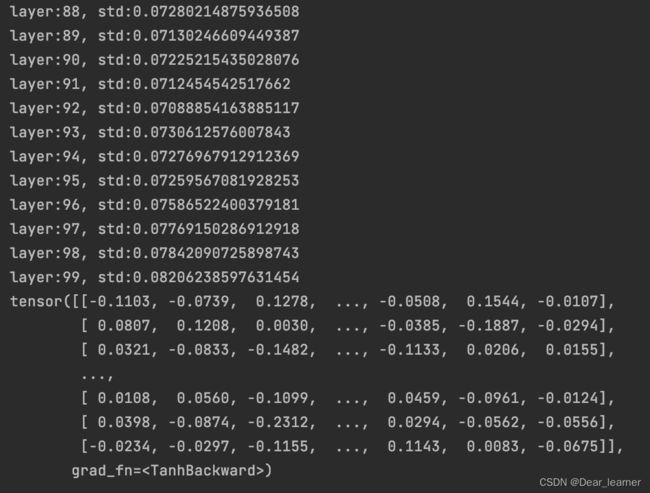
在线性层后添加激活函数torch.tanh()，可以看出网络的输出变得越来越小了，从而会导致梯度的消失，所以下面来了解针对有激活函数的权值初始化方法。

三、权值初始化方法

1、Xavier 初始化

Xavier初始化是在2010年由Glorot等人提出，思想就是尽可能的让输入和输出服从相同的分布，即保持输入和输出的方差一致。

方差一致性：保持数据尺度范围维持在恰当范围，通常方差为 1。
激活函数：饱和函数，如sigmoid、tanh
根据公式推导，权值的方差为：

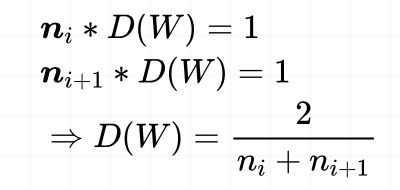
这里的ni和ni+1 分别是指输入层和输出层神经元的个数。
Xavier采用均匀分布对权值初始化
均匀分布的表达式

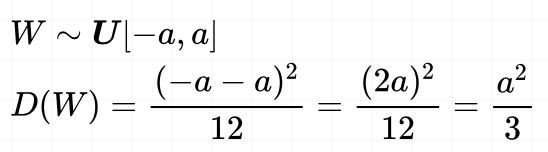
所以权值参数分布服从：

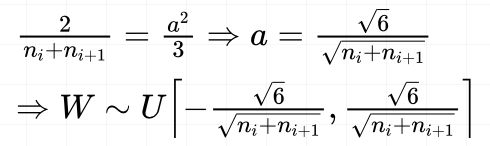
Xavier采用正态分布对权值初始化
基于正太分布的Xavier初始化权值参数服从均值为0，方差为：

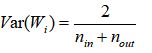
所以权值参数服从正态分布：

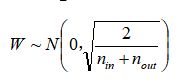
下面用代码实现基于均匀分布的Xavier权值初始化：

def initialize(self):
  for m in self.modules():
    if isinstance(m, nn.Linear):
      # Xavier初始化权重
      tanh_gain = nn.init.calculate_gain('tanh')
      nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)

这里用到nn.init.calculate_gain(nonlinearity, param=None)函数，这个函数的主要作用是计算激活函数的方差变化尺度。就是输入数据的方差除以经过激活函数之后的输出数据的方差。nonlinearity 表示激活函数的名称，如tanh。param 表示激活函数的参数，如 Leaky ReLU 的negative_slop。
输出结果为：

所以Xavier权重初始化，有利于缓解带有sigmoid，tanh的这样的饱和激活函数的神经网络的梯度消失和爆炸现象。

2、Kaiming 初始化

Kaiming 初始化是由何凯明等人提出，只考虑输入的个数，是一个0均值，方差为$\sqrt{\frac{1}{n}}$ 的高斯分布，权值方差的推导过程如下：
对于第L层，有如下的推导：

其中Xl是当前层的输入，也是上一层激活后的输出值，yl是当前输入到激活函数的值，Wl和bl是权值和偏置，其中Xl和Wl但是独立同分布的，则有：

设wl的均值为0，即E(wl)=0,则有：

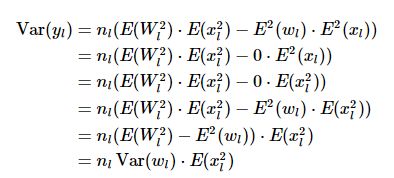
这里和Xavier有一个很大的不同是没有假设输入的值均值为0。这是由于使用激活函数RELU,xl=max(0,yl-1),每层的输出值不可能均值为0.上面最终得到:

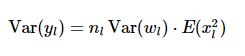
初始化时通常设，w的均值为0，偏置b=0，以及w和x是相互独立的，则有

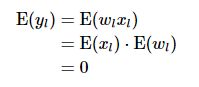
也就是说yl的均值为0.
假设W是关于0对称分布的，则可以得到yl在0附近也是对称分布的，这样使用激活函数，则有

由于只有当yl-1>0的部分，xl才有值，且yl在0附近也是对称分布的，则可以得到

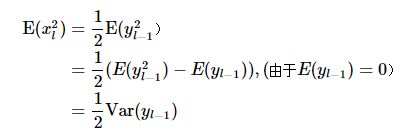
将上面得到的结果带入到

则可以得到

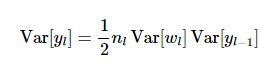
将所有的方差累加到一起有

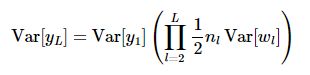
为了使每一层的方差不变，则有

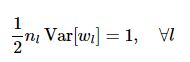
所以权值矩阵的方差为

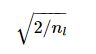
和Xavier一样，使用正态分布或者均匀分布来获得权值矩阵的值。
均匀分布

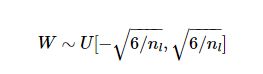
正态分布

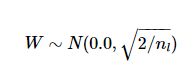
代码实现：

def initialize(self):
  for m in self.modules():
    if isinstance(m, nn.Linear):
      nn.init.kaiming_normal_(m.weight.data)
      # nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num)) 

输出结果:

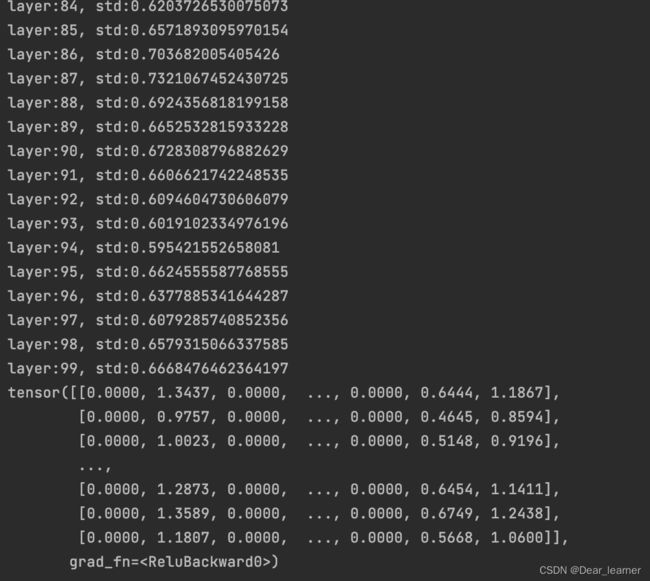
【总结】
权重初始化对于模型的训练至关重要，不好的权重初始化方法会引起输出层的输出值过大过小，从而引发梯度的消失或者爆炸，最终导致模型无法训练。所以如果想缓解这种现象，就得控制输出层的值的范围尺度，就得采取合理的权重初始化方法。