pytorch学习笔记十一：损失函数
一、损失函数是什么
损失函数：衡量模型输出与真实标签之间的差异。与损失函数有关的还有代价函数和目标函数。
- 损失函数（Loss Function）：计算一个样本的差异， L o s s = f ( y ^ , y ) Loss=f\left ( \hat{y},y \right ) Loss=f(y^,y)
- 代价函数（Cost Function）：计算整个训练集loss的一个平均值， c o s t = 1 N ∑ i N f ( y ^ , y ) cos t= \frac{1}{N}\sum_{i}^{N}f\left ( \hat{y},y \right ) cost=N1∑iNf(y^,y)
- 目标函数（Objective Function）：衡量模型的整体拟合程度，过拟合和欠拟合，obj = cost + Regularization
所以在衡量模型的输出和真实标签之间的差异时的损失函数其实是指代价函数，下面看一下pytorch中的损失函数：
_loss也继承了nn.Module类，说明loss也是一层，也有nn.Module中的8个参数字典。参数有size_average、reduce、reduction，其中size_average和reduce已经被舍弃不再使用，重点关注reduction参数。下面以人民币的二分类中交叉熵损失函数为例，看损失函数是如何创建和使用的，背后运行的机制是什么？
# 在train.py文件的损失函数创建处打上断点，进行调试
criterion = nn.CrossEntropyLoss()
可看出程序进入到了loss.py文件中的 CrossEntropyLoss(_WeightedLoss):交叉熵损失类的__init__方法， 这里发现交叉熵损失函数继承_WeightedLoss这个类：
继续debug，就到了class _WeightedLoss(_Loss):这个类里面，就会发现这个类继承_Loss, 那么我们继续步入，就到了_Loss这个类里面去，会发现这个继承Module
在_loss中继承了Module类，所以损失函数的初始化和模型的初始化类似，也调用了Module初始化方法，最终会有8个属性字典，如下：
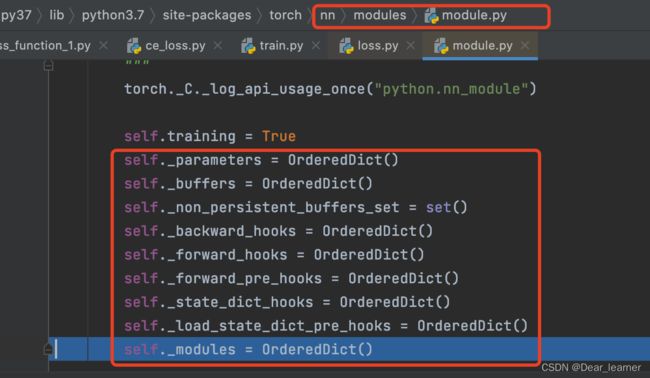
然后在_loss类中设置reduction参数，至此，损失函数的创建过程已完成。下面看一下损失函数的运行机制
# 在此处设置断点，损失函数前向传播
loss = criterion(outputs, labels)
损失函数_loss继承了Module，那么在前向传播时也会调用Module的forward方法，继续debug可看到
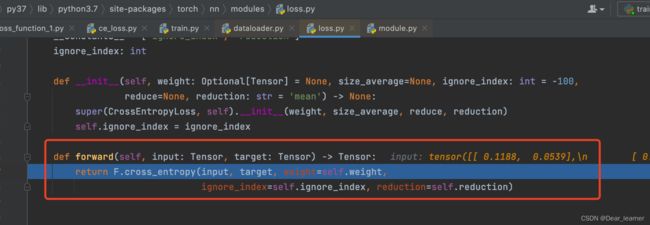
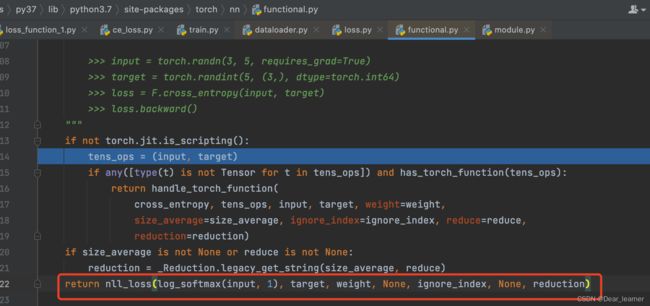所以在forward中调用了F中对应的损失函数，而cross_entroy又是由nll_loss计算而来。以上就是损失函数的创建和内部运行机制。
下面来看pytorch中损失函数的具体使用。
常见损失函数
官网链接
1、交叉熵损失 CrossEntropyLoss
nn.CrossEntropyLoss: nn.LogSortmax() 与 nn.NLLLoss() 结合，进行交叉熵计算。
torch.nn.CrossEntropyLoss(weight=None,
size_average=None,
ignore_index=- 100,
reduce=None,
reduction='mean', label_smoothing=0.0)
参数：
- weight：各类别的loss设置权值
- ignore_index：忽略某个类别
- reduction：计算模式，可为none/sum/mean，none 表示逐个元素计算，这样有多少个样本就会返回多少个 loss。sum 表示所有元素的 loss求和，返回标量，mean 所有元素的 loss 求加权平均（加权平均的含义下面会提到），返回标量。
在了解交叉熵之前先来了解几个概念：
自信息：单个事件的不确定性， I ( x ) = − l o g [ p ( x ) ] I(x) = -log[p(x)] I(x)=−log[p(x)]
熵（信息熵）：描述一个事件的不确定性，一个事件越不确定，熵越大， H ( P ) = E x ∼ p [ I ( x ) ] = − ∑ i N P ( x i ) l o g P ( x i ) H(P)=E_{x\sim p}[I(x)] = -\sum_{i}^{N}P(x_{i})logP(x_{i}) H(P)=Ex∼p[I(x)]=−∑iNP(xi)logP(xi)
交叉熵：衡量两个分布之间的差异程度，P表示数据的原始分布，Q表示模型的输出分布，交叉熵越小说明两个分布越接近 ， H ( P , Q ) = − ∑ i = 1 N P ( x i ) l o g Q ( x i ) H(P, Q) = -\sum_{i=1}^{N}P(x_{i})logQ(x_{i}) H(P,Q)=−∑i=1NP(xi)logQ(xi)，交叉熵 = 信息熵 + 相对熵
相对熵（KL散度）：形容两个分布之间的差异，也就是两个分布之间的距离（注意不是距离函数，不具备对称性） ，
D K L ( P , Q ) = E x ∼ p [ l o g P ( x ) Q ( x ) ] D_{KL}(P,Q)=E_{x\sim p}[log\frac{P(x)}{Q(x)}] DKL(P,Q)=Ex∼p[logQ(x)P(x)],其中P是真实的分布，Q是模型的输出分布
下面对相对熵的公式展示，来看一下相对熵、信息熵和交叉熵之间的关系
所以根据上面的推导可以得到：
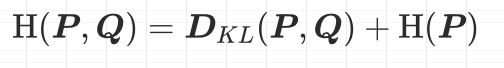
在机器学习模型中，优化交叉熵其实是优化相对熵，这是因为训练集的数据取出来之后它的信息熵H§是固定的。
回到上面交叉熵nn.CrossEntropyLoss: nn.LogSortmax() 与 nn.NLLLoss() 结合，进行交叉熵计算。
从上面的推导可知，交叉熵其实是衡量两个分布之间的距离，所以这里将输出值转化到概率取值的一个范围。这里交叉熵的计算是：
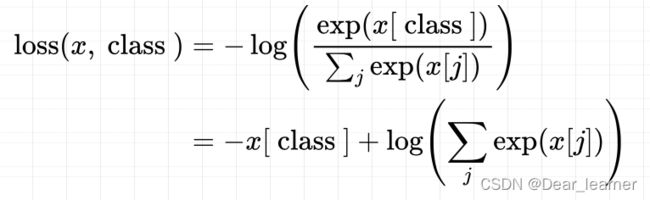
x是输出的概率值，class是某个类别，在括号里面执行的是softmax，把神经元的输出归一化成概率取值，然后取对数的负值得到交叉熵损失函数，对比一下之间的损失函数
由于是某个样本，这里的P(xi)=1，求和符号也没有了。即是loss(x,class)的表达式
再看一下nn.CrossEntropyLoss中的参数weight：各类别的loss设置权重，如果模型中的类别不均衡，设置这个参数很有必要，设置这个参数之后损失函数的表达式为：
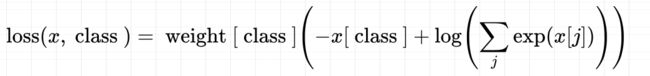
如果想让模型更关注某一类别的话，可以把这一类别的权值设置大一点。
下面从代码中了解一下nn.CrossEntropyLoss
首先设置模型的输出值
# 模型预测的输出，两个类别
inputs = torch.tensor([[1, 2], [1, 3], [1, 3]], dtype=torch.float)
target = torch.tensor([0, 1, 1], dtype=torch.long) # 这里的类型必须是torch.long，两个类别0和1
计算三种模式的损失函数
loss_f_none = nn.CrossEntropyLoss(weight=None, reduction='none')
loss_f_sum = nn.CrossEntropyLoss(weight=None, reduction='sum')
loss_f_mean = nn.CrossEntropyLoss(weight=None, reduction='mean')
# forward
loss_none = loss_f_none(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)
# view
print("Cross Entropy Loss:\n ", loss_none, loss_sum, loss_mean)
输出结果：
根据交叉熵的计算公式来验证一个输出结果
idx = 0
input_1 = inputs.detach().numpy()[idx] # [1, 2]
target_1 = target.numpy()[idx] # [0]
# 第一项
x_class = input_1[target_1]
# 第二项
sigma_exp_x = np.sum(list(map(np.exp, input_1)))
log_sigma_exp_x = np.log(sigma_exp_x)
# 输出loss
loss_1 = -x_class + log_sigma_exp_x
print("第一个样本loss为: ", loss_1)
输出结果：
设置参数weight
# def loss function
weights = torch.tensor([1, 2], dtype=torch.float)
# weights = torch.tensor([0.7, 0.3], dtype=torch.float)
loss_f_none_w = nn.CrossEntropyLoss(weight=weights, reduction='none')
loss_f_sum = nn.CrossEntropyLoss(weight=weights, reduction='sum')
loss_f_mean = nn.CrossEntropyLoss(weight=weights, reduction='mean')
# forward
loss_none_w = loss_f_none_w(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)
# view
print("\nweights: ", weights)
print(loss_none_w, loss_sum, loss_mean)
输出结果：
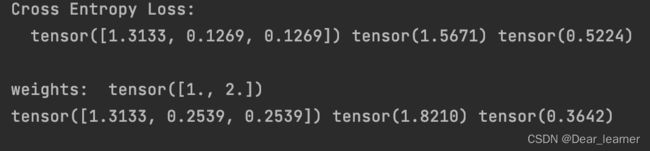
从输出结果可看出，给类别加上权值之后，对应样本的损失函数就会相应的加倍，这里看一下加weight之后的mean是如何计算的：
三个样本，第一个权值是1，后两个的权值是2，所以分母不再是3，而是1+2+2=5，所以mean 模式下求平均不是除以样本的个数，而是样本所占的权值的总份数。
2、nn.NLLoss
功能：实现负对数似然函数中的负号功能
主要参数：
- weight：各类别loss的权值设置
- ignore_index：忽略某个类别
- reduction：计算模式，可为none/mean/sum
none-逐个元素计算
sum-所有元素求和，返回标量
mean-加权平均，返回标量
weights = torch.tensor([1, 1], dtype=torch.float)
loss_f_none_w = nn.NLLLoss(weight=weights, reduction='none')
loss_f_sum = nn.NLLLoss(weight=weights, reduction='sum')
loss_f_mean = nn.NLLLoss(weight=weights, reduction='mean')
# forward
loss_none_w = loss_f_none_w(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)
# view
print("\nweights: ", weights)
print("NLL Loss", loss_none_w, loss_sum, loss_mean)
输出结果：
3、nn.BCELoss
功能：二分类交叉熵
注意事项：输入值取值在[0, 1]
主要参数：
- weight：各类别loss的权值设置
- ignore_index：忽略某个类别
- reduction：计算模式，可为none/mean/sum
none-逐个元素计算
sum-所有元素求和，返回标量
mean-加权平均，返回标量
inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)
target_bce = target
# itarget
# 用sigmoid函数要将输出值转化到0到1之间，否则会报错
inputs = torch.sigmoid(inputs)
weights = torch.tensor([1, 1], dtype=torch.float)
loss_f_none_w = nn.BCELoss(weight=weights, reduction='none')
loss_f_sum = nn.BCELoss(weight=weights, reduction='sum')
loss_f_mean = nn.BCELoss(weight=weights, reduction='mean')
# forward
loss_none_w = loss_f_none_w(inputs, target_bce)
loss_sum = loss_f_sum(inputs, target_bce)
loss_mean = loss_f_mean(inputs, target_bce)
# view
print("\nweights: ", weights)
print("BCE Loss", loss_none_w, loss_sum, loss_mean)
输出结果：
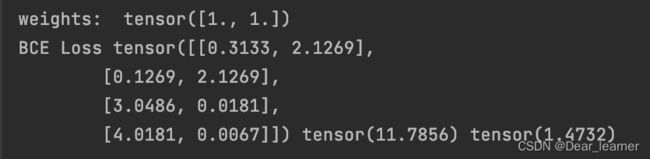
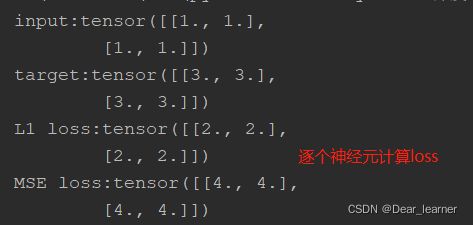
从输出结果可看出，是每个神经元一一对应的去计算loss，而不是一整个神经元去计算loss。
4、nn.BCEWithLogitsLoss
功能：结合sigmoid和二分类交叉熵
注意事项：网络最后的输出不加sigmoid函数
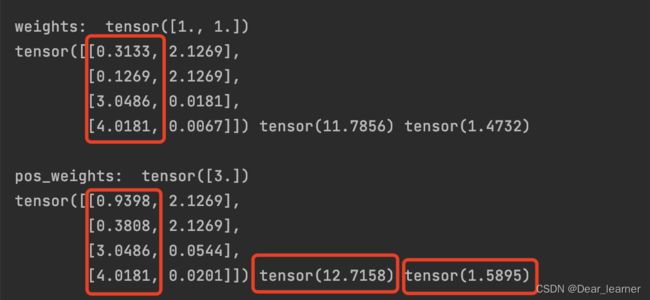
参数：pos_weight:正样本的权值，用来平衡正负样本，比如正样本有100个，负样本有300个，这个参数可设置为3，在类别不平衡时可以使用。
inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)
target_bce = target
# inputs = torch.sigmoid(inputs)
weights = torch.tensor([1, 1], dtype=torch.float)
loss_f_none_w = nn.BCEWithLogitsLoss(weight=weights, reduction='none')
loss_f_sum = nn.BCEWithLogitsLoss(weight=weights, reduction='sum')
loss_f_mean = nn.BCEWithLogitsLoss(weight=weights, reduction='mean')
# forward
loss_none_w = loss_f_none_w(inputs, target_bce)
loss_sum = loss_f_sum(inputs, target_bce)
loss_mean = loss_f_mean(inputs, target_bce)
# view
print("\nweights: ", weights)
print(loss_none_w, loss_sum, loss_mean)
输出结果：
设置pos_weight的输出结果：
5、nn.L1Loss
功能：用于回归问题，计算inputs和target之差的绝对值,返回同维度的tensor或者一个标量
6、nn.MSELoss
功能 ：用于回归问题，计算inputs与target之差的平方
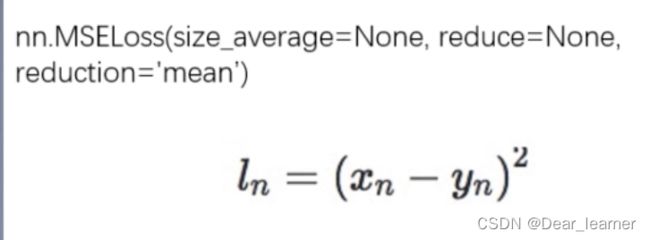
代码实现：
inputs = torch.ones((2, 2))
target = torch.ones((2, 2)) * 3
loss_f = nn.L1Loss(reduction='none')
loss = loss_f(inputs, target)
print("input:{}\ntarget:{}\nL1 loss:{}".format(inputs, target, loss))
loss_f_mse = nn.MSELoss(reduction='none')
loss_mse = loss_f_mse(inputs, target)
print("MSE loss:{}".format(loss_mse))
输出结果：
7、nn.SmoothL1Loss
平滑的L1Loss，计算公式如下：
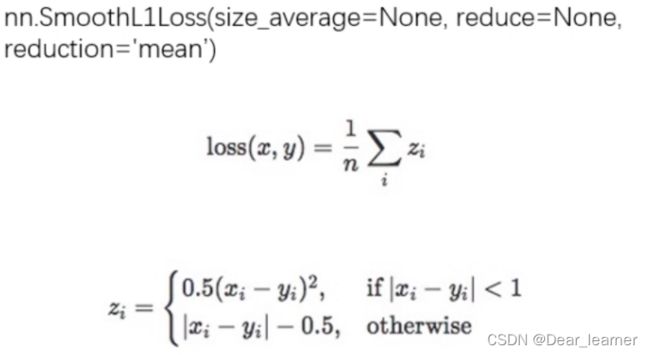
和L1Loss的示意图：
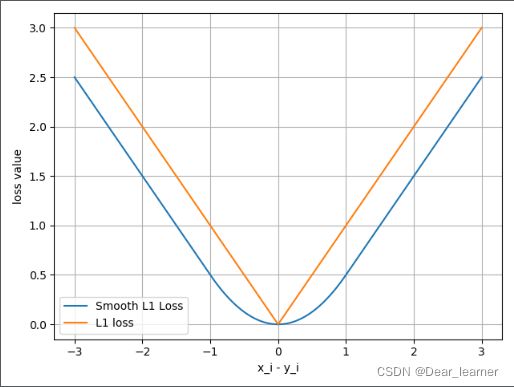
采用这种平滑的损失函数可以减轻离群点带来的影响。
8、nn.PoissonNLLLoss
功能：泊松分布的负对数似然损失函数，分类里面如果发现数据的类别服从泊松分布，可以使用这个损失函数
主要参数：
log_input：输入是否为对数形式，决定计算公式
full：计算所有的loss，默认为False
eps：修正项，避免log(input)为nan
9、nn.KLDivLoss
功能：计算KLD，KL散度，相对熵
注意事项：需要提前将输入计算 log-probabilities，如通过 nn.logsoftmax()
代码实现：
inputs = torch.tensor([[0.5, 0.3, 0.2], [0.2, 0.3, 0.5]])
# pytorch函数计算公式不是原始定义公式，其对输入默认已经取log了，在损失函数计算中比公式定义少了一个log（input）的操作
# 因此公式定义里有一个log(y_i / x_i)，在pytorch变为了 log(y_i) - x_i，
inputs = F.log_softmax(inputs, 1)
target = torch.tensor([[0.9, 0.05, 0.05], [0.1, 0.7, 0.2]], dtype=torch.float)
loss_f_none = nn.KLDivLoss(reduction='none')
loss_f_mean = nn.KLDivLoss(reduction='mean')
loss_f_bs_mean = nn.KLDivLoss(reduction='batchmean')
loss_none = loss_f_none(inputs, target)
loss_mean = loss_f_mean(inputs, target)
loss_bs_mean = loss_f_bs_mean(inputs, target)
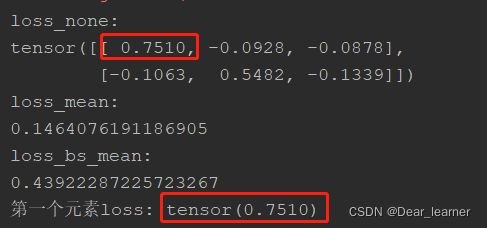
print("loss_none:\n{}\nloss_mean:\n{}\nloss_bs_mean:\n{}".format(loss_none, loss_mean, loss_bs_mean))
### compute by hand
idx = 0
loss_1 = target[idx, idx] * (torch.log(target[idx, idx]) - inputs[idx, idx])
print("第一个元素loss:", loss_1)
输出结果：
10、nn.MarginRankingLoss
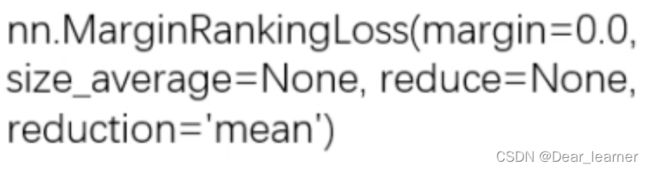
功能：计算两个向量之间的相似度，用于排序任务。特别说明，该方法计算两组数据之间的差异，也就是每个元素两两之间都会计算差异，返回一个 n*n 的 loss 矩阵。类似于相关性矩阵那种。
主要参数：
margin：边界值，x1与x2之间的差异值，计算公式如下：
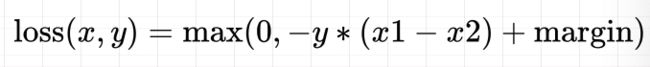
y=1时，希望x1比x2大，当x1>x2时，不产生loss
y=-1时，希望x2比x1大，当x2>x1时，不产生loss
x1 = torch.tensor([[1], [2], [3]], dtype=torch.float)
x2 = torch.tensor([[2], [2], [2]], dtype=torch.float)
target = torch.tensor([1, 1, -1], dtype=torch.float)
loss_f_none = nn.MarginRankingLoss(margin=0, reduction='none')
loss = loss_f_none(x1, x2, target)
print(loss)
输出结果：
11、nn.MultiLabelMarginLoss
功能：多标签边界损失函数，属于多标签分类，一个样本可能属于多个类，
计算公式如下：
这里的 i 取值从 0 到输出的维度减 1，j 取值也是 0 到 y 的维度减 1，对于所有的 i 和 j，i 不等于 y[j]，也就是标签所在的神经元去减掉那些非标签所在的神经元
例如：四分类任务，样本x属于0类和3类，标签是 [0, 3, -1, -1]，而不是[1, 0, 0, 1]
x = torch.tensor([[0.1, 0.2, 0.4, 0.8]])
y = torch.tensor([[0, 3, -1, -1]], dtype=torch.long)
loss_f = nn.MultiLabelMarginLoss(reduction='none')
loss = loss_f(x, y)
print(loss)
### compute by hand
x = x[0]
# 因为属于第0类，用标签所在的神经元减去非标签所在的神经元
item_1 = (1-(x[0] - x[1])) + (1 - (x[0] - x[2])) # [0] 第0类
item_2 = (1-(x[3] - x[1])) + (1 - (x[3] - x[2])) # [3] 第三类
loss_h = (item_1 + item_2) / x.shape[0]
print(loss_h)
输出结果：
12、nn.SoftMarginLoss
功能：计算二分类的logistic损失
计算公式如下：
inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]])
target = torch.tensor([[-1, 1], [1, -1]], dtype=torch.float)
loss_f = nn.SoftMarginLoss(reduction='none')
loss = loss_f(inputs, target)
print("SoftMargin: ", loss)
### compute by hand
idx = 0
inputs_i = inputs[idx, idx]
target_i = target[idx, idx]
loss_h = np.log(1 + np.exp(-target_i * inputs_i))
print(loss_h)
输出结果：
13、nn.MultiLabelSortMarginLoss
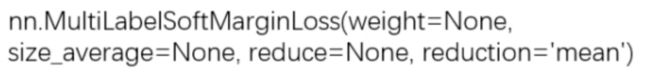
功能：SoftMarginLoss 多标签版本 （多标签问题）
计算公式如下：
C表示标签的数量（类别），i是神经元的个数，标签是[1, 0, 0, 1],
inputs = torch.tensor([[0.3, 0.7, 0.8]])
target = torch.tensor([[0, 1, 1]], dtype=torch.float)
loss_f = nn.MultiLabelSoftMarginLoss(reduction='none')
loss = loss_f(inputs, target)
print("MultiLabel SoftMargin: ", loss)
### compute by hand
i_0 = torch.log(torch.exp(-inputs[0, 0]) / (1 + torch.exp(-inputs[0, 0])))
i_1 = torch.log(1 / (1 + torch.exp(-inputs[0, 1])))
i_2 = torch.log(1 / (1 + torch.exp(-inputs[0, 2])))
loss_h = (i_0 + i_1 + i_2) / -3
print(loss_h)
输出结果：
14、nn.MultiMarginLoss（hingLoss）
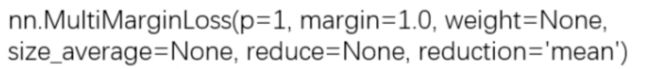
功能：计算多分类的折页损失（多分类问题）
这里的 p 可选 1 或者 2，margin 表示边界值。计算公式如下：
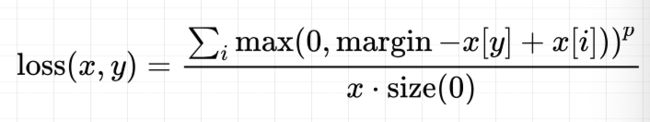
x[y]是标签所在的神经元，x[i]是非标签所在的神经元，i 非标签的神经元的个数。
x = torch.tensor([[0.1, 0.2, 0.7], [0.2, 0.5, 0.3]])
y = torch.tensor([1, 2], dtype=torch.long)
loss_f = nn.MultiMarginLoss(reduction='none')
loss = loss_f(x, y)
print("Multi Margin Loss: ", loss)
### compute by hand
x = x[0]
margin = 1
i_0 = margin - (x[1] - x[0])
# i_1 = margin - (x[1] - x[1])
i_2 = margin - (x[1] - x[2])
loss_h = (i_0 + i_2) / x.shape[0]
print(loss_h)
输出结果：
15、nn.TripletMarginLoss
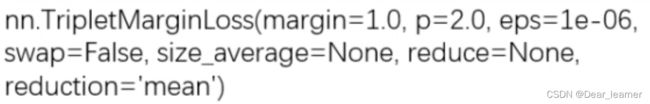
功能：计算三元组损失，人脸验证中常用
主要参数：
p：范数的阶，默认为2；
margin：边界值
reduction：计算模式，可为none/sum/mean
在人脸识别训练模型的时候，往往需要把训练集做成三元组 (A, P, N)， A 和 P 是同一个人，A 和 N 不是同一个，然后训练模型
模型把 A 和 P 看成一样的，也就是争取让 A 和 P 之间的距离小，而 A 和 N 之间的距离大，那么我们的模型就能够进行人脸识别任务了。
anchor = torch.tensor([[1.]])
pos = torch.tensor([[2.]])
neg = torch.tensor([[0.5]])
loss_f = nn.TripletMarginLoss(margin=1.0, p=1)
loss = loss_f(anchor, pos, neg)
print("Triplet Margin Loss", loss)
### compute by hand
margin = 1
a, p, n = anchor[0], pos[0], neg[0]
d_ap = torch.abs(a-p)
d_an = torch.abs(a-n)
loss = d_ap - d_an + margin
print(loss)
输出结果：
16、nn.HingeEmbeddingLoss
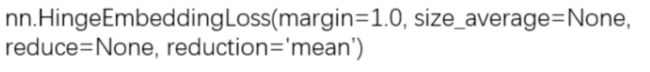
功能：计算两个输入的相似性，常用于非线性embedding和半监督学习
注意事项：输入x应为两个输入之差的绝对值
主要参数：
margin：边界值
计算公式：
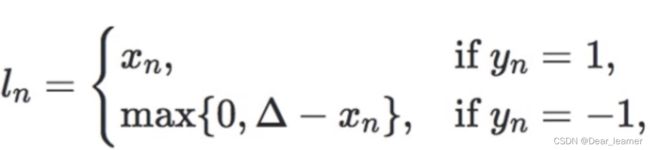
inputs = torch.tensor([[1., 0.8, 0.5]])
target = torch.tensor([[1, 1, -1]])
loss_f = nn.HingeEmbeddingLoss(margin=1, reduction='none')
loss = loss_f(inputs, target)
print("Hinge Embedding Loss", loss)
### compute by hand
margin = 1.
loss = max(0, margin - inputs.numpy()[0, 2])
print(loss)
### 输出值
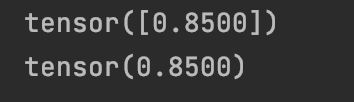
Triplet Margin Loss tensor(1.5000)
tensor([1.5000])
17、nn.CosineEmbeddingLoss
功能：采用余弦相似度计算两个输入的相似度
主要参数：
margin：边界值，可取值[-1, 1]，推荐[0, 0.5]
计算公式：
x1 = torch.tensor([[0.3, 0.5, 0.7], [0.3, 0.5, 0.7]])
x2 = torch.tensor([[0.1, 0.3, 0.5], [0.1, 0.3, 0.5]])
target = torch.tensor([[1, -1]], dtype=torch.float)
loss_f = nn.CosineEmbeddingLoss(margin=0., reduction='none')
loss = loss_f(x1, x2, target)
print("Cosine Embedding Loss", loss)
### compute by hand
margin = 0.
def cosine(a, b):
numerator = torch.dot(a, b)
denominator = torch.norm(a, 2) * torch.norm(b, 2)
return float(numerator/denominator)
l_1 = 1 - (cosine(x1[0], x2[0]))
l_2 = max(0, cosine(x1[0], x2[0]))
print(l_1, l_2)
18、nn.CTCLoss
功能：计算CTC损失，解决时序类数据的分类
主要参数：
blank：blank label
zero_infinity:无穷大的值或梯度置为0
【总结】
- 分类问题
- 二分类单标签问题：nn.BCELoss, nn.BCEWithLogitsLoss, nn.SoftMarginLoss
- 二分类多标签问题：nn.MultiLabelSoftMarginLoss
- 多分类单标签问题: nn.CrossEntropyLoss, nn.NLLLoss, nn.MultiMarginLoss
- 多分类多标签问题: nn.MultiLabelMarginLoss,
- 不常用：nn.PoissonNLLLoss, nn.KLDivLoss
- 回归问题: nn.L1Loss, nn.MSELoss, nn.SmoothL1Loss
- 时序问题：nn.CTCLoss
- 人脸识别问题：nn.TripletMarginLoss
- 半监督Embedding问题(输入之间的相似性): nn.MarginRankingLoss, nn.HingeEmbeddingLoss, nn.CosineEmbeddingLoss