动态规划问题
目录
一、动态规划简介
二、利用动态规划解决问题
1、斐波拉契序列
2、拆分词句
3、三角形最小路径和
4、不同的路径数目(一)
5、带权值的最小路径和
6、求路径ii
7、01背包
8、不同子序列
9、编辑距离
10、分割回文串
一、动态规划简介
动态规划就是分治思想的延伸,通俗来讲就是大事化小,小事化了。
在将大问题划分为小问题的分治过程中,将小问题的处理结果进行保存以便后面处理大问题时使用到这些结果。
动态规划具有三个特点:
- 将原来的问题分解成几个相似的子问题。
- 所有的子问题只需要解决一次。
- 存储子问题的解。
动态规划的本质:状态的定义和状态方程的定义。
动态规划问题的四个要素:
- 状态的定义。
- 状态间的转移方程的定义。
- 状态的初始化。
- 返回结果。
定义的状态之间要形成递推关系。
动态规划问题的使用场景:求最值、可不可行、是不是、求方案的个数。
二、利用动态规划解决问题
1、斐波拉契序列
题目链接:斐波拉契数列
大家都知道斐波那契数列,现在要求输入一个正整数 n ,请你输出斐波那契数列的第 n 项。
题目分析:
- 状态的定义:F(i) 表示斐波拉契数列的第i项。
- 状态间的转移方程:F(i) = F(i-1)+F(i-2)。
- 初始化:F(1) = 1,F(2) = 1。
- 返回值:F(n)。
代码实现:
public int Fibonacci(int n) {
int[] fib = new int[n+1];
fib[1] = 1;
fib[2] = 1;
for(int i = 3;i <= n;i++){
fib[i] = fib[i-1] + fib[i-2];
}
return fib[n];
}
2、拆分词句
题目链接:拆分词句
给定一个字符串s和一组单词dict,判断s是否可以用空格分割成一个单词序列,使得单词序列中所有的单词都是dict中的单词(序列可以包含一个或多个单词)。
例如:
给定s=“nowcode”;
dict=["now", "code"].
返回true,因为"nowcode"可以被分割成"now code".
题目分析:
要判断分割的单词序列是否都是dict中的单词,因为分割是从前往后进行分割,那么我们就可以给每个字符设置出一个状态true表示可以分割,如果子状态canSplit[j]为true,也就是前面一部分在dict中,那么判断后面j~i是否为dict中的元素,如果是就将canSplit[i]置为true继续向后判断,由于要判断这个s分割的单词都在dict中,所以就创建canSplit数组时需要增加一个元素canSplit[s.length()]来表示,还有一个特殊情况:如果仅仅分割s的第一个字符为dict中的元素,那么其子问题的状态怎么设定?所以就将canSplit[0]=true,表示0下标之前的状态为true,综上利用动态规划可以分析出:
- 状态的定义 :canSplit[i]:表示该字符对应的下标是否可以拆分
- 状态间转移方程的定义:j
- 状态初始化:canSplit[0]=true
- 返回结果:canSplit[字符串长度]的状态,表示整个字符串分割的单词是都在dict中。
代码实现:
public boolean wordBreak(String s, Set dict) {
if(s == null || dict == null){
return false;
}
boolean[] canSplit = new boolean[s.length()+1];
canSplit[0] = true;
for(int i = 1;i <= s.length();i++){
for(int j = 0;j < i;j++){
if(canSplit[j]&&dict.contains(s.substring(j,i))){
canSplit[i] = true;
}
}
}
return canSplit[s.length()];
} 3、三角形最小路径和
题目链接:三角形最小路径和
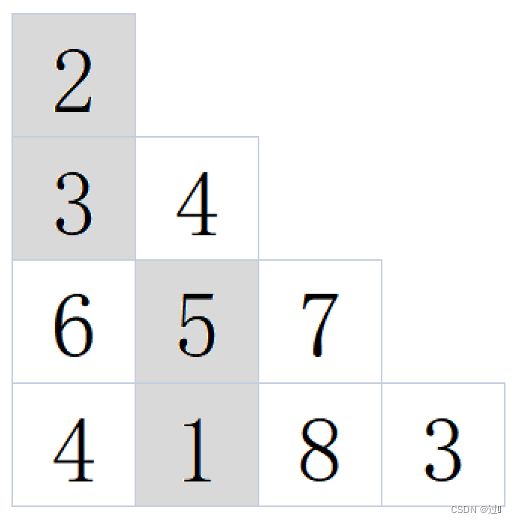
给定一个正三角形数组,自顶到底分别有 1,2,3,4,5...,n 个元素,找出自顶向下的最小路径和。每一步只能移动到下一行的相邻节点上,相邻节点指下行种下标与之相同或下标加一的两个节点。
例如当输入[[2],[3,4],[6,5,7],[4,1,8,3]]时,对应的输出为11,
所选的路径如下图所示:
题目分析:
要求从三角形的顶点到底部的最小路径,那么就需要求出其上层的最小路径,假设F(i,j)表示到结点的最小路径,如果该结点是最短路径上的点就直接将该点的值修改为顶点到该点的最小路径和,就不用再开辟新的空间了,又由于每一步只能移动到下一行的相邻节点上,所以结点(i,j)的最短路径F(i,j)=min(F(i-1,j)+F(i-1,j-1)),但是对于三角形两个边上的点其上层的最小路径只需加上其上层的一个点:如果j=0,F(i,j)=F(i-1,j);如果i=j,F(i,j)=F(i-1,j),于是就利用动态规划分析得出:
- 状态的定义:F(i,j):到结点(i,j)的最小路径和(包含结点(i,j)的值)
- 状态间转移方程的定义:F(i,j)=min(F(i-1,j)+F(i-1,j-1)),如果j=0,F(i,j)=F(i-1,j);如果i=j,F(i,j)=F(i-1,j)
- 状态初始化:F(0,0)=val((0,0)结点的值)
- 返回值:min(F(底部结点))
代码实现:
public int minTrace (int[][] triangle) {
if(triangle == null){
return 0;
}
int row = triangle.length;
for(int i = 1;i < row;i++){
for(int j = 0;j <= i;j++){
if(j == 0){
triangle[i][j] += triangle[i-1][j];
}else if( j == i){
triangle[i][j] += triangle[i-1][j-1];
}else{
triangle[i][j] += Math.min(triangle[i-1][j-1],triangle[i-1][j]);
}
}
}
int min=triangle[row-1][0];
for(int i = 1;i < triangle[row - 1].length;i++){
if(triangle[row - 1][i] < min){
min = triangle[row -1][i];
}
}
return min;
}上述思路是从顶点到点(i,j)的最短路径,那么也可以从点(i.j)到顶点的最短路径,就从倒数第二层开始遍历,那么利用动态规划分析可得:
- 状态的定义:F(i,j) 为底部到点(i,j)的最短路径。
- 状态间转移方程的定义:F(i,j)=min(F(i+1,j)+F(i+1,j+1))。
- 状态初始化:F(i,j)=triangle(i,j)。
- 返回值:F(0,0)。
代码实现:
public int minTrace (int[][] triangle) {
if(triangle == null){
return 0;
}
int rows = triangle.length;
for(int i = rows - 2;i >= 0;i--){
for(int j = 0; j <= i;j++){
triangle[i][j] += Math.min(triangle[i+1][j+1],triangle[i+1][j]);
}
}
return triangle[0][0];
}4、不同的路径数目(一)
题目链接:不同的路径数目(一)
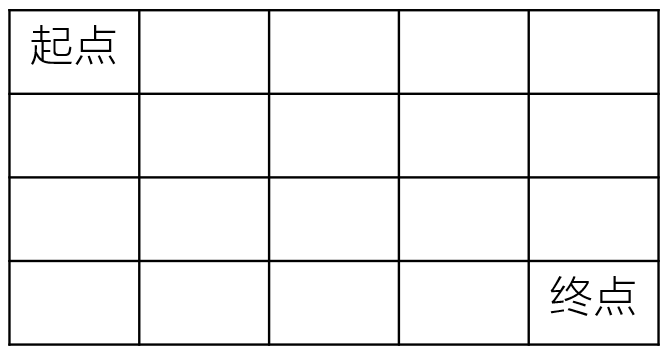
一个机器人在m×n大小的地图的左上角(起点)。
机器人每次可以向下或向右移动。机器人要到达地图的右下角(终点)。
可以有多少种不同的路径从起点走到终点?
备注:m和n小于等于100,并保证计算结果在int范围内
题目分析:
由于机器人每次可以向下或向右移动,对于到达第一行和第一列的点只有一种路径,经过分析到达其他点的路径方案为左边点的路径方案数和上边点的路径方案数之和。所以利用动态规划分析如下:
- 状态的定义:F(i,j)表示起点到点(i,j)的路径方案数。
- 状态间的转移方程:F(i,j) = F(i-1,j) + F(i,j-1)。
- 状态初始化:F(i,1)=1,F(i,j)=1,到达第一行和第一列的点只有一种路径。
- 返回值:F(m,n)。
代码实现:
public int uniquePaths (int m, int n) {
int[][] path = new int[m+1][n+1];
for(int i = 1; i <= n;i++){
path[1][i] = 1;
}
for(int i = 1; i <= m;i++){
path[i][1] = 1;
}
for(int i = 2; i <= m;i++){
for(int j = 2;j <= n;j++){
path[i][j] = path[i][j-1] + path[i-1][j];
}
}
return path[m][n];
}5、带权值的最小路径和
题目链接:带权值的最小路径和
给定一个由非负整数填充的m x n的二维数组,现在要从二维数组的左上角走到右下角,请找出路径上的所有数字之和最小的路径。
注意:你每次只能向下或向右移动。
题目分析:
利用动态规划分析如下:
- 状态的定义:F(i,j)表示起点到坐标为(i,j)的最小路径和。
- 状态间的转移方程:F(i,j) = min(F(i-1,j), F(i,j-1))。
- 状态初始化:F(i,0) +=F(i-1,0);F(0,j) +=F(0,j-1)第一行和第一列元素进行初始化。
- 返回值:F(m-1,n-1)。
代码实现:
public int minPathSum (int[][] grid) {
int rows = grid.length;
int cols = grid[0].length;
for(int i = 1; i < rows;i++){
grid[i][0] += grid[i-1][0];
}
for(int i = 1; i < cols;i++){
grid[0][i] += grid[0][i-1];
}
for(int i = 1; i < rows;i++){
for(int j =1;j < cols;j++){
grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]);
}
}
return grid[rows-1][cols-1];
}6、求路径ii
题目链接:求路径ii
给定一个m*n的地图,其中加入了一些障碍。每次只能向下或者向右走,问从左上角走到右下角有多少不同的路径?
分别用0和1代表空区域和障碍
例如
下图表示有一个障碍在3*3的图中央。
[ [0,0,0], [0,1,0], [0,0,0] ]有2条不同的路径
备注:m和n不超过100.
题目分析:
由动态规划思想分析可得:
- 状态的定义:F(i,j)表示起点到点(i,j)的路径方案数。
- 状态间的转移方程:如果obstacleGrid(i,j)=1,F(i,j)=0,否则F(i,j)=F(i-1,j)(j=0),F(i,j)=F(i,j-1)(i=0),F(i,j) = F(i-1,j) + F(i,j-1)(i!=0,j!=0)。
- 状态初始化:F(0,0)=obstacleGrid(0,0)==1?0:1。
- 返回值:F(m-1,n-1)。
代码实现:
public static int uniquePathsWithObstacles (int[][] obstacleGrid) {
if(obstacleGrid==null)
return 0;
int i,j;
int m=obstacleGrid.length;
int n=obstacleGrid[0].length;
int[][]f=new int[m][n];
if(obstacleGrid[0][0]==1){
return 0;
}
else{
f[0][0]=1;
}
for(i=0;i7、01背包
题目链接:01背包
已知一个背包最多能容纳体积之和为v的物品,现有 n 个物品,第 i 个物品的体积为 vi , 重量为 wi,求当前背包最多能装多大重量的物品?
题目分析:
- 状态的定义:F(i,j)表示i个物品和体积为j的重量。
- 状态间的转换方程: 如果空间不足,F(i,j) = F(i-1,j).如果空间充足就要判断是否放入元素取max( F(i-1,j),(F(i-1,j-vi)+wi))。
- 初始化:第0行和第0列的元素为0,表示未放任何物品和体积为0的情况。
- 返回值:F(m,n)。
代码实现:
/**
* 计算01背包问题的结果
* @param V int整型 背包的体积
* @param n int整型 物品的个数
* @param vw int整型二维数组 第一维度为n,第二维度为2的二维数组,vw[i][0],vw[i][1]分别描述i+1个物品的vi,wi
* @return int整型
*/
public static int knapsack (int V, int n, int[][] vw) {
int[][] maxValue = new int[n+1][V+1];
for(int i = 1; i <= n;i++){
for(int j = 1; j <= V;j++){
if(j < vw[i-1][0]){
maxValue[i][j] = maxValue[i-1][j];
}else{
maxValue[i][j] = Math.max(maxValue[i-1][j],maxValue[i-1][j-vw[i-1][0]]+vw[i-1][1]);
}
}
}
return maxValue[n][V];
}8、不同子序列
题目链接:不同的子序列
给定两个字符串S和T,返回S子序列等于T的不同子序列个数有多少个?
字符串的子序列是由原来的字符串删除一些字符(也可以不删除)在不改变相对位置的情况下的剩余字符(例如,"ACE"is a subsequence of"ABCDE"但是"AEC"不是)
例如:S="nowcccoder", T = "nowccoder"
返回3
题目分析:
- 状态的定义:dp[i][j]表示以i-1结尾的字符串S等于以j-1结尾的字符串T子序列的个数。
- 状态间的转移方程:dp[i][j]=(S[i-1]==T[j-1])?(dp[i-1][j-1]+dp[i-1][j]):dp[i-1][j].
- 初始化:dp[0][j] = 0,表示S字符串为空,dp[i][0] = 1,表示T字符串为空,dp[0][0]=1表示S和T都为空。
- 返回值:dp[S.length()][T.length()]。
代码实现:
public int numDistinct (String S, String T) {
int lenS = S.length();
int lenT = T.length();
int[][] dp = new int[lenS+1][lenT+1];
for(int i = 0;i <= lenS;i++){
dp[i][0] = 1;
}
for(int i = 1;i <= lenS;i++){
for(int j = 1;j <= lenT;j++){
if(S.charAt(i-1) == T.charAt(j-1)){
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
}else{
dp[i][j] = dp[i-1][j];
}
}
}
return dp[lenS][lenT];
}9、编辑距离
题目链接:编辑距离
给定两个单词word1和word2,请计算将word1转换为word2至少需要多少步操作。
你可以对一个单词执行以下3种操作:
a)在单词中插入一个字符
b)删除单词中的一个字符
c)替换单词中的一个字符
题目分析:
- 状态的定义:dp[i][j]表示前i-1的word1转换为前j-1的word2需要多少步操作。
- 状态间的转换方程:dp[i][j]=(word1[i-1]==word2[j-1])?dp[i-1][j-1]:(min(dp[i-1][j]+1, dp[i][j-1]+1,dp[i-1][j-1]+1),dp[i-1][j]+1表示删除word1的第i-1个字符,dp[i][j-1]+1表示新增word1的第i-1个字符,dp[i-1][j-1]+1表示替换word1的第i-1个字符。
- 初始化:dp[0][0] = 0,dp[0][j] = j,dp[i][0] = i。
- 返回值:p[word1.length()][word2.length()]。
代码实现:
public int minDistance (String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] dp = new int[len1+1][len2+1];
for(int i = 1;i <= len1;i++){
dp[i][0] = i;
}
for(int j = 1;j <= len2;j++){
dp[0][j] = j;
}
for(int i = 1;i <= len1;i++){
for(int j = 1;j <= len2;j++){
if(word1.charAt(i-1) == word2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}else{
int min1 = Math.min(dp[i-1][j-1],dp[i-1][j]);
int min2 = Math.min(dp[i][j-1],dp[i-1][j]);
dp[i][j] = Math.min(min1,min2) + 1;
}
}
}
return dp[len1][len2];
}10、分割回文串
题目链接:分割回文串
给出一个字符串s,分割s使得分割出的每一个子串都是回文串
计算将字符串s分割成回文分割结果的最小切割数
例如:给定字符串s="aab",
返回1,因为回文分割结果["aa","b"]是切割一次生成的。
题目分析:
- 状态的定义:dp[i]表示到第i个字符分割的次数。
- 状态间的转移方程:dp[i] = min(dp[i],dp[j]+1)。
- 初始化:dp[i]表示到第i个字符的最大分割次数。
- 返回值:dp[s.length()]。
public boolean isPalindrome(String s){
int begin = 0;
int end = s.length()-1;
while(begin < end){
if(s.charAt(begin) == s.charAt(end)){
begin++;
end--;
}else{
return false;
}
}
return true;
}
public int minCut (String s) {
int len = s.length();
int[] dp = new int[len+1];
for(int i = 0;i <= len;i++){
dp[i] = i-1;
}
for(int i = 1;i <= len;i++){
for(int j = 0;j