【LeetCode学习计划】《数据结构入门-C++》第14天 树

LeetCode【学习计划】：【数据结构】

---

---

98. 验证二叉搜索树

LeetCode: 98. 验证二叉搜索树

$中等$

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

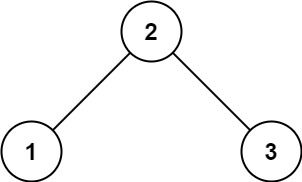
输入：root = [2,1,3]
输出：true

示例 2：

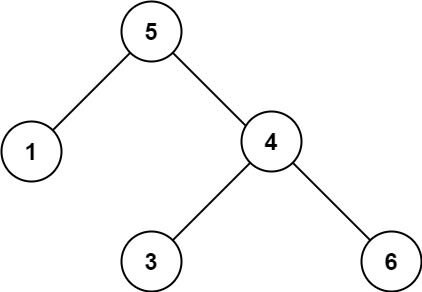
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 10⁴] 内
• -2³¹ <= Node.val <= 2³¹ - 1

---

方法1：中序遍历

中序遍历的顺序为：左孩子->根节点->右孩子，因此二叉搜索树的中序遍历结果正好是升序的。我们可以结合 [第10天] 的代码来完成。

首先定义一个 last 变量作为最小值。每次遍历一个结点时，将它的值与 last 进行比较，如果小于等于 last，那就说明遍历结果不是升序，树也不是一棵二叉搜索树，返回假值。最后，将当前结点的值赋给 last，留给后面一个结点去比较。

需要注意的是：本题中结点的值的范围为 [-2³¹, 2³¹ - 1]，正好是C++中 int 整型的完整范围。所以 last 变量的最小值必须比 int 所能表示的最小值还要小，因此 last 的类型可以是 long long，而初值只要比 -2³¹ 即可。

#include 
using namespace std;
class Solution
{
public:
    bool isValidBST(TreeNode *root)
    {
        stack<TreeNode *> stk;
        long long last = (long long)INT_MIN - 1;

        TreeNode *p = root;
        while (!stk.empty() || p)
        {
            while (p)
            {
                stk.push(p);
                p = p->left;
            }
            p = stk.top();
            stk.pop();
            if (p->val <= last)
                return false;

            last = p->val;
            p = p->right;
        }
        return true;
    }
};

复杂度分析

• 时间复杂度：$O(n)$。n 为树中的结点数，每个结点都要遍历一次。

• 空间复杂度：$O(n)$。主要为栈的开销。

参考结果

Accepted
80/80 cases passed (16 ms)
Your runtime beats 38.39 % of cpp submissions
Your memory usage beats 55.77 % of cpp submissions (21.1 MB)

---

方法2：递归

二叉搜索树中，根结点的左孩子比根结点小，同时左子树上的所有结点比根结点小，也意味着根节点的值成为了左子树的值上限。左孩子也是它自身的左子树的值上限。同理，根节点的值是右子树的值下限。所以我们在递归时维护每一个结点的上下限即可，如果结点的值不在上下限中（开区间）则不是二叉搜索树。

#include 
class Solution
{
public:
    bool isValidBST(TreeNode *root)
    {
        return isValidSubBST(root, LONG_MIN, LONG_MAX);
    }
    bool isValidSubBST(TreeNode *root, long long lower, long long upper)
    {
        if (!root)
            return true;
        if (root->val <= lower || root->val >= upper)
            return false;
        return isValidSubBST(root->left, lower, root->val) && isValidSubBST(root->right, root->val, upper);
    }
};

复杂度分析

• 时间复杂度：$O(n)$

• 空间复杂度：$O(n)$。空间复杂度和递归深度有关。

参考结果

Accepted
80/80 cases passed (0 ms)
Your runtime beats 100 % of cpp submissions
Your memory usage beats 70.13 % of cpp submissions (21.1 MB)

---

---

653. 两数之和 IV - 输入 BST

LeetCode: 653. 两数之和 IV - 输入 BST

$简单$

给定一个二叉搜索树 root 和一个目标结果 k，如果 BST 中存在两个元素且它们的和等于给定的目标结果，则返回 true。

示例 1：

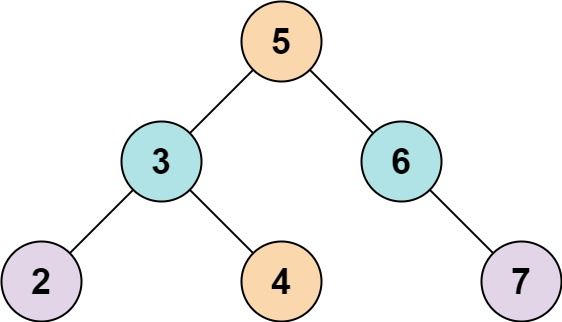
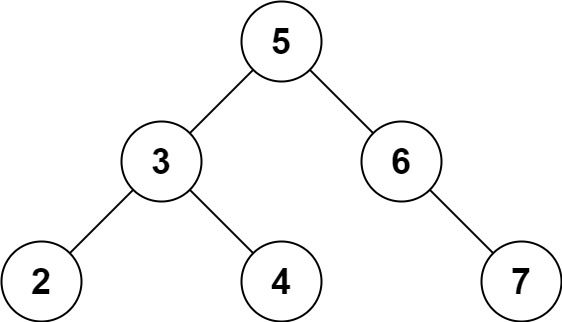
输入: root = [5,3,6,2,4,null,7], k = 9
输出: true

示例 2：

输入: root = [5,3,6,2,4,null,7], k = 28
输出: false

示例 3：

输入: root = [2,1,3], k = 4
输出: true

示例 4：

输入: root = [2,1,3], k = 1
输出: false

示例 5：

输入: root = [2,1,3], k = 3
输出: true

提示:

• 二叉树的节点个数的范围是 [1, 10⁴].
• -10⁴ <= Node.val <= 10⁴
• root 为二叉搜索树
• -10⁵ <= k <= 10⁵

---

方法1：中序遍历 + 双指针

在上文的 98. 验证二叉搜索树 一题中，我们知道了二叉搜索树的中序遍历结果是升序的，所以我们可以中序遍历整棵树然后将结果存入一个数组中。

得到升序数组后，我们可以像 【LeetCode学习计划】《算法-入门-C++》第3天 双指针 一文中 167. 两数之和 II - 输入有序数组 一题，确定一个值 num 然后用二分查找搜索 target-num，或者是使用双指针查找，这里我们就选择双指针。

#include 
#include 
using namespace std;
class Solution
{
public:
    bool findTarget(TreeNode *root, int k)
    {
        stack<TreeNode *> stk;
        TreeNode *p = root;
        vector<int> nums;
        while (p || !stk.empty())
        {
            while (p)
            {
                stk.push(p);
                p = p->left;
            }
            p = stk.top();
            stk.pop();

            nums.emplace_back(p->val);

            p = p->right;
        }

        for (int left = 0, right = nums.size() - 1; left < right;)
        {
            int sum = nums[left] + nums[right];
            if (sum == k)
                return true;
            else if (sum < k)
                left++;
            else
                right--;
        }
        return false;
    }
};

复杂度分析

• 时间复杂度：$O(n)$。n 为树中的结点数。中序遍历的时间复杂度为$O(n)$，双指针部分的时间复杂度为$O(n)$，所以总时间复杂度为$O(2n)=O(n)$。

• 空间复杂度：$O(n)$。主要是栈和数组的开销，空间复杂度为$O(2n)=O(n)$。

参考结果

Accepted
422/422 cases passed (32 ms)
Your runtime beats 85.11 % of cpp submissions
Your memory usage beats 55.07 % of cpp submissions (36.1 MB)

---

---

235. 二叉搜索树的最近公共祖先

LeetCode: 235. 二叉搜索树的最近公共祖先

$简单$

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
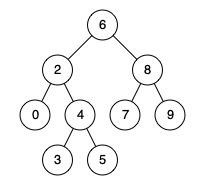
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

---

方法1：两次查找

题目保证目标结点存在于给定的二叉搜索树中，因此我们可以参考 【LeetCode学习计划】《数据结构入门-C++》第13天 树 中的 700. 二叉搜索树中的搜索 一题，先在二叉搜索树中查找目标结点。查找的过程中，将路径存入数组中。

2个结点的路径获得后，从头开始遍历数组，当2个数组中对应的结点不同时，就代表遇到了分岔路。2个结点的最近公共祖先就是数组中的上一个结点。

#include 
using namespace std;
class Solution
{
public:
    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
    {
        vector<TreeNode *> path1 = searchBSTPath(root, p->val);
        vector<TreeNode *> path2 = searchBSTPath(root, q->val);

        TreeNode *ancestor = nullptr;
        for (auto it1 = path1.begin(), it2 = path2.begin(); it1 != path1.end() && it2 != path2.end(); it1++, it2++)
        {
            if (*it1 == *it2)
            {
                ancestor = *it1;
            }
            else
                break;
        }
        return ancestor;
    }
    vector<TreeNode *> searchBSTPath(TreeNode *root, int val)
    {
        vector<TreeNode *> path;
        TreeNode *p = root;
        while (p)
        {
            path.push_back(p);
            if (p->val == val)
                break;
            p = val < p->val ? p->left : p->right;
        }
        return path;
    }
};

复杂度分析

• 时间复杂度：$O(n)$

• 空间复杂度：$O(n)$。主要为路径数组的开销。

参考结果

Accepted
27/27 cases passed (28 ms)
Your runtime beats 71.62 % of cpp submissions
Your memory usage beats 45.14 % of cpp submissions (22.8 MB)

---

方法2：一次查找

由方法1中可以知道，两个结点 p 和 q 的路径中，前面1至多个结点都是相同的，后面的0至多个结点是不同的。这也就代表着，如果同时对 p 和 q 进行查找，在相同的路径中，它们会同时往左往右走，也就是说它们都小于或大于当时的根节点。如果不能同时地大于小于，就说明遇到了分岔路，而当时的根结点就是它们的最近公共祖先。

#include 
using namespace std;
class Solution
{
public:
    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
    {
        TreeNode *ancestor = root;
        while (true)
        {
            if (p->val < ancestor->val && q->val < ancestor->val)
            {
                ancestor = ancestor->left;
            }
            else if (p->val > ancestor->val && q->val > ancestor->val)
            {
                ancestor = ancestor->right;
            }
            else
                break;
        }
        return ancestor;
    }
};

复杂度分析

• 时间复杂度：$O(n)$

• 空间复杂度：$O(1)$。没有用到额外空间。

参考结果

Accepted
27/27 cases passed (20 ms)
Your runtime beats 98.38 % of cpp submissions
Your memory usage beats 45.14 % of cpp submissions (22.8 MB)