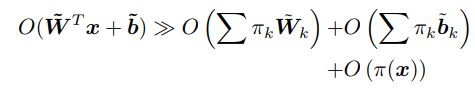(二)动态卷积之Dynamic Convolution
代码地址:code
论文题目:Dynamic Convolution: Attention over Convolution Kernels
论文地址:paper
目录
前言
Dynamic Convolution解决的问题
动态感知机
Dynamic Convolution结构
实验结果
Dynamic Convolution代码实现(Pytorch)
参考
前言
动态卷积
现在的诸多task中,普遍需要capacity较大的模型,而随着模型参数的不断增加,计算成本也越来越高。对于一些对latency有较高要求的task,显然是一种挑战。在传统的CNN网络中,一旦训练完成,所有的kernal参数就固定了。对于任意的输入,所有的kernal都对他们同等对待。所以为了提高模型的capacity,大多数方法堆叠卷积层或者增加卷积层的channel数(即增加深度和广度),这种做法虽然一定程度上可以提升模型performance,但显然会造成 computationally expensive。
所以为了压缩模型,在增加模型capacity的同时不会增加太多参数和计算量,动态卷积的概念应运而生。动态卷积的出发点就是,当训练结束后,kernal不再是一个定值,而是一个由input决定的变量。因此kernal相当于一个以input为自变量的function;换句话说就是对于不同的input,都会通过计算得到各自不同的卷积核参数。这种做法相当于变相的增加了模型的capacity,与此同时模型参数和计算量是非常小的。
Dynamic Convolution解决的问题
轻量级卷积神经网络(light-weight convolutional neural network)因其较低的计算预算而限制了 CNN 的深度(卷积层数)和宽度(通道数),不仅导致模型性能下降,表示能力也会受到限制。为了解决这个问题,微软的研究员们提出了动态卷积,这种新的设计能够在不增加网络深度或宽度的情况下增加模型的表达能力(representation capacity)。动态卷积的基本思路就是根据输入图像,自适应地调整卷积参数。(所得卷积核与输入相关,即不同数据具有不同的卷积,这也就是动态卷积的由来。)
动态感知机
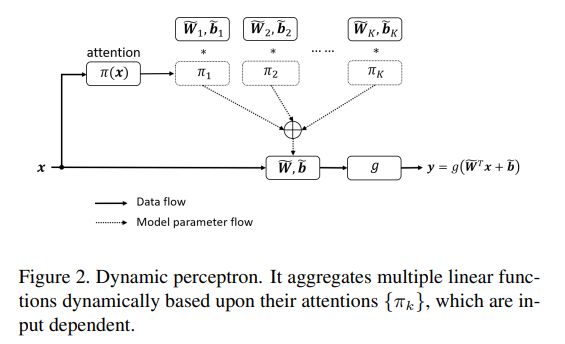
作者通过感知器模型引出了动态卷积,我们设感知器模型如下图,W,b,g分别表示权重,偏置和激活函数.
动态感知器的定义如下图,动态感知器模型如y式,它的权值和偏置分别是通过W式和b式中多个权值和偏置通过加权求和得到的,最后一个公式表示对权值系数的约束这里权值系数不是固定的,而是随着输入数据的变化而变化,具有更强的特征表达能力.动态卷积Dynamic Convolution和动态感知器中W和b计算一样.
其中![]() 表示第k个线性函数
表示第k个线性函数![]() 的attetion权重,这个权重在输入x 不同的情况下是不同的。因此在给定input的情况下,动态感知器代表了该input的最佳线性函数组合。又因为该模型是非线性的,所以动态感知器拥有更强大的representation能力。
的attetion权重,这个权重在输入x 不同的情况下是不同的。因此在给定input的情况下,动态感知器代表了该input的最佳线性函数组合。又因为该模型是非线性的,所以动态感知器拥有更强大的representation能力。
动态感知器的图解如下图所示,和上图公式表达是吻合的.
作者也指出:相比静态感知器,动态感知器需要两个额外的计算:(a)注意力权值计算;(2)动态权值融合。尽管如此,这两点额外计算相比感知器的计算量可以忽略:
Dynamic Convolution结构
动态卷积DynamicConv,其实和动态感知器的思想是非常相似的
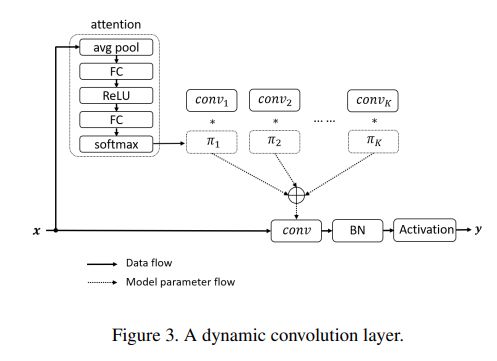
就是原本的一个固定的卷积核,现在变为可以根据输入自适应改变注意力的卷积核。如上图所示,现在一个卷积核由K个卷积核决定,参数量大约上升了K倍(论文中说计算量并没有上升多少)
输入经过注意力提取,得到这k个卷积核的权重,线性加权起来就是新的一个卷积核。
给某个Layer设置K 个尺度和通道数相同的kernal,通过各自的attention权重![]() 进行融合,从而得到该层的卷积核参数。计算
进行融合,从而得到该层的卷积核参数。计算![]() (x)的过程如图中虚线方框所示,首先做GlobalAvgPooling,得到全局Spatial特征,再通过两个FC层映射到K 的维度,最后做softmax归一化。这样得到的K个attention权重就可以分配给该层的K个kernal。这里与SENet不同的是,SENet是在channel层面的attention,而DynamicConv是以整个kernal为一个被attention的对象。
(x)的过程如图中虚线方框所示,首先做GlobalAvgPooling,得到全局Spatial特征,再通过两个FC层映射到K 的维度,最后做softmax归一化。这样得到的K个attention权重就可以分配给该层的K个kernal。这里与SENet不同的是,SENet是在channel层面的attention,而DynamicConv是以整个kernal为一个被attention的对象。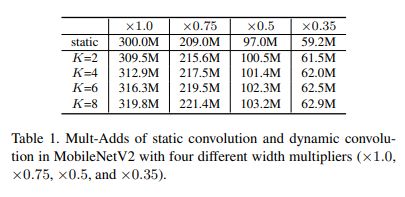
再关注一下计算复杂度:假设feature map的大小为H ∗ W ,kernal的size为![]() ,
,![]() 和
和![]() 表示输入通道数和输出通道数。所以在计算attention权重时额外增加的计算量为
表示输入通道数和输出通道数。所以在计算attention权重时额外增加的计算量为![]() (除以4是因为第一层FC将维度从
(除以4是因为第一层FC将维度从![]() 缩小到四分之一),在kernal融合时额外增加的计算量为
缩小到四分之一),在kernal融合时额外增加的计算量为![]() 。这两部分额外开销都远小于静态卷积计算的
。这两部分额外开销都远小于静态卷积计算的![]() ,因此只要当K < < H W ,这部分额外开销是非常efficient的,根据上表可以直观看出。
,因此只要当K < < H W ,这部分额外开销是非常efficient的,根据上表可以直观看出。
训练过程中要关注两个问题:(1)通过softmax把所有的attention weight限定在[0,1]内,并且sum为1。这样做就把kernal融合的空间压缩为一个三角形空间,相比于CondConv的两个pyramid空间,更适合进行优化;(2)由于attention权重大多数是sparse的(与CondConv的实验异曲同工),所以大多数的kernal得不到训练,为解决这个问题,作者提出了下述公式进行平滑:
这里![]() 表示第二层FC的输出。举个栗子方便理解:假设该层有K=2个kernal,z zz输出的结果为(0.01, 0.99),那么在反向传播时第二个kernal可以得到更好地学习,而第一个kernal的参数学习会被抑制。所以采用上述公式,假如超参数
表示第二层FC的输出。举个栗子方便理解:假设该层有K=2个kernal,z zz输出的结果为(0.01, 0.99),那么在反向传播时第二个kernal可以得到更好地学习,而第一个kernal的参数学习会被抑制。所以采用上述公式,假如超参数![]() ,那么此时
,那么此时![]() 的值就比之前不做平滑的大很多。因为
的值就比之前不做平滑的大很多。因为![]() 即使缩小了30被,经指数函数仍然是趋近于1;而
即使缩小了30被,经指数函数仍然是趋近于1;而![]() 一旦缩小30倍,attention就从
一旦缩小30倍,attention就从![]() 下降成了
下降成了![]() ,这个削弱幅度是巨大的。因此平滑操作有利于所有的kernel进行参数的迭代更新。
,这个削弱幅度是巨大的。因此平滑操作有利于所有的kernel进行参数的迭代更新。
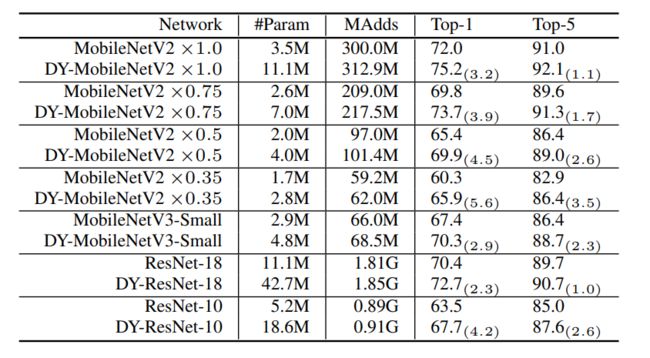
实验结果
将经典卷积网络中传统卷积替换为Dynamic Convolution前后实验对比:
Dynamic Convolution代码实现(Pytorch)
GAP代码实现:
class attention2d(nn.Module):
def __init__(self, in_planes, K,):
super(attention2d, self).__init__()
self.avgpool = nn.AdaptiveAvgPool2d(1)
self.fc1 = nn.Conv2d(in_planes, K, 1,)
self.fc2 = nn.Conv2d(K, K, 1,)
def forward(self, x):
x = self.avgpool(x)
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x).view(x.size(0), -1)
return F.softmax(x, 1)Dynamic Convolution代码实现
class Dynamic_conv2d(nn.Module):
def __init__(self, in_planes, out_planes, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, K=4,):
super(Dynamic_conv2d, self).__init__()
assert in_planes%groups==0
self.in_planes = in_planes
self.out_planes = out_planes
self.kernel_size = kernel_size
self.stride = stride
self.padding = padding
self.dilation = dilation
self.groups = groups
self.bias = bias
self.K = K
self.attention = attention2d(in_planes, K, )
self.weight = nn.Parameter(torch.Tensor(K, out_planes, in_planes//groups, kernel_size, kernel_size), requires_grad=True)
if bias:
self.bias = nn.Parameter(torch.Tensor(K, out_planes))
else:
self.bias = None
def forward(self, x):#将batch视作维度变量,进行组卷积,因为组卷积的权重是不同的,动态卷积的权重也是不同的
softmax_attention = self.attention(x)
batch_size, in_planes, height, width = x.size()
x = x.view(1, -1, height, width)# 变化成一个维度进行组卷积
weight = self.weight.view(self.K, -1)
# 动态卷积的权重的生成, 生成的是batch_size个卷积参数(每个参数不同)
aggregate_weight = torch.mm(softmax_attention, weight).view(self.out_planes, -1, self.kernel_size, self.kernel_size)
if self.bias is not None:
aggregate_bias = torch.mm(softmax_attention, self.bias).view(-1)
output = F.conv2d(x, weight=aggregate_weight, bias=aggregate_bias, stride=self.stride, padding=self.padding,
dilation=self.dilation, groups=self.groups*batch_size)
else:
output = F.conv2d(x, weight=aggregate_weight, bias=None, stride=self.stride, padding=self.padding,
dilation=self.dilation, groups=self.groups * batch_size)
output = output.view(batch_size, self.out_planes, output.size(-2), output.size(-1))
return output参考
动态卷积之CondConv和DynamicConv_汐梦聆海的博客-CSDN博客_动态卷积