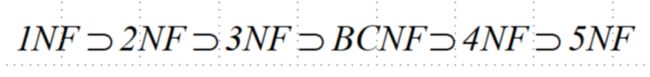![]()
本节其实就干了两件事情 :
- 首先讨论一个关系属性间不同的依赖情况,讨论如何根据属性间依赖情况来判定关系是否具有某些不合适的性质
- 通常按属性间依赖情况来区分关系规范化程度为第一范式、第二范式、第三范式和第四范式等,然后直观地描述如何将具有不合适性质的关系转换为更合适的形式
一:函数依赖
(1)函数依赖
函数依赖:简单点说就是,如果X能确定Y(或者说Y依赖X,记作X->Y)那么就不可能存在两个元组,在X相同时Y却不同
如下在Student关系中,Sno确定Sdept,所以不可能出现两个相同的Sno却对应不同的Sdept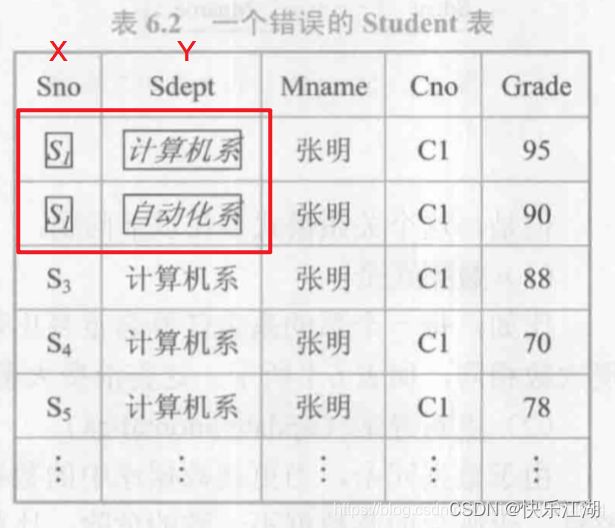
(2)平凡函数依赖与非平凡函数依赖
平凡函数依赖与非平凡函数依赖:
- 非平凡函数依赖:如果X确定Y,但Y并不是X的子集,那么则称X是Y的非平凡函数依赖
- 平凡函数依赖:如果X确定Y,Y是X的子集,那么则称X是Y的平凡函数依赖
(3)完全函数依赖与部分函数依赖
完全函数依赖与部分函数依赖:
- 完全函数依赖:要想X是Y完全函数依赖,那么X中任何一个分量都不能丢,哪怕少一个,X都无法确定Y
- 部分函数依赖:X是Y的部分函数依赖,则表明即便去掉X中的一个或多个分量,剩余分量也能确定Y
如下是一个经典例子
(4)传递函数依赖
传递函数依赖:如果X是Y的非平凡函数依赖,且Y不是X的函数依赖,同时Y是Z的非平凡函数依赖,则称Z对X传递函数依赖,记作
- 注意,如果Y是X的函数依赖,则称Z直接依赖于X
如下是一个经典例子
二:多值依赖(此部分内容看过BCNF之前再看)
(1)多值依赖的例子
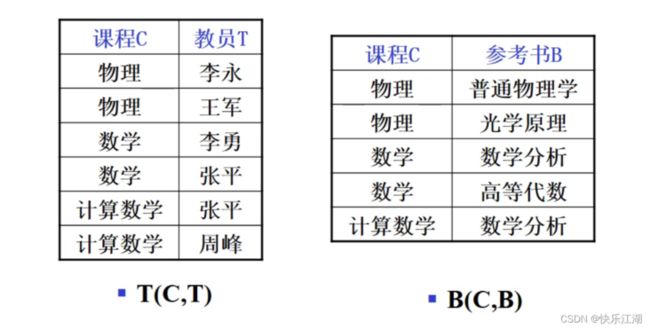
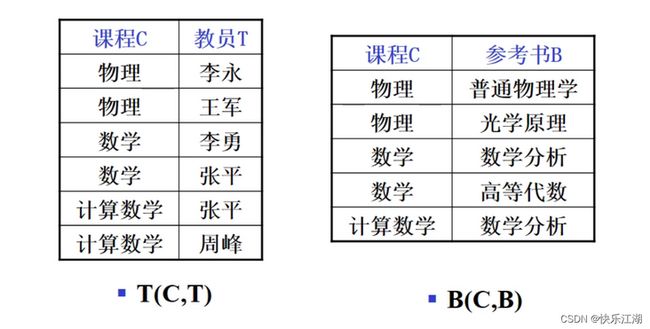
【例】学校中某一门课程由多个教师讲授,他们使用相同的一参考书。每个教师可以讲授多门课程,每种参考书可以供多门课程使用。可以用一个非规范化的关系来表示教师T、课程C和参考书B之间的关系

把这张表变成一张规范化的二维表
关系模型Teaching(C,T,B)的码是全码,也即所有属性组都是候选码,或者只有一个候选码
这样的关系会产生下面的一些问题
- 插入异常:例如,某一课程(如物理)增加一名讲课教师(如周英)时,必须插入多个(这里是三个)元组:
(物理,周英,普通物理学),(物理,周英,光学原理),(物理,周英,物理习题集) - 删除异常:例如,某一门课(如数学)要去掉一本参考书(如微分方程),则必须删除多个(这里是两个)元组:
(数学,李勇,微分方程),(数学,张平,微分方程)
产生问题的原因在于多值依赖
例如,给定(课程C,教师T),有一组参考书B,这组参考书B仅仅是由课程C决定的,而与教师T无关
- 例如下图中,“李永”和“王军”即便互换也是没有关系的(只要课程是物理)
再比如,给定(课程C,参考书B),有一组教师T,这组教师T仅仅由课程C决定,而与参考书B无关
- 例如下图中,“普通物理学”和“光学原理”即便互换也是没有关系的,教师仍是那些(只要课程是物理)
(2)多值依赖的定义
多值依赖(描述型定义):设$R(U)$是一个属性集$U$上的一个关系模式,$X$、$Y$和$Z$是$U$的子集,并且$Z$=$U$-$X$-$Y$。那么多值依赖$X$->->$Y$成立当且仅当对$R$的任一关系$r$,$r$在($X$,$Z$)上的每个值对应一组$Y$的值,这组值仅仅决定于$X$,而与$Z$无关
- 例如在Teaching(C,T,B)中就有C->->T和C->->B
多值依赖(形式化定义):设$R(U)$是一个属性集$U$上的一个关系模式,$X$、$Y$和$Z$是$U$的子集,并且$Z$=$U$-$X$-$Y$。在$R(U)$的任一关系$r$中,如果存在元组($x$,$y_{1}$,$z_{1}$)和($x$,$y_{2}$,$z_{2}$),则必存在($x$,$y_{2}$,$z_{1}$)和($x$,$y_{1}$,$z_{2}$)。也即交换两个元组的$Y$值所得两个新元组必在$r$中,那么就称$Y$多值依赖于$X$,记作$X$->->$Y$
(3)平凡多值依赖与非平凡多值依赖
若$X$->->$Y$,且$Z$=$\emptyset$,则称$X$->->$Y$为平凡多值依赖
若$X$->->$Y$,且$Z$!=$\emptyset$,则称$X$->->$Y$为非平凡多值依赖
(4)多值依赖的性质
对称性:$Y$多值依赖于$X$,必有$Z$多值依赖于$X$。也即若$X$->->$Y$,$X$->->$Z$,其中$Z$=$U$-$X$-$Y$
函数依赖是多值依赖的特例:若$X$->$Y$,则有$X$->->$Y$
传递性:若$X$->->$Y$,若$Y$->=>$Z$,则若$X$->->$Z-Y$
(5)多值依赖与函数依赖的区别
- 函数依赖规定某些元组不能出现在关系中;多值依赖要求某种形式的其它元组必须在关系中
- 有效性范围不同
(6)多值依赖的解决方法
解决方法仍然是模式分解
二:码
(1)码的相关概念
候选码:若关系中的某一属性组(注意是组不是某单个属性,当然有时属性组也可能只有一个属性)能唯一地标识一个元组,而其子集不能,则该属性组称之为候选码
- 上面关系中,学号是无法区分的,因为学号虽然不重复,但一个学生可能会对应多个课程,这就导致学号无法唯一标识一个元组。因此这里(学号,课程名)可以作为一个候选码
- 需要注意的是候选码不一定只有一个,可能有多个,只要满足条件即可,但在本例中确实只有一个
超码:能够唯一标识一条记录的属性或属性集,超码是候选码的扩充,候选码是最小的超码
- 可以用线性代数理解,就像一个向量组秩为$r$,再填一个能被其线性表示的向量,该向量组秩仍为$r$
- 上面关系中,(学号、课程名)是候选码,那么它的超集,例如(学号、课程名、姓名)、(学号、课程名、性别)就是超码
主码:某个能够唯一标识一条记录的最小属性集(候选码中的“人选之子”)
- 候选码可能有多个,但是数据库设计者在设计时会根据实际需求选择一个候选码作为主码
外码:是本关系的属性且不是码,而是另一个关系的主码(相信再不用我详细介绍了吧)
全码:这是一种特殊情况:关系的所有属性组是这个关系模式的候选码
主属性和非属性:包含在候选码中的属性(注意是集合,不是某个候选码)称为主属性;不包含在候选码中的属性称为非主属性
- 上面关系中,姓名、性别和期末分数都是非主属性
(2)求解候选码
(此部分暂略,后续详细补充)
三:范式
范式:关系数据库中的关系是要满足一定要求的,满足不同程度要求的为不同范式。也即范式是符合某一种级别的关系模式的集合。级别越高,表设计的就越合理
- 第一范式(1NF)
- 第二范式(2NF)
- 第三范式(3NF)
- BC范式(BCNF)
- 第四范式(4NF)
- 第五范式(5NF)
注意:一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式的集合,这种过程就叫规范化
下面的讲解中,以关系模式为例$$SLC(Sno,Sdept,Sloc,Cno,Grade)$$
涉及依赖关系如下
(1)1NF
A:定义
1NF:直观讲,就是关系中任何一列不能再分为两列或更多列
如下关系中,地址这个属性就是可以再分。所以该关系不满足1NF
- 有的人可能只会写某个省某个市
- 有的人可能会写的非常详细
- 所以“地址”这个属性是可以拆分的
- 但是如果写成“省市县”这三列,那么就不能分了,也就满足1NF了
B:1NF可能存在的问题
本例中SLC满足1NF,但却不是一个好的关系模式,因为会存在以下问题
- 插入异常:例如,插入一个学生,其
Sno、Sdept、Sloc属性都具备,但是由于没有选课,所以没有Cno,而Sno和Cno是主码,主码不能为空(否则违背实体完整性),所以无法插入 - 删除异常:例如,某一个学生只选了一门课,假如因为某种原因这门课不选了,那么意味着
Cno和Grade应该删除。但是这会导致整个元组被删除,一些不该删除的信息也被删除了 - 更新异常:例如,某一个学生转了专业,换了系,本来只需修改
Sdept即可,但是Sdept->Sloc,这就导致Sloc也得修改。另外如果这个学生选了k门课,那么这意味着需要重复修改k次,不仅存储冗余度大,而且修改很复杂
C:产生这些问题的原因及解决方法
问题原因:非主属性Sdept、 Sloc部分函数依赖于码

解决方法(2NF的处理方法):进行模式分解,消除部分函数依赖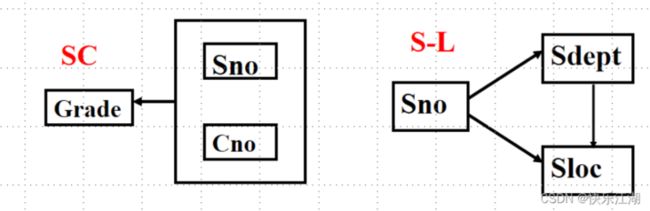
- 关系SC的码为(Sno,Cno)
- 关系Sno的码为(Sno)
(2)2NF
A:定义
2NF:直观讲,就是一个表中只能保存一种数据,不能把多种数据保存在同一张表中。专业定义就是保证每个非主属性对码都是完全函数依赖
其实在1NF的例子中我们可以发现,SLC表似乎有点“不对劲”,就是一张表即在保存成绩又在保存学生的一些基本信息,从语义上讲,这就属于把多种数据保存在了同一张表上。也即是把原本两个关系硬塞在了一起,这就导致(Sno,Cno)在决定Grade的同时,会间接影响到Sdept和Sloc
B:2NF可能存在的问题
在分解后的S-L关系中,它满足2NF但并不是一个好的关系模式。其中Sloc对Sno传递函数依赖,这仍然会导致上面所展示的那些异常情况
(3)3NF
A:定义
3NF:直观讲,就是确保表中的每一列数据都和主码直接相关,而不是间接相关。专业定义就是保证每个非主属性对码既不是部分函数依赖也不是传递函数依赖
在2NF的那个例子中我们可以发现,S-L关系中Sno和Sdept是直接关系,Sdept和Sloc是直接关系,这就导致Sno与Sloc是间接关系。所以我们的做法依旧是采用模式分解,消除传递函数依赖
- 关系S-D的码是
Sno - 关系D-L的码是
Sdept
B:注意
如果一个关系满足3NF,那么可以说在很多情况下它已经合格了。但是在一些特殊情况下,仍然会产生一些异常情况和数据冗余
(4)BCNF
A:定义
BCNF:直观讲,BCNF是修正的第三范式,修正了每一属性对候选码的传递依赖。BCNF一定是3NF,但3NF不一定是BCNF,想要让一个3NF成为BCNF,必须满足
- 所有的非主属性对每一个码都是完全函数依赖
- 所有的主属性对每一个不包含它的码也是完全函数依赖
- 没有任何属性完全函数依赖于非码的任何一组属性
B:判断一个3NF是否是BCNF
方法:
- 找出候选码
- 判断除候选码外是否还有其他决定因素。如果没有那么那么它就是BCNF
如果还有其他决定因素且每个决定因素都包含码那么就是BCNF,否则不是
演示:
【例】有关系模式S(Sno,Sname,Sdept,Sage),其中Sname也具有唯一性
答:这样一来,S就有两个码,且都由单属性组成,彼此不相交,其他属性不存在对码的部分和传递依赖,所以S属于3NF。又因为每一个决定因素中都包含码,所以属于BCNF
【例】关系模式STJ(S, T, J)中,S表示学生,T表示教师,J表示课程。并且
- 每一名教师只教一门课
- 每门课有若干教师
- 某一学生选定某门课,就对应了一个固定的教师
答:于是,有如下依赖
可见(S,J)与(S,T)都是候选码,由于没有任何非主属性对码传递依赖或部分依赖,所以STJ属于3NF。决定因素有(S,J)、(S,T)和T,但T不包含码,所以不属于BCNF
C:3NF和BCNF的关系
- BCNF一定是3NF,但3NF却不一定是BCNF
- 3NF和BCNF是在函数依赖的条件下对模式分解所能达到的分离程度的测度
- 一个模式中的关系模式如果都属于BCNF,那么在函数依赖范畴内它已实现了彻底的分离,已消除了插入和删除的异常
- 3NF的“不彻底”性表现在可能存在主属性对码的部分依赖和传递依赖
(5)4NF(看过多值依赖再看)
4NF:简单点说,要想满足4NF,那么该关系模式的多值依赖要么是平凡的;如果是非平凡的,就必须退化为函数依赖。也就是说非平凡又非函数依赖的多值依赖是不允许存在的
在上面提到的Teaching(C,T,B)显然不是4NF,该关系存在$C$->->$T$和$C$->->$B$两个多值依赖,但是都是非平凡的,所以需要进行模式分解。分解为他们便是平凡的
- $C$->->$T$和$C$->$B$都是平凡多值依赖
四:规范化小结
规范化的基本思想是逐步消除数据依赖中不合适的部分,使模式中的各关系模式达到某种程度的“分离”,即“一事一地”的模式设计原则。让一个关系描述一个概念、一个实体或者实体间的一种联系。若多于一个概念就把它“分离”出去。因此所谓规范化实质上是概念的单一化