脑壳二

多传感器分布式融合算法——多传感器网络协同目标跟踪和定位

多传感器分布式融合算法

应用：

多传感器网络协同目标跟踪及定位

原创不易，路过的各位大佬请点个赞

主要讲解算法：
多传感器集中式融合算法/分布式融合算法/序贯融合算法
多速率多传感器异步融合算法
多传感器网络分布式一致滤波

应用于: 多传感器网络协同跟踪/定位/导航

联系WX: ZB823618313

多传感器分布式融合算法
多传感器网络协同目标跟踪及定位
- 1. 多传感器数据融合系统结构
- - 1.1 集中式融合
  - 1.2 分布式融合
  - 1.3 混合式融合
- 2. 分布式融合结构及对分布式融合理解
- - 2.1 分布式融合结构及深入理解
  - 2.2 航迹融合结构分类
  - - 2.2.1 传感器到传感器的航迹融合
    - 2.2.2 传感器到系统的航迹融合
- 3. 分布式融合困难的原因分析
- - 3.1 航迹融合中各传感器局部估计误差相关
  - - 3.1.1 共同的先验估计
    - 3.1.2 共同的过程噪声
  - 3.2 各传感器量测噪声相关
  - 3.3 局部动态模型不同
  - 3.4 分布式系统的网络结构和信息模式复杂
- 4. 分布式融合算法总结
- - 4.1 简单凸组合SCC融合算法
  - 4.2 Bar-Shalom-Campo融合算法
  - 4.3 协方差交叉CI融合算法
  - 4.4 分布式信息滤波器算法
  - 4.5 带反馈的最优分布式融合算法
  - 4.6 不带反馈的最优分布式融合算法
  - 4.7 最大后验概率MAP融合算法
  - 4.8 最大似然概率ML融合算法
  - 4.9 最大信息熵KL融合算法
  - 4.10 联邦卡尔曼滤波器算法
  - 4.11 基于最优统一融合准则的融合算法
  - - 4.11.1 最优线性无偏估计融合BLUE
    - 4.11.2 加权最小二乘融合WLS
- 5. 基于分布式融合的交互式多模型IMM机动目标跟踪
- - 5.1 算法种类
  - 5.2 参数设置
  - 5.3 实验结果
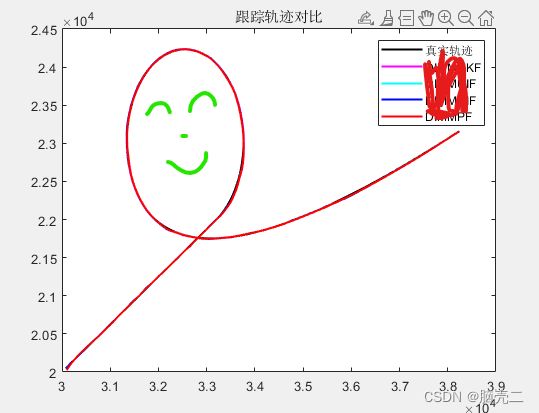
  - - 5.3.1 跟踪轨迹
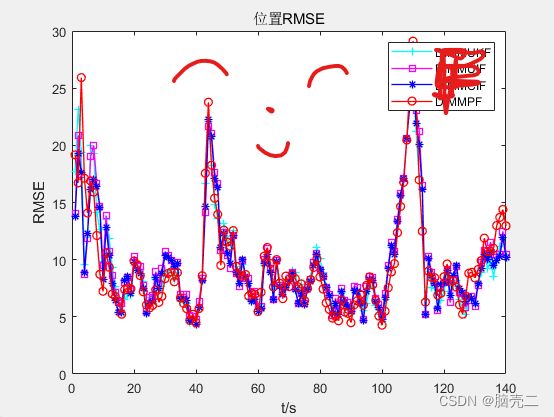
    - 5.3.2 位置均方误差RMSE
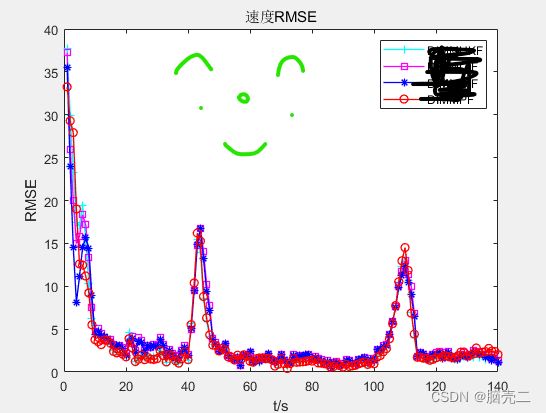
    - 5.3.3 速度均方误差RMSE
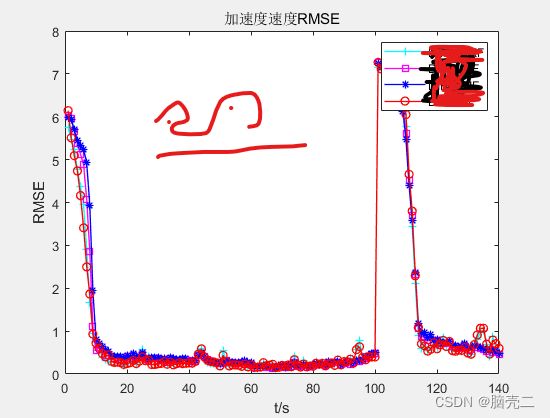
    - 5.3.4 加速度均方误差RMSE
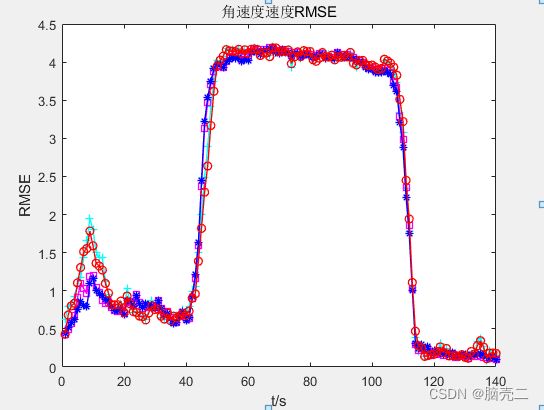
    - 5.3.5 角速度均方误差RMSE
- 6. 代码

1. 多传感器数据融合系统结构

根据系统需求(成本、安全性、可维护性等)以及外界环境(自然环境、人为对抗环境),信息融合系统的结构一般可划分为:集中式结构、分布式结构以及混合式结构,下面以目标跟踪为背景,分别介绍这三种结构。

1.1 集中式融合

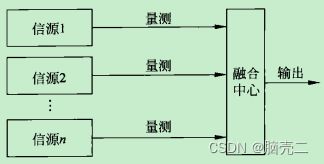
集中式结构的特点是将各个传感器的量测传给融合中心,由融合中心统一进行目标跟踪处理。所以集中式融合也称之为中心式融合或量测融合。该结构充分利用了信源的信息,系统信息损失小,性能比较好,但系统对通信带宽要求较高,系统的可靠性较差。

集中式融合可以得到最优的融合结果。但这种结构需要频带很宽的数据传输链路来传输原始数据,并且需要有较强处理能力的中心处理器,所以工程上实现起来较为困难。

图1：集中式融合

集中式融合一般包含：
1）量测堆叠融合（批处理方式）
2）序贯处理融合
3）数据压缩

1.2 分布式融合

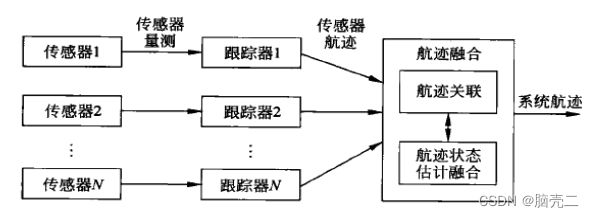
分布式融合(distributed fusion)也称为传感器级融合或自主式融合。在这种结构中,每个传感器都有自己的处理器,进行一些预处理,然后把中间结果送到中心结点,进行融合处理。由于各传感器都具有自己的局部处理器,能够形成局部航迹，所以在融合中心也主要是对各局部航迹进行融合，因此这种融合方法通常也称为航迹融合( track fusion)。这种结构因对信道容量要求低,系统生命力强,工程上易于实现而受到很大重视v并成为信息融合研究的重点。分布式航迹融合系统根据其通信方式的不同又可分为:

1）无反馈分层融合结构：各传感器结点把各自的局部估计全部传送到中心结点以形成全局估计,这是最常见的分布式融合结构。

图2：无反馈分层融合结构 \\

2）有反馈分层融合结构：在这种结构中,中心结点的全局估计可以反馈到各局部结点,它具有容错的优点。当检测出某个局部结点的估计结果很差时,不必把它排斥于系统之外,而是可以利用全局结果来修改局部结点的状态。这样既改善了局部结点的信息,又可继续利用该结点的信息。文献5证明了此种结构并不能改善融合系统的性能,但可以提高局部估计的精度。

图3：有反馈分层融合结构 \\

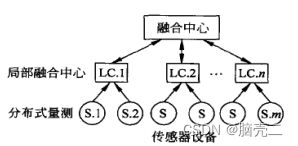
分布式结构的特点是先由各个信源模块对所获取的量测进行跟踪处理,然后再对各个传感器形成的目标航迹进行融合。该结构的信息损失大于集中式结构,性能较集中式略差,但可靠性高,并且对系统通信带宽要求不高。

从不同的角度，分布式融合也可以分为不同类型。分布式结构也可以分为三种形式:
1）有融合中心的分布式结构
2）无融合中心,共享航迹的分布式结构
3）无融合中心,共享关联量测的分布式结构。`

笔记：

多传感器分布式融合也是估计融合领域最热门的邻域之一，也是目前两大学者在融合邻域关注的焦点

此外，分布式融合算法种类非常多，研究角度也各不相同。换句话说，分布式融合本身就是一个非常大的方向

分布式融合也是本博客主要介绍的融合方式之一。本博客主要介绍分布式融合中最常用、最普遍的一种算法。

1.3 混合式融合

混合式结构是集中式和分布式两种结构的组合,同时传送各个信源的量测以及各个信源经过跟踪处理的航迹,综合融合量测以及目标航迹。该结构保留了集中式和分布式两种结构的优点,但在通信带宽、计算量、存储量上一般要付出更大的代价。

2. 分布式融合结构及对分布式融合理解

·按理说，应该先写集中式融合的博客。但是，不重要。哈哈哈哈哈哈哈

先上分布式融合两个定义。当然，我也不知道这两个定义对大家有没有用。反正定义是抄的。

定义1 在多传感器融合系统中,每个传感器的跟踪器所给出的航迹称作局部航迹(local track)或传感器航迹(sensor track)。

定义2 航迹融合系统将各个局部航迹或传感器航迹融合后形成的航迹称作系统航迹(system track)或全局航迹(global track)。当然,将局部航迹或传感器航迹与系统航迹融合后形成的航迹仍然称为系统航迹。

2.1 分布式融合结构及深入理解

分布式融合结构中研究最广泛，关注度最高、挑战最大的就是航迹融合。所谓航迹融合，就是各个传感器向融合中心或者别的传感器传送目标的“航迹”，而不是传感器本身直接观测得到的数据。

这里有个提醒的是，很多人把分布式融合与航迹融合等价。实际上，分布式融合包含了航迹融合。航迹融合只是分布式融合的一个子集。只是航迹融合应用最广泛而已

还有一种分布式融合，各个局部传感器向融合中心或者其它传感器传输的不是“航迹”，也不是“原始量测”，而是一种处理过的量测。多为处理过的量测，表现形式有很多种型式，一般可以称它们为伪量测。这种分布式融合的论文其实也很多，研究前景也很大。

还还还有一种分布式融合，哈哈哈哈哈，其实。该种分布式融合是那种呢？它们是集中式融合的变体。因此有着一般有着最优的融合性能。
比较典型的有：

有反馈分布式融合；

无反馈分布式融合；

联邦卡尔曼滤波

信息滤波器。
不过这种分布式融合，有学者认为，它们是集中式融合往航迹融合的变体，目的地还是航迹融合

本博客还是主要介绍分布式融合中的航迹融合。

航迹融合包含两步:航迹关联和航迹状态估计融合。在航迹关联过程中,来自不同传感器的航迹进行关联以形成系统航迹,每个传感器的航迹相应于一个单独的假定的目标。给定了一个关联过程之后,系统航迹的状态估计就可以通过融合关联上的传感器航迹的状态估计来得到。

根据是否利用系统航迹的状态估计,航迹融合通常有两种可能的处理结构。

图4：航迹融合系统结构 \\

2.2 航迹融合结构分类

2.2.1 传感器到传感器的航迹融合

传感器到传感器的航迹融合结构如图6-3-2所示,可以看出,来自不同传感器航迹(传播到同一时刻)的状态估计互相之间进行关联和融合以得到系统航迹的状态估计。在这一过程中不利用系统航迹以前的状态估计。要注意的是,对于这种结构,融合一般来说包含来自多于两个传感器的航迹集合。

图5：传感器到传感器的航迹融合 \\

这种结构不必处理相关估计误差的问题(如果忽略掉共同的先验信息)。由于它基本上是一个无记忆的操作,所以关联和航迹估计融合中的误差不会从一个时刻传播到下一时刻。然而,由于过去的处理结果被丢弃掉了,这一方法可能没有传感器到系统的融合结构有效。

2.2.2 传感器到系统的航迹融合

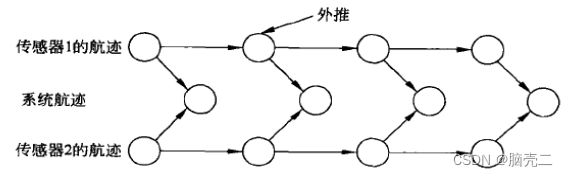
无论什么时候接收到一组传感器航迹﹐系统航迹的状态估计被外推到传感器航迹的时刻,并且与最新接收到的传感器航迹进行融合。当接收到另外一组传感器航迹时,重复这一过程。

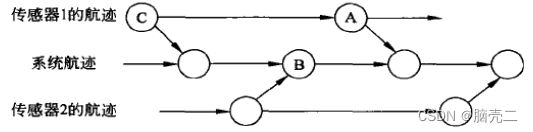
传感器到系统的航迹融合把关联问题简化成-一个bi-partite分配问题,所以可以利用常见的分配算法。然而,它必须处理相关估计误差的问题。在图6-3-3中,A点的传感器航迹和B点的系统航迹具有相关的误差,原因是它们都依赖于C点。进一步说,由于关联或融合中过去处理误差导致的系统航迹中的任何误差会影响将来的融合性能。

center>图6：传感器到系统的航迹融合 \

3. 分布式融合困难的原因分析

3.1 航迹融合中各传感器局部估计误差相关

如果各传感器局部估计误差之间互不相关,相应的融合算法非常简单。

但在一般情况下,这一假设是不满足的,即各传感器的局部估计误差之间是相关的,具体原因如下所述。

3.1.1 共同的先验估计

这种情况发生在传感器到系统的航迹融合结构中

要么是一个量测和一条航迹的融合,要么是一条航迹和另外一条航迹的融合。假定航迹已经被传播到一个共同的时刻。基本上来说,在一个结点的一条航迹会包含祖先结点（航迹和量测）中的所有信息。传感器航迹估计和系统航迹估计，都包含从较早时刻传播来的传感器航迹估计。因此，即使两条传感器航迹不共享共同的先验估计(除共同的先验)，但是随着递推传播，传感器的航迹和系统航迹由于共同的先验信息，必然存在相关。一般来说,如果在信息图中从量测到融合结点存在多径，也存在这一信息源引起的相关。

3.1.2 共同的过程噪声

这种情况甚至发生在传感器航迹不共享共同的量测而进行融合时

当目标动态方程不确定时,给定某一时刻的目标状态,来自两条传感器航迹的量测不一定条件独立。这样一来,来自两条传感器航迹的估计误差就可能不独立。

假定有两条航迹 $i$ 和 $j$ 状态估计(估计或预测)和相应的误差协方差矩阵(都传播到同一时刻)分别为： $\hat{x}_i$ 和 $\hat{x}_j$ ， ${P}_i$ 和 ${P}_j$ 。估计融合问题就是找到最好的融合估计i和误差协方差矩阵 ${P}$ 。这两条航迹可能是一个传感器到传感器航迹融合结构中的两条航迹,或者是一个传感器到系统航迹融合结构中的一条系统航迹和一条传感器航迹。

还有两个导致航迹融合中各传感器局部估计误差相关的原因分别为：
各局部传感器观测误差相关
各局部航。迹采用的目标动力学建模是一样的
这两个原因在下面单独分析，因为它们还会导致的困难不仅仅是使局部估计误差相关

3.2 各传感器量测噪声相关

基于卡尔曼滤波的集中式/分布式融合框架要求，不同来源的观测误差必须是不相关的。在许多实际情况下，这是一个真正的限制。例如，许多传感器误差依赖于常见的随机估计对象(即待估计的数量)，因此是相关的。另一个例子是，在一个共同的噪声环境中，被估计对象被多个传感器观测到，例如在由目标产生的噪声干扰期间。

传感器噪声相关，直接导致局部航迹相关。

3.3 局部动态模型不同

实际上，现在基本上所有的跟踪融合论文，都默认局部估计的动力学模型和融合中心的动力模型一致。也就是说，融合中，过程烟花模型只是一个。这显然不能符合分布式的思想。分布式各局部估计中心，一般应该拥有自己的建模。

基于卡尔曼滤波的集中式融合框架要求，局部动态模型必须相同。在现实中，局部估计可能是基于被评估者的不同动态模型来获得的，以考虑来源特定的情况或需求。对局部估计器使用不同的动态模型可能是必要的或更有效的。这是必要的，例如，当状态增强用于一些具有自相关传感器观测噪声的局部估计。例如，当一个局部估计器中使用多个模型时，它可能更有效。为了获得最好的融合性能，局部模型的选择当然不是随意的。

3.4 分布式系统的网络结构和信息模式复杂

基于卡尔曼滤波的集中式/分布式融合框架要求，分布式系统的网络结构和信息模式必须简单。这种局限性显然源于这样一个事实:当分布式系统过于复杂时，实际上不可能通过使用局部估计重构集中式融合规则来设计融合规则。

4. 分布式融合算法总结

下面只是简单罗列比较经典且常用的分布式融合算法。针对这些算法的细节及实验，在后续的博客中具体讲解，

如果等不急，可以直接联系博主。

4.1 简单凸组合SCC融合算法

4.2 Bar-Shalom-Campo融合算法

4.3 协方差交叉CI融合算法

4.4 分布式信息滤波器算法

4.5 带反馈的最优分布式融合算法

4.6 不带反馈的最优分布式融合算法

4.7 最大后验概率MAP融合算法

4.8 最大似然概率ML融合算法

4.9 最大信息熵KL融合算法

4.10 联邦卡尔曼滤波器算法

4.11 基于最优统一融合准则的融合算法

4.11.1 最优线性无偏估计融合BLUE

4.11.2 加权最小二乘融合WLS

备注：如果大家还了解其它的比较常用的分布式融合算法，可以在评论区留言。
** 大家如果还有其它想了解的融合算法，可以在评论区说出来。 **

5. 基于分布式融合的交互式多模型IMM机动目标跟踪

讲了这么多，还不如直接弄一个实例。

既然是第一篇关于分布式融合的博客，实例直接上比较复杂的。哈哈哈哈哈哈

5.1 算法种类

算法：基于简单凸组合SCC的交互式多模型无迹卡尔曼滤波
  基于协方差交叉CI的交互式多模型无迹卡尔曼滤波
  交互式多模型分布式无迹信息滤波融合
  基于协方差交叉CI的交互式多模型粒子滤波

5.2 参数设置

运动模型： 近匀速CV模型 $\dot{x}, \dot{y}]^T$
$X_{k+1}=\begin{bmatrix}1&0&T&0\\0&1&0&T\\0&0&1&0\\0&0&0&1 \end{bmatrix}X_{k} + W_k$
其中 $W_k$ 为零均值白噪声，其方差为：
$Q_k=q_k^2\begin{bmatrix}T^3/3&T^2/2&0&0 \\T^2/2&T&0&0 \\0&0&T^3/3&T^2/2 \\0&0& T^2/2&T\end{bmatrix}$

仅匀转弯CT模型 $\dot{x}, \dot{y}, w]^T$
$X_{k+1}=\begin{bmatrix}1&\frac{\sin(\omega T)}{\omega}&0&-\frac{1-\cos(\omega T)}{\omega}&0\\0&\cos(\omega T)&0&-\sin(\omega T)&0\\0&\frac{1-\cos(\omega T)}{\omega}&1&\frac{\sin(\omega T)}{\omega}&0\\0&\sin(\omega T)&0&\cos(\omega T)&0\\0&0&0&0&1\end{bmatrix}X_{k} + W_k$
其中 $W_k$ 为零均值白噪声，其方差为：
$Q_k=q_k^2\begin{bmatrix}T^3/3&T^2/2&0&0& 0 \\T^2/2&T&0&0 &0\\0&0&T^3/3&T^2/2 &0 \\0&0& T^2/2&T&0\\0&0&0&0&q_w\end{bmatrix}$
或者为(两种形式都可以用，下面一代码形式给出)
近匀加速CA模型 $\dot{x},\dot{y},\ddot{x}, \ddot{y}]^T$
$X_{k+1}=\begin{bmatrix}1&0&T&0&T^2/2&0\\0&1&0&T&0&T^2/2\\0&0&1&0&T&0 \\0&0&0&1&0&T \\0&0&0&0&1&0 \\0&0&0&0&0&1 \end{bmatrix}X_{k} + W_k$
其中 $W_k$ 为零均值白噪声，其方差为：

Qk3=q3^2*[T^5/20   0      T^4/8  0       T^3/6   0;
          0       T^5/20  0      T^4/8   0       T^3/6;
          T^4/8   0       T^3/3  0       T^2/2   0;
          0       T^4/8   0      T^3/3   0       T^2/2;
          T^3/6   0       T^2/2  0       T       0
          0       T^3/6   0      T^2/2   0       T];

传感器： 多个主动雷达
在二维情况下，雷达量测为距离和角度
${r}_k^m=r_k+\tilde{r}_k\\ b^m_k=b_k+\tilde{b}_k$
其中
$r_k=\sqrt{(x_k-x_0)^+(y_k-y_0)^2)}\\ b_k=\tan^{-1}{\frac{y_k-y_0}{x_k-x_0}}\\$
$x_0,y_0]$ 为雷达坐标，一般情况为0。雷达量测为 $z_k=[r_k,b_k]'$ 。雷达量测方差为
$R_k=\text{cov}(v_k)=\begin{bmatrix}\sigma_r^2 & 0 \\0 & \sigma_b^2 \end{bmatrix}$

5.3 实验结果

5.3.1 跟踪轨迹

5.3.2 位置均方误差RMSE

5.3.3 速度均方误差RMSE

5.3.4 加速度均方误差RMSE

5.3.5 角速度均方误差RMSE

6. 代码

代码仅为部分代码，也是一个案例。
如果需要分布式融合算法代码，和论文复现，WX：ZB823618313


close all;
clear all;
clc;
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%系统参数设置
runs=5; %蒙特卡洛实验次数，滤波将进行50次
steps=140; %跟踪总时长
M=5;% 雷达数量
nz=2;% 测量维数
T=1;% 采样时间
%模型1：CV模型x=[x位置， y位置， x速度， y速度]'：的动态方程参数设置,Xk+1=fk(Xk)+G*uk+Gk*Wk,CV模型
Fk_cv=[1 0 T 0;
       0 1 0 T;
       0 0 1 0;
       0 0 0 1];% 
q1=0.01; % 目标运动学标准差，过程噪声
% % Qk1=q1*[T^3/3, 0,     T^2/2,   0;
% %           0      T^3/3, 0        T^2/2;
% %           T^2/2, 0      T^2        0
% %           0      T^2/2  0        T^2];% 过程噪声协方差
% % Gk_cv= eye(4); %过程噪声增益矩阵
Gk_cv= [ T^2/2  0
       0     T^2/2      
       T       0
       0      T]; %过程噪声增益矩阵
Qk1=q1^2*eye(2);
%模型2：CT模型x=[x位置， y位置， x速度， y速度， 角速度]' 的动态方程参数设置,Xk+1=fk(Xk)+G*uk+Gk*Wk,CT模型
Fk_ct=@(w1)[1           0      sin(w1*T)/w1      -(1-cos(w1*T))/w1   0;
       0         1      (1-cos(w1*T))/w1   sin(w1*T)/w1       0;
       0         0      cos(w1*T)         -sin(w1*T)          0;
       0         0      sin(w1*T)          cos(w1*T)          0
       0         0      0                  0                  1;];% CT模型的系统矩阵是关于状态x(5)的函数，即转弯角速度w的函数
q2 = 0.01;
q_ctw=1.75e-8;% CT模型角速度过程噪声方差
% 角速度定常数


randn('state',sum(100*clock));  %每次给不同的状态重置随机数产生器（因为clock每次都不同）

%%

for index=1:runs %蒙特卡洛次数
    index         %显示运行次数
    %滤波初始化设置
    % CV
    X_cv=[30000,20000,80,50]';
    P_cv=diag([1e5,1e5,1e3,1e3]);
    % CT
    w1 = 4.5*pi/180;% 初始角速度
    w2 = -6*pi/180;% 初始角速度
    X_ct=[30000,20000,80,50 w1]';
    P_ct=diag([1e5,1e5,1e3,1e3,1e-6]);
    % CA
    acc=[6;5];
    X_ca=[30000,20000,80,50, acc']';
    P_ca=diag([1e5,1e5,1e3,1e3,1e-2,1e-2]);
    %滤波初始化
    X_cv_zero=X_cv+sqrtm(P_cv)*randn(4,1);%产生真实X0
    X_ct_zero=X_ct+sqrtm(P_ct)*randn(5,1);%产生真实X0
    X_ca_zero=X_ca+sqrtm(P_ca)*randn(6,1);%产生真实X0
%IMMUKF三个滤波器的初始化   
    xk_UKFcv=X_cv_zero;             %X(0|0)= X_aver_zero
    Pk_UKFcv=P_cv;                  %P(0|0)= P_zero
    xk_UKFct=X_ct_zero;
    Pk_UKFct=P_ct;
    xk_UKFca=X_ca_zero;
    Pk_UKFca=P_ca;
    for m=1:M
        xk_UKF{m}={xk_UKFcv, xk_UKFct, xk_UKFca};
        Pk_UKF{m}={Pk_UKFcv, Pk_UKFct, Pk_UKFca};