《Python数据分析与挖掘实战》第10章(上)——DNN1 背景与目标分析2 数据探索3 数据预处理
本文是基于《Python数据分析与挖掘实战》的实战部分的第10章的数据——《家用电器用户行为分析与事件识别》 做的分析。
旨在补充原文中的细节代码,并给出文中涉及到的内容的完整代码;另外,原文中的数据处理部分排版先后顺序个人感觉较为凌乱,在此给出梳理。
在作者所给代码的基础上增加的内容包括:
1)在数据规约部分: 书中提到:规约掉热水器"开关机状态"=="关"且”水流量”==0的数据,说明热水器不处于工作状态,数据记录可以规约掉。但由后文知,此条件不能进行规约 因为,"开关机状态"=="关"且”水流量”==0可能是一次用水中的停顿部分,删掉后则无法准确计算关于停顿的数据
2)在一次完整用水事件的划分模型中: 将时间间隔列数据离散并面元,探索了不同时间间隔中,用水事件的个数; 画用水停顿时间间隔频率分布直方图; 确定一次用水事件停顿阈值,然后划分一次完整用水事件。
3)用水事件阈值寻优模型: 通过频率分布直方图-确定阈值的变化与划分得到的事件个数关系 通过图像中斜率指标-确定阈值的变化与划分得到的事件个数关系
4)属性构造中: 原书中只给出了需要构造的属性的定义,并未给出具体代码,本文给出了具体的代码;并给出了两种方法求用水事件的时间间隔
5)模型构造: 添加了显示混淆矩阵可视化预测结果,查看训练结果正确率
1 背景与目标分析
根据热水器厂商提供的数据进行分析,对用户的用水事件进行分析,判断用水是否是洗浴事件, 识别不同用户的用水习惯,以提供个性化的服务。
实质:二分类问题
2 数据探索
首先,通过频率分布直方图分析用户用水停顿时间间隔的规律性;然后,探究划分一次完整用水事件的时间间隔阈值。
data = pd.read_excel('original_data.xls',encoding='gbk')
[/code]
```code
data[u'发生时间'] = pd.to_datetime(data[u'发生时间'], format = '%Y%m%d%H%M%S')#将该特征转成日期时间格式(***)
data = data[data[u'水流量'] > 0] # 只要流量大于0的记录
# print len(data) #7679
data[u'用水停顿时间间隔']= data[u'发生时间'].diff()/ np.timedelta64(1, 'm') #将datetime64[ns]转成 以分钟为单位(*****)
data= data.fillna(0) # 替换掉data[u'用水停顿时间间隔']的第一个空值
[/code]
## 2.1 数据质量分析
```code
#-----第*1*步-----数据探索,查看各数值列的最大最小和空值情况
data_explore = data.describe().T
data_explore['null'] = len(data)-data_explore['count']
explore = data_explore[['min','max','null']]
explore.columns = [u'最小值',u'最大值',u'空值数']
explore
[/code]

## 2.2 数据特征分析
### 2.2.1 分布分析
```code
#----第*2*步-----离散化与面元划分
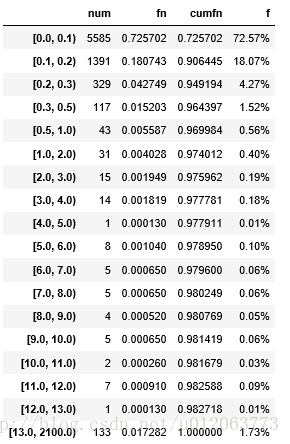
# 将时间间隔列数据划分为0~0.1,0.1~0.2,0.2~0.3....13以上,由数据描述可知,
# data[u'用水停顿时间间隔']的最大值约为2094,因此取上限2100
Ti = list(data[u'用水停顿时间间隔'])#将要面元化的数据转成一维的列表
timegaplist = [0.0,0.1,0.2,0.3,0.5,1,2,3,4,5,6,7,8,9,10,11,12,13,2100]# 确定划分区间
cats = pd.cut(Ti,timegaplist,right=False) # 包扩区间左端,类似"[0,0.1)",(默认为包含区间右端)
x = pd.value_counts(cats)
x.sort_index(inplace = True)
dx = DataFrame(x,columns=['num'])
dx['fn'] = dx['num']/sum(dx['num'])
dx['cumfn'] = dx['num'].cumsum()/sum(dx['num'])
f1 = lambda x :'%.2f%%' % (x*100)
dx[['f']]= dx[['fn']].applymap(f1)
dx
[/code]
```code
#-----第*3*步-----画用水停顿时间间隔频率分布直方图
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
dx['fn'].plot(kind='bar')
plt.ylabel(u'频率/组距')
plt.xlabel(u'时间间隔(分钟)')
p = 1.0*dx['fn'].cumsum()/dx['fn'].sum()# 数值等于 dx['cumfn'],但类型是列表
dx['cumfn'].plot(color = 'r', secondary_y = True, style = '-o',linewidth = 2)
plt.annotate(format((p[4]), '.4%'), xy = (7, p[4]), xytext=(7*0.9, p[4]*0.95), arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) #添加注释,即85%处的标记。这里包括了指定箭头样式。
plt.ylabel(u'累计频率')
plt.title(u'用水停顿时间间隔频率分布直方图')
plt.grid(axis='y',linestyle='--')
# fig.autofmt_xdate() #自动根据标签长度进行旋转
for label in ax.xaxis.get_ticklabels(): #此语句完成功能同上,但是可以自定义旋转角度
label.set_rotation(60)
plt.savefig('Water-pause-times.jpg')
plt.show()
[/code]
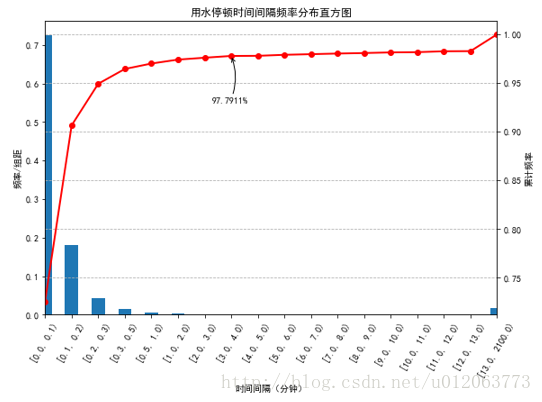
# 3 数据预处理
## 3.1 数据规约
# 规约掉"热水器编号"、"有无水流"、"节能模式"三个属性
# 注意:
#书中提到:规约掉热水器"开关机状态"=="关"且”水流量”==0的数据,说明热水器不处于工作状态,数据记录可以规约掉。但由后文知,此条件不能进行规约
# 因为,"开关机状态"=="关"且”水流量”==0可能是一次用水中的停顿部分,删掉后则无法准确计算关于停顿的数据
```code
or_data = pd.read_excel('original_data.xls',encoding='gbk')
or_data.head()
[/code]

```code
data = or_data.drop(or_data.columns[[0,5,9]],axis=1) # 删掉不相关属性
[/code]
```code
data.to_excel('data_guiyue.xlsx')
data.head()
[/code]

## 3.2 数据变换
### 3.2.1 用水事件阈值寻优模型
根据数据探索部分,初步可以推测,用水事件停顿阈值为四分钟较为合适。但是为了进一步确定是否为四分钟,为此接下来探索的是——用水事件阈值寻优模型。
```code
#第一步:确定阈值与事件数的关系
#****************************
#@1 目标:确定阈值的变化与划分得到的事件个数关系
# 方法:通过频率分布直方图
#****************************
timedeltalist = np.arange(2.25,8.25,0.25)
# 从2.25到8.25间,以间隔为0.25,确定阈值即,阈值范围为[2.25,2.5,2.75,3,...,7.75,8]
counts = [] # 记录不同阈值下的事件个数
for i in range(len(timedeltalist)):
threshold = pd.Timedelta(minutes = timedeltalist[i])#阈值为四分钟
d = data[u'发生时间'].diff() > threshold # # 相邻时间做差分,比较是否大于阈值
data[u'事件编号'] = d.cumsum() + 1 # 通过累积求和的方式为事件编号
temp = data[u'事件编号'].max()
counts.append(temp)
coun = pd.Series(counts, index=timedeltalist)
# 画频率分布直方图
#将阈值与对应的事件数绘制成频率分布直方图,以确定最优阈值
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']= False
plt.rc('figure', figsize=(8,6))
np.set_printoptions(precision=4)
fig = plt.figure()
fig.set(alpha=0.2)#设置图标透明度
ax = fig.add_subplot(1,1,1)
# coun.plot(linestyle='-.',color='r',marker='<')
coun.plot(style='-.r*')#同上
ax.locator_params('x',nbins = int(len(coun)/2)+1) # (****)
ax.set_xlabel(u'用水事件间隔阈值(分钟)')
ax.set_ylabel(u'事件数(个)')
ax.grid(axis='y',linestyle='--') # (****)
plt.savefig('threshold_numofCase.jpg')
plt.show()
由上图可知,图像趋势平缓说明用户的停顿习惯趋于稳定,所以取该段时间开始作为阈值,既不会将短的用水时间合并,也不会将长的用水时间拆开,因此,最后选取一次用水时间间隔阈值为4分钟
利用阈值的斜率指标来作为某点的斜率指标
# 第二步:阈值优化
#****************************
#@2 目标:确定阈值的变化与划分得到的事件个数关系
# 方法:通过图像中斜率指标
#****************************
# 当存在阈值的斜率指标 k ts # 相邻时间做差分,比较是否大于阈值(*****)
return d.sum()+1 # 直接返回事件数(*****)
dt = [pd.Timedelta(minutes = i) for i in np.arange(1,9,0.25)]#(***)
h = DataFrame(dt,columns = [u'阈值']) # 定义阈值列(**)
h[u'事件数'] = h[u'阈值'].apply(event_num) # 计算每个阈值对应的事件数(*****)
h[u'斜率'] = h[u'事件数'].diff()/0.25 # 计算每个相邻点对应的斜率(****)
h[u'斜率指标偏移前'] = pd.rolling_mean(h[u'斜率'].abs(), n)# 采用当前指标和后n个指标斜率的绝对值的平均作为当前指标的斜率
h[u'斜率指标'] = np.nan
h[u'斜率指标'][:-4] = h[u'斜率指标偏移前'][4:]
mink = h[u'斜率指标'][h[u'斜率指标'] < KS]# 斜率指标小于1的值的集合
mink1 = h[u'斜率指标'][h[u'斜率指标'] < KS2]# 斜率指标小于5的值的集合
if list(mink): # 斜率指标值小于1不为空时,即,存在斜率指标值小于1时
minky = [h[u'阈值'][i] for i in mink.index]# 取“阈值最小”的点A所对应的间隔时间作为ts
ts = min(minky) #取最小时间为ts
elif list(mink1):# 当不存在斜率指标值小于1时,找所有阈值中“斜率指标最小”的阈值
t1 = h[u'阈值'][h[u'斜率指标'].idxmin()] #“斜率指标最小”的阈值t1
# ts = h[u'阈值'][h[u'斜率指标偏移前'].idxmin() - n] #等价于前一行作用(*****)
# 备注:用idxmin返回最小值的Index,由于rolling_mean自动计算的是前n个斜率的绝对值的平均,所以结果要平移-n,得到偏移后的各个值的斜率指标,注意:最后四个值没有斜率指标因为找不出在它以后的四个更长的值
if h[u'斜率指标'].min()<5:
ts = t1#当该阈值的斜率指标小于5,则取该阈值作为用水事件划分的阈值
else:
ts = pd.Timedelta(minutes = 4)# 当该阈值的斜率指标不小于5,则阈值取默认值——4分钟
tm = ts/np.timedelta64(1, 'm')
print "当前时间最优时间间隔为%s分钟" % tm
[/code]
至此,确定了一次用水停顿阈值为4分钟,开始划分一次完整事件。
```code
threshold = pd.Timedelta(minutes=4)#阈值为四分钟
d = data[u'发生时间'].diff() > threshold # 相邻时间做差分,比较是否大于阈值(*****)
data[u'事件编号'] = d.cumsum() + 1 # 通过累积求和的方式为事件编号(*****)
data.to_excel('dataExchange_divideEvent.xlsx')
[/code]
### 3.2.3 属性构造
由于属性构造内容较多,因此,本小节单独放在下一篇博客中进行分享。
备注:本章节完整代码详见 [ 点击打开链接
](https://github.com/clover95/DataAnalysisbyPython/tree/master/chapter10)
