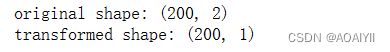机器学习：基于主成分分析（PCA）对数据降维

机器学习：基于主成分分析（PCA）对数据降维

作者：AOAIYI

作者简介：Python领域新星作者、多项比赛获奖者：AOAIYI首页

如果觉得文章不错或能帮助到你学习，可以点赞收藏评论+关注哦！

如果有小伙伴需要数据集和学习交流，文章下方有交流学习区！一起学习进步！

---

专栏案例：机器学习
机器学习：基于逻辑回归对某银行客户违约预测分析
机器学习：学习k-近邻（KNN）模型建立、使用和评价
机器学习：基于支持向量机（SVM）进行人脸识别预测
决策树算法分析天气、周末和促销活动对销量的影响
机器学习：线性回归分析女性身高与体重之间的关系

---

---

一、实验目的

1、了解数据降维的各种算法原理

2、熟练掌握sklearn.decomposition中降维方法的使用

二、实验原理

主成分分析算法（Principal Component Analysis， PCA）的目的是找到能用较少信息描述数据集的特征组合。它意在发现彼此之间没有相关性、能够描述数据集的特征，确切说这些特征的方差跟整体方差没有多大差距，这样的特征也被称为主成分。这也就意味着，借助这种方法，就能通过更少的特征捕获到数据集的大部分信息。

主成分分析原理
设法将原来变量重新组合成一组新的相互无关的几个综合变量，同时根据实际需要从中可以取出几个较少的总和变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，也是数学上处理降维的一种方法。主成分分析是设法将原来众多具有一定相关性（比如P个指标），重新组合成一组新的互相无关的综合指标来代替原来的指标。通常数学上的处理就是将原来P个指标作线性组合，作为新的综合指标。最经典的做法就是用F1（选取的第一个线性组合，即第一个综合指标）的方差来表达，即Va（rF1）越大，表示F1包含的信息越多。因此在所有的线性组合中选取的F1应该是方差最大的，故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息，再考虑选取F2即选第二个线性组合，为了有效地反映原来信息，F1已有的信息就不需要再出现在F2中，用数学语言表达就是要求Cov（F1,F2）=0，则称F2为第二主成分，依此类推可以构造出第三、第四，……，第P个主成分。

sklearn中主成分分析的模型

class sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver=’auto’, tol=0.0, iterated_power=’auto’, random_state=None）

sklearn.decomposition.PCA参数介绍

接下来我们主要基于sklearn.decomposition.PCA类来讲解如何使用scikit-learn进行PCA降维。PCA类基本不需要调参，一般来说，我们只需要指定要降维到的维度，或者希望降维后主成分的方差和占原始维度所有特征方差和的比例阈值就可以了。

现在我们介绍一下sklearn.decomposition.PCA的主要参数：

• 1. n_components：这个参数指定了希望PCA降维后的特征维度数目。最常用的做法是直接指定降维到的维度数目，此时n_components是一个大于等于1的整数。当然，我们也可以指定主成分的方差和所占的最小比例阈值，让PCA类自己去根据样本特征方差来决定降维到的维度数，此时n_components是一个(0,1]之间的浮点数。当然，我们还可以将参数设置为"mle"，此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维。我们也可以使用默认值，即不输入n_components，此时n_components=min(样本数，特征数)。
• 2. whiten：判断是否进行白化。所谓白化，就是对降维后的数据的每个特征进行归一化，让方差都为1。对于PCA降维本身来说，一般不需要白化。如果在PCA降维后有后续的数据处理动作，可以考虑白化。默认值是False，即不进行白化。
• 3. svd_solver：即指定奇异值分解SVD的方法，由于特征分解是奇异值分解SVD的一个特例，一般的PCA库都是基于SVD实现的。有4个可以选择的值：{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。'randomized’一般适用于数据量大，数据维度多同时主成分数目比例又较低的PCA降维，它使用了一些加快SVD的随机算法。'full’则是传统意义上的SVD，使用了scipy库中的实现。‘arpack’和’randomized’的适用场景类似，区别是’randomized’使用的是scikit-learn中的SVD实现，而’arpack’直接使用了scipy库的sparse SVD实现。默认是’auto’，即PCA类会自己去权衡前面讲到的三种算法，选择一个合适的SVD算法来降维。一般来说，使用默认值就够了。

除了这些输入参数外，有两个PCA类的成员值得关注。第一个是explained_variance_，它代表降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分。第二个是explained_variance_ratio_，它代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分。

三、实验环境

Python 3.9

Anaconda 4

Jupyter Notebook

四、实验内容

本实验介绍了主成分分析算法PCA并以实例验证

五、实验步骤

1.数据准备

1.导入所需的模块

import numpy as np  
import matplotlib.pyplot as plt  
import seaborn as sns;sns.set()
%matplotlib inline  

2.构建示例数据

#创建随机数生成器  
rng=np.random.RandomState(1)  
X=np.dot(rng.rand(2,2),rng.randn(2,200)).T  
  
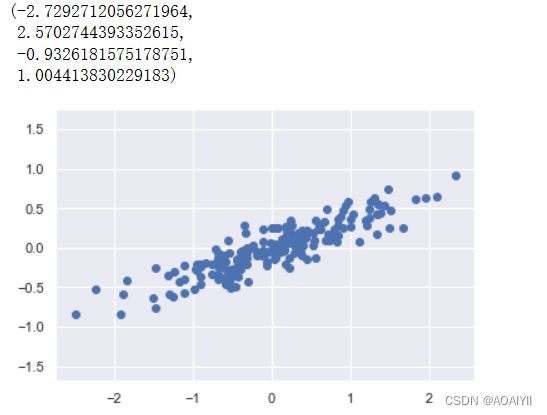
plt.scatter(X[:,0],X[:,1])  
plt.axis("equal") 

如上所示，第一组示例数据为一组样本量为200的随机的二维数组

2.PCA分析

1.导入 Scikit-Learn 中用于主成分分析的 PCA 模块，构建一个主成分分析模型对象，并进行训练。在这次构建中，我们设定 PCA 函数的参数 n_components 为2，这意味这我们将得到特征值最大的两个特征向量

from sklearn.decomposition import PCA  
pca=PCA(n_components=2)  
#使用fit()方法拟合模型  
pca.fit(X)  

n_components参数表示PCA算法中所要保留的主成分个数n，也即保留下来的特征个数n

2.模型训练完成后， components_ 属性可以查看主成分分解的特征向量：

print(pca.components_) 

3.使用.shape方法查看矩阵形状

pca.components_.shape  

4.使用type()方法查看pca.components_类型

type(pca.components_)  

3.查看主成分的解释能力

1.explained_variance_代表降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分

pca.explained_variance_  

4.主成分轴（Principal Axes）的可视化

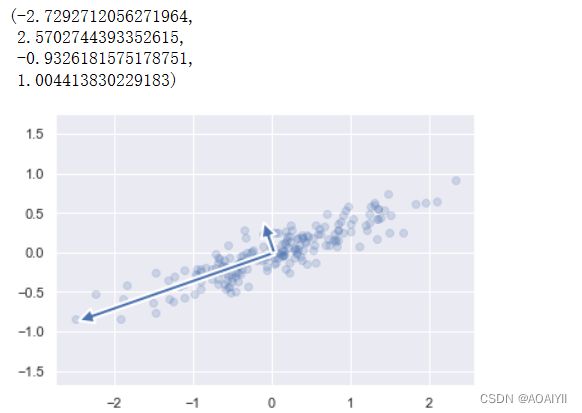
1.我们可以通过如下方式将主成分分析中的特征向量描绘出来，下图中向量的起点为样本数据的均值

def draw_vector(v0,v1,ax=None):  
    ax = ax or plt.gca()  
    arrowprops=dict(linewidth=2,shrinkA=0,shrinkB=0)  
    ax.annotate('',v1,v0,arrowprops=arrowprops)  
#描绘数据  
plt.scatter(X[:,0],X[:,1],alpha=0.2)  
  
for length,vector in zip(pca.explained_variance_,pca.components_):  
    v = vector * 3 * np.sqrt(length)  
    draw_vector(pca.mean_,pca.mean_ + v)  
      
plt.axis('equal')

5.基于PCA的降维

1.将n_components设置为1，并使用fit()方法进行拟合

pca=PCA(n_components=1)  
pca.fit(X)

6.降维处理

1.将数据X转换成降维后的数据X_pca，并打印X和X_pca的矩阵形状

X_pca=pca.transform(X)  
  
print("original shape:",X.shape)  
print("transformed shape:",X_pca.shape)

2.使用切片打印X的前十项

X[:10]

3.使用切片打印X_pca的前十项

X_pca[:10]

7.PCA逆向处理

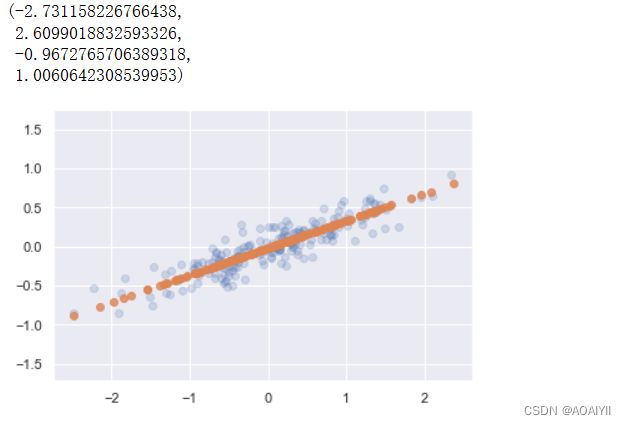
1.将降维后的数据转换成原始数据

X_new=pca.inverse_transform(X_pca)  
#描绘数据  
plt.scatter(X[:,0],X[:,1],alpha=0.2)  
plt.scatter(X_new[:,0],X_new[:,1],alpha=0.8)  
plt.axis('equal')  

8.使用digits.data训练PCA模型并将结果可视化

1.导入sklearn.datasets模块中的load_digits函数

from sklearn.datasets import load_digits  
digits=load_digits()  
#查看digits.data的矩阵形状  
digits.data.shape  

2.使用digits.data训练PCA模型并将结果可视化

pca=PCA().fit(digits.data)  
plt.plot(np.cumsum(pca.explained_variance_ratio_))  
plt.xlabel("number of components")  
plt.ylabel("cumlative explained variance") 

---

总结

主成分分析算法（Principal Component Analysis， PCA）的目的是找到能用较少信息描述数据集的特征组合。它意在发现彼此之间没有相关性、能够描述数据集的特征，确切说这些特征的方差跟整体方差没有多大差距，这样的特征也被称为主成分。这也就意味着，借助这种方法，就能通过更少的特征捕获到数据集的大部分信息。