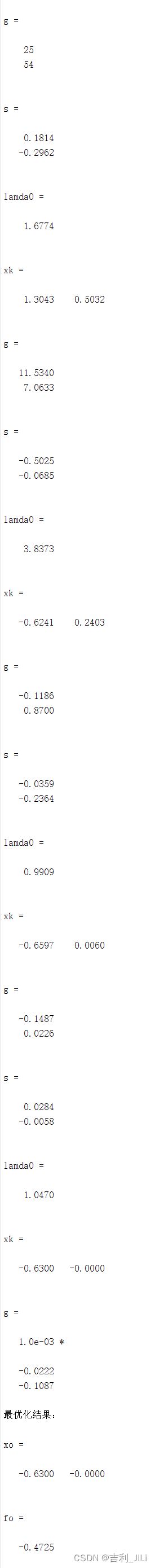基于MATLAB的无约束最优化方法

概述

无约束最优化方法是用于解决无约束函数求最小值问题，其中基本方法有最速下降法、牛顿法、共轭方向法、变尺度法等，而其他方法大多是基本方法的改进。在解决优化问题中，关键在于方向p和步长lambda的选择，不同的方向或步长就构成一种方法。

最速下降法

最速下降法的主要思路：“最好的搜索方向”+“最好的下降步长”

%最速下降法函数
function [xo,fo]=fastest_drop(x0,x,f,e)
syms lamda
df=jacobian(f,x).';
xk=x0;
i=1;
while 1
    d=-subs(df,x,xk).';
    if (d*d')^0.50)
    xk=double(xk+lamda0*d)
    i=i+1;
end
fo=double(subs(f,x,xo));
disp('最优化结果：')

%最速下降法函数测试
clear all;clc;
syms x_1 x_2
f=(x_1-1)^2+(x_2-1)^2;
x0=[515.888,364.15];
x=[x_1,x_2];
[xo,fo]=fastest_drop(x0,x,f,0.1)

程序结果展示：

最速下降法有三个特征：
1、相邻两次迭代的搜索方向互相正交，即锯齿现象。

		  				(g[k])T*（g[k+1]）= 0

2、对二元正定函数，算法产生的点列满足：偶数点列均在一条直线，奇数点列也均在一条直线上，且均过极小点。
3、对二元正定函数，若等值线为圆，则只需一步迭代即可到极小的；若等值线为椭圆，则初始点x1在椭圆长轴/短轴才可一步到极小点，否则发生锯齿现象。
最速下降法的改进方法：
1、采用非精确一维搜索求可接受步长
2、采用固定步长
3、采用加速梯度法：负梯度方向和d[k]=x[k]-x[k-2]结合，交替使用。

牛顿法

牛顿法

牛顿法，由泰勒定理可，迭代公式：

x[k+1]=x[k]-[(▽^2)f(x[k])]^-1*▽f(x[k])

由以上迭代公式可知，牛顿法要求Hessen矩阵(▽^2)f(x[k])正定，以保证可逆且为搜索方向为下降方向

牛顿法的缺点：
1、不具有全局收敛性，收敛于鞍点或极大点的可能并不小；
2、由于涉及函数的一阶导和二阶导，计算量大、存储量大；
3、Hessen矩阵不一定满足正定的条件。

为解决以上缺点，提出了阻尼牛顿法（解决缺点1）、m滞留法（解决缺点2）、G-P法（解决缺点3）和L-M法进行改进（解决缺点3）。

阻尼牛顿法

相对于牛顿法，这里步长不取固定值1，而是采用精确一维搜索步长。

%阻尼牛顿法函数
function [xo,fo]=zuniNewton(x0,x,f,e)
syms lamda
df=jacobian(f,x).';
ddf=jacobian(df.',x);
xk=x0;
while 1
    g=double(subs(df,x,xk))
    if (g.'*g)^0.50))
    xk=double(xk+lamda0*s.')
end
fo=double(subs(f,x,xo));
disp('最优化结果：')

%阻尼牛顿法测试
clear all;clc;
syms x_1 x_2
t1=clock;
f=x_1+(x_2)^2+(x_1)^4+2*x_1^2*x_2^2+8*x_1^2*x_2^6;
%f=-4*x_1+x_1^2+2*x_2^2-2*x_1*x_2;
x0=[1,1];
x=[x_1,x_2];
[xo,fo]=zuniNewton(x0,x,f,0.1)
t2=clock;
etime(t2,t1)

% syms x_1 x_2 x_3
% x=[x_1,x_2,x_3];
% A=[1 1 1;2 3 2;3 3 3];
% b=[2 3 3];
% c=5;
% f=0.5*x*A*x.'+b*x.'+c;
% x0=[5,5,4];
% [xo,fo]=zuniNewton(x0,x,f,0.01)

程序结果展示：

m滞留法

取m∈N+，使得每m次迭代使用同一个Hessen矩阵。

x[k+j+1]=x[k+j]-[(▽^2)f(x[k])]^-1*▽f(x[k+j])
其中，j=0，1，......，m-1
思考：为什么m滞留法采用的是固定步长1，而并非是精确一维搜索？

%m滞留法函数
function [xo,fo]=m_delay(x0,x,f,e,m)
df=jacobian(f,x).';
ddf=jacobian(df.',x);
xk=x0;
j=1;
while 1
    g=double(subs(df,x,xk))
    if (g.'*g)^0.5

%m滞留法函数测试
clear all;clc;
syms x_1 x_2
t1=clock;
f=-4*x_1+x_1^2+2*x_2^2-2*x_1*x_2;
x0=[1,1];
x=[x_1,x_2];
m=5
[xo,fo]=m_delay(x0,x,f,0.1,m)
t2=clock;
etime(t2,t1)

G-P法

若Hessen矩阵正定，搜索方向d[k]=-[(▽^2)f(x[k])]^-1*▽f(x[k]);
否则,d[k]=-▽f(x[k])

并采用非精确一维搜索

L-M法

找到尽可能小的u>0，使得(▽^2)f(x[k])+uI正定；
并用（▽^2)f(x[k])+uI取代（▽^2)f(x[k])

共轭方向法

共轭梯度法

问题的关键在于：寻找搜索方向p[k]

x[k+1]=x[k]+lamda[k]*p[k]           lamda[k]由精确一维搜索得到,(迭代公式)
p[1]=-g[1]
p[k+1]=-g[k+1]+a[k]*p[k]            k=1,2,...,n-1
(g[k+1])T*p[k]=0                    (精确一维搜索性质)
g[k+1]-g[k]=lamda[k]*A*p[K]         (二次函数梯度差)
a[k]=((g[k+1])T*A*p[k])/((p[k])T*A*p[k])

且g[1],g[2],…,g[n]是正交向量组，p[1],p[2],…,p[n]是A共轭向量组。
根据以上公式对a[k]进行变形，不同形式的a[k]对应不同的共轭梯度法，且这些方法同样适用于多维函数。

%共轭梯度法函数
function [xo,fo]=gong_e_direction(x0,x,A,f,n)
syms lamda
df=jacobian(f,x).';
xk=x0;
k=1;
pk1=-double(subs(df,x,xk))
while k0))
    if isempty(lamda0)
        break;
    end
    xk=double(xk+lamda0*pk.')
    dk1=-double(subs(df,x,xk));
    ak=((-dk1).'*A*pk)/(pk.'*A*pk)
    pk1=dk1+ak*pk
    k=k+1
end
xo=xk;
fo=double(subs(f,x,xo));
disp('最优化结果：')

%共轭梯度法函数测试
clear all;clc;
syms x_1 x_2 x_3
x=[x_1,x_2,x_3];
A=[2 0 0;0 1 0;0 0 1];
b=[0 0 0];
c=0;
f=0.5*x*A*x.'+b*x.'+c
x0=[1,1,1];
[xo,fo]=gong_e_direction(x0,x,A,f,size(x,2)+1)

程序结果展示：

以上佐证了对于n维二次函数的最优化问题，采用共轭方向法仅需要n次迭代即可得到最优解。

SW共轭梯度法

a[k]=((g[k+1])T*(g[k+1]-g[k]))/((p[k])T*(g[k+1]-g[k]))

%SW法函数
function [xo,fo]=SW(x1,x,f,e)
syms lamda
n=size(x,2);
df=jacobian(f,x).';
g=double(subs(df,x,x1))
xk=x1;
if (g.'*g)^0.50))
            xk1=double(xk+lamda0*pk.');
            gk1=double(subs(df,x,xk1))
            if (gk1.'*gk1)^0.5

%SW法函数测试
clear all;clc;
syms x_1 x_2
t1=clock;
x=[x_1,x_2];
% f=x_1+(x_2)^2+(x_1)^4+2*x_1^2*x_2^2+8*x_1^2*x_2^6;
% x1=[1,1];
f=1.5*x_1^2+0.5*x_2^2-x_1*x_2-2*x_1;
x1=[-2,4];
[xo,fo]=SW(x1,x,f,0.1)
t2=clock;
etime(t2,t1)

程序结果展示：

DM共轭梯度法

a[k]=-((g[k+1])T*g[k+1])/((p[k])T*g[k])

%DM法函数
function [xo,fo]=SW(x1,x,f,e)
syms lamda
n=size(x,2);
df=jacobian(f,x).';
g=double(subs(df,x,x1))
xk=x1;
if (g.'*g)^0.50))
            xk1=double(xk+lamda0*pk.');
            gk1=double(subs(df,x,xk1))
            if (gk1.'*gk1)^0.5

%DM法函数测试
clear all;clc;
syms x_1 x_2
t1=clock;
x=[x_1,x_2];
% f=x_1+(x_2)^2+(x_1)^4+2*x_1^2*x_2^2+8*x_1^2*x_2^6;
% x1=[1,1];
f=1.5*x_1^2+0.5*x_2^2-x_1*x_2-2*x_1;
x1=[-2,4];
[xo,fo]=SW(x1,x,f,0.1)
t2=clock;
etime(t2,t1)

程序结果展示：

FR共轭梯度法

a[k]=(g[k+1])^2)/(g[k]^2)

%FR法函数
function [xo,fo]=FR(x1,x,f,e)
syms lamda
n=size(x,2);
df=jacobian(f,x).';
g=double(subs(df,x,x1))
xk=x1;
if (g.'*g)^0.50))
            xk1=double(xk+lamda0*pk.');
            gk1=double(subs(df,x,xk1))
            if (gk1.'*gk1)^0.5

%FR法函数测试
clear all;clc;
syms x_1 x_2
t1=clock;
x=[x_1,x_2];
% f=x_1+(x_2)^2+(x_1)^4+2*x_1^2*x_2^2+8*x_1^2*x_2^6;
% x1=[1,1];
f=1.5*x_1^2+0.5*x_2^2-x_1*x_2-2*x_1;
x1=[-2,4];
[xo,fo]=FR(x1,x,f,0.1)
t2=clock;
etime(t2,t1)

程序结果展示：

PPR共轭梯度法

a[k]=((g[k+1])T*(g[k+1]-g[k]))/(g[k]^2)

%PPR函数
function [xo,fo]=PPR(x1,x,f,e)
syms lamda
n=size(x,2);
df=jacobian(f,x).';
g=double(subs(df,x,x1))
xk=x1;
if (g.'*g)^0.50))
            xk1=double(xk+lamda0*pk.');
            gk1=double(subs(df,x,xk1))
            if (gk1.'*gk1)^0.5

%PPR函数测试
clear all;clc;
syms x_1 x_2
t1=clock;
x=[x_1,x_2];
% f=x_1+(x_2)^2+(x_1)^4+2*x_1^2*x_2^2+8*x_1^2*x_2^6;
% x1=[1,1];
f=1.5*x_1^2+0.5*x_2^2-x_1*x_2-2*x_1;
x1=[-2,4];
[xo,fo]=PPR(x1,x,f,0.1)
t2=clock;
etime(t2,t1)

程序结果展示：

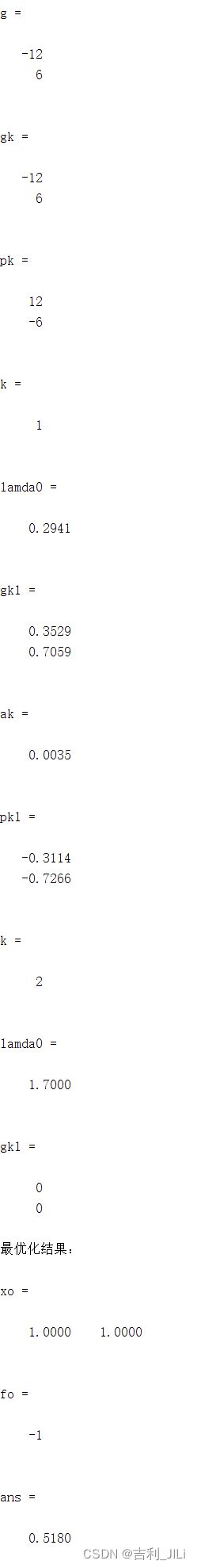
对比程序运行时间，可知PPR的效率更高，而FR形式更为简洁。

变尺度法

为解决牛顿法和阻尼牛顿法中出现的计算量大的问题，采用一个n阶对称正定矩阵H[k]近似代替(▽^2)f(x[k])]^-1
搜索方向是p[k]-H[k]*g[k],H[k]为尺度矩阵。

构造H[k]的原则：

1、拟牛顿性质：△x[k]=H[K+1]*△p[k]
2、二次收敛性
3、稳定性：p[k]为下降方向，即H[K]对称正定。

构造H[k]的一般步骤：
1、H[1]取任意的一个n阶对称正定矩阵，一般取I。
2、修正H[k]，H[k+1]=H[k]+△H[k]
不同的修正矩阵△H[k]，得到不同的变尺度法。

DFR法

△H[k]=(△x[k]*(△x[k])T)/((△x[k])T*△g[k])-(H[k]*△g[k]*(△g[k])T*H[k])/((△g[k])T*H[k]*△g[k])

BFGS法

△B[k]=(△g[k]*(△g[k])T)/((△g[k])T*△x[k])-(B[k]*△x[k]*(△x[k])T*B[k])/((△x[k])T*B[k]*△x[k])
H[k]=(B[k])^-1