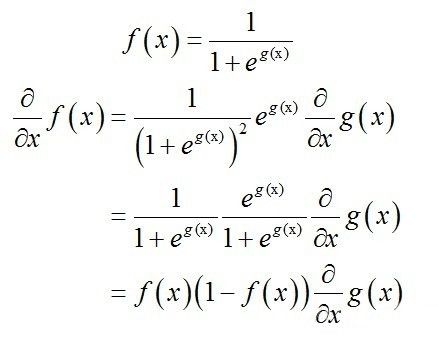Stanford机器学习__Lecture notes CS229. Logistic Regression(逻辑回归)(1)

Stanford机器学习__Lecture notes CS229. Linear Regression(1)

前面这一部分，我们谈了简单线性模型。例如，对于样例(x,y)，当我们希望线性模型的预测值逼近真实标记y时，就得到了线性回归模型，为便于观察，我们把线性回归模型简写成：

y=wT+b

可否令模型预测值逼近y的衍生物？譬如说，假设我们认为示例所对应的输出标记是在指数尺度上变化的，那就可将输出标记的对数作为线性模型逼近的目标，即：

In(y)=wT+b

这就是“对数线性回归（log-linear regression）”，它实际上是在试图让e^{wTx + b}逼近y。对数线性回归实质上已经是在求输入空间到输出空间的非线性函数映射，这里的对数函数起到了将线性回归模型的预测与真是标记联系起来的作用。

（蓝色曲线表示：y = w^Tx + b；绿色曲线表示：y = e^{wTx + b}。）

更一般地，考虑单调可微函数g(.)，令

y=g−1(wT+b)

这样得到的模型称为“广义线性模型”（generalized linear model），其中函数g(.)称为“联系函数”（link function）,显然，对数线性回归是广义线性模型在g(.) = In(.)时的特例。

---

Logistic Regression(逻辑回归)

考虑情况当我们需要根据Tumor(肿瘤)大小来预测肿瘤的良恶性时，假如我们采用简单线性回归的方式：

H(x)=wTx+b

假设，数据集如下：

sizeTumor = [1,2,3,4,5,6,7,8]#瘤子的尺寸
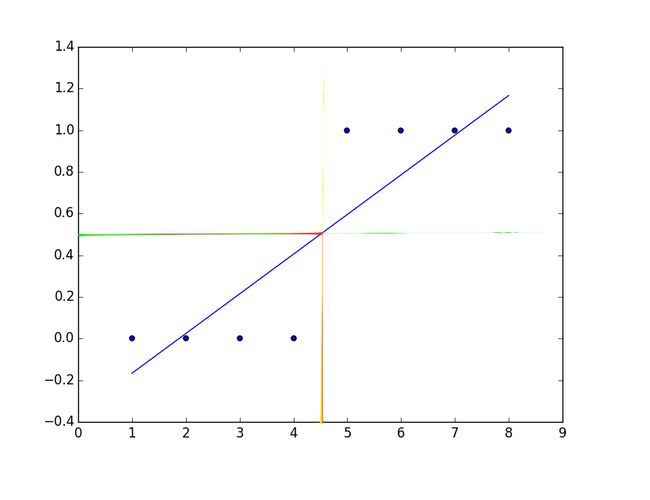
malignant = [0,0,0,0,1,1,1,1]#1:表示为恶性肿瘤，０：表示为良性肿瘤

通过最小二乘法可得：

h(x) = 0.19047619x - 0.35714285714285732

根据图示，我们可以确定一个threshold:0.5进行predict
y=1, if h(x)>=0.5
y=0, if h(x)<0.5

即h(x) = 0.5的点投影下来，其右边的点预测y=1;左边预测y=0；则能够很好地进行分类。

那么由0.5的boundary得到的线性方程中，不能很好地进行分类。因为此时h(x) = 0.49159664，不满足
y=1, h(x)>0.5
y=0, h(x)<=0.5

logistic regression model：

考虑到二分类问题，其输出标记y∈(0,1)，而线性回归模型产生的预测值H(x) = w^Tx + b是实值，于是我们需要将实值H(x)转化为0/1值。最理想的是“单位阶跃函数”（unit-step function）

f(n)=⎧⎩⎨0,0.5,1,h(x) < 0;h(x) = 0 ;h(x) > 0 ;

若观测值h(x) > 0就判定为正例，小雨０则判定为反例，临界值任意判定。

(红色部分表示单位阶跃函数，因其不连续，不能直接用作广义线性模型中的g(.))

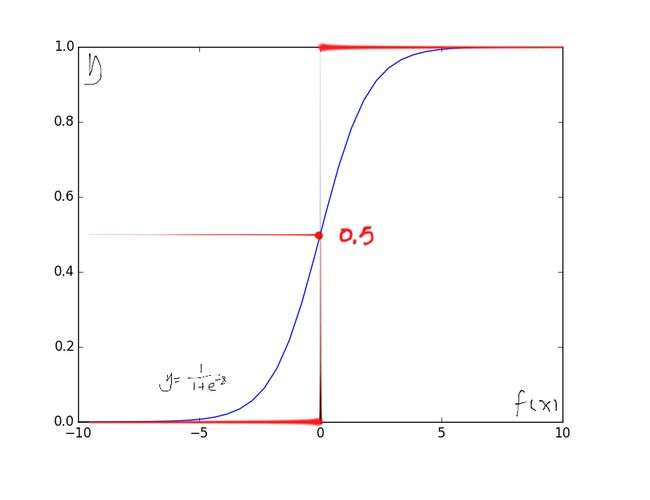
我们希望找到能在一定程度上近似的单位阶跃函数的替代函数，并希望它单调可微。对数几率函数（Logistic functino）就是这样一个常用的函数：

y=11+e−h(x)

从上图中看出，（蓝色曲线）对数几率函数（Logistic functino）是一种“Sigmoid”函数，它将h(x)转化为一个接近0或1的y值，并且其在h(x) = 0附近变化很陡，将对数几率函数（Logistic functino）作为g^-1(.)带入到广义线性模型中，得到：

y=11+e−(wTx+b)

logistic回归实质是一个线性分类模型，它与简单线性回归的不同点在于：为了将线性回归输出的很大范围的数，例如从负无穷到正无穷，压缩到0和1之间，这样的输出值表达为“可能性”才能说服广大民众。当然了，把大值压缩到这个范围还有个很好的好处，就是可以消除特别冒尖的变量的影响（不知道理解的是否正确）。而实现这个伟大的功能其实就只需要平凡一举，也就是在输出加一个logistic函数。另外，对于二分类来说，可以简单的认为：如果样本x属于正类的概率大于0.5，那么就判定它是正类，否则就是负类。

所以说，LogisticRegression 就是一个被logistic方程归一化后的线性回归，仅此而已

需要注意到，虽然它的名字是“回归”，但实际上确实种分类学习方法。这种方法有很多优点，例如它是直接对分类可能性进行建模，无需事先进行假设数据分布，这样就避免了在假设分布不准确带来的问题；它不是仅预测出“类别”，而是可以得到近似概率分布，这对许多利用概率辅助决策的任务很有用；此外对率函数是任意阶可导的凸函数，有很好的数学性质。

logistic方程的求导：
f(x)’ = f(x)(1 - f(x))

若将y视为正样本可能性，则1 - y是其反例可能性。
显然有

p(y=1|x)=e−(wTx+b)1+e−(wTx+b)

p(y=0|x)=11+e−(wTx+b)

根据上面两式，我们可以得到：

p(y|x；Θ)=(1−hΘ(x))1−y(hΘ(x))y

decision boundary

所谓Decision Boundary就是能够将所有数据点进行很好地分类的h(x)边界。
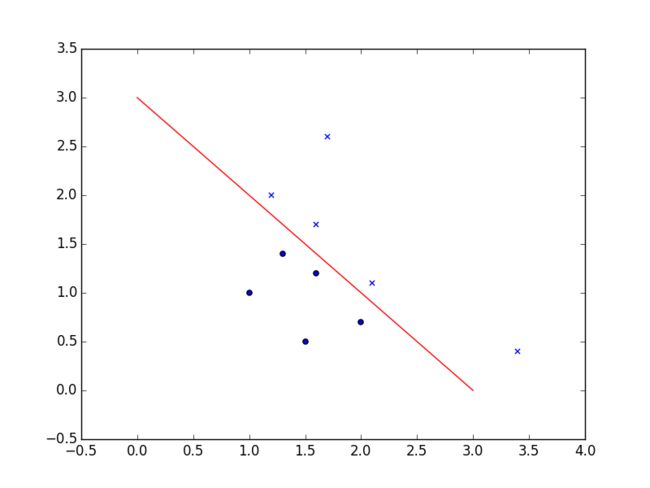
如下图所示，假设形如h(x)=In(θ₀+θ₁x₁+θ₂x₂)的hypothesis参数θ=[-3,1,1]^T, 则有
predict Y=1, if -3+x₁+x₂ >= 0
predict Y=0, if -3+x₁+x₂ < 0

刚好能够将图中所示数据集进行很好地分类:

除了线性boundary还有非线性decision boundaries，如图所示,假设形如h(x)=In(θ₀+θ₁x₁+θ₂x₂+θ₃x₃²+θ₄x₄²)的hypothesis参数θ=[-1,0,0,1,1]^T, 则有
predict Y=1, if -1+x₁²+x₂²>=0
predict Y=0, if -1+x₁²+x₂²<0

刚好能够将图中所示数据集进行很好地分类

Cost function for logistic regression

假设我们有需要做分类的训练集{(x₁,y₁),(x₂,y₂)……(x_m,y_m)}
x_i ϵ Rⁿ，且x_i0 = 1，y_i ϵ (0,1);

h(x)=11+e−(wTx+b)

这里我们要怎样选择w才能得到合适的decision boundary呢？
我们已知简单线性回归使用一下的cost function来计算适合的w

J(Θ)=1m∑i=1m12(h(x(i))Θ−y(i))2，简单线性回归's cost function

为了一般化cost function:
我们将误差项的平方记为：cost()
写作：

cost(h(x(i))Θ,y(i))=12(h(x(i))Θ−y(i))2，评估了第i个用例的误差

于是，我们重定义了cost function（在得到Logistic Regression的cost fucntion之前，我们权且记作）:

J(Θ)=1m∑i=1mcost(h(x(i))Θ,y(i))

当我们的hypothesis中使用了sigmoid函数，导致我们不能再使用像简单线性回归那样的cost function，因为这时它的cost function不是一个凸函数（这就意味着会有许多的局部极小值阻碍我们到达全局最小值）
相信看过Stanford机器学习__Lecture notes CS229. Linear Regression(2)
都还会有印象，即使我们的简单线性回归的cost function也不是平白无故得来的，我们在上述的blog中用极大似然估计解释了简单线性回归以估计与真实值的平方差的和为cost function的原因。

A convex logistic regression cost function

我们需要一个可以应用梯度下降的作为凸函数的cost function:

Cost(h(x(i))Θ,y(i))={−log(hΘ(x)),−log(1−hΘ(x)),if y = 1;if y = 0 ;

让我们先简单定性地分析一下cost funciton。（以y等于1为例）

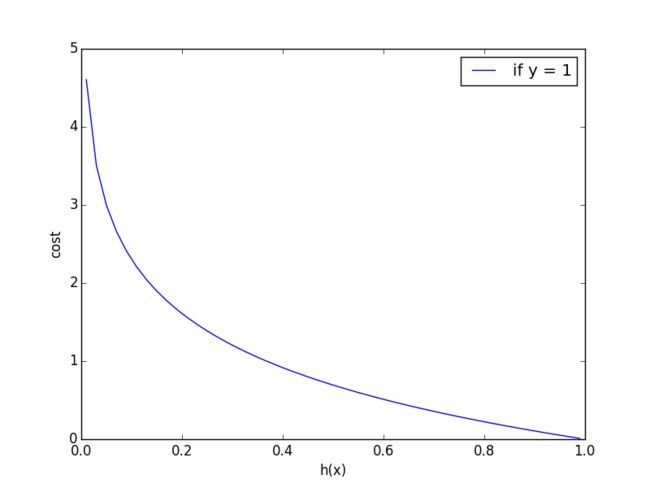
当我们完全正确的时候，cost等于0。
当我们越来越偏离正确答案的时候，cost会越来越大。
符合我们的认识。
我们可以得到：

cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))

Simplified cost function and gradient descent

我们按照之前的方法，利用最大似然来解释这个cost function由来。

假设我们有n个独立的训练样本{(x₁, y₁) ,(x₂, y₂),…, (x_n, y_n)}，y={0, 1}。那每一个观察到的样本(xi, yi)出现的概率是：

p(y|x；Θ)=(1−hΘ(x))1−y(hΘ(x))y

那我们的整个样本集，也就是n个独立的样本出现的似然函数为（因为每个样本都是独立的，所以n个样本出现的概率就是他们各自出现的概率相乘）：

L(Θ)=∏i=1n(1−hΘ(x))1−yi(hΘ(x))yi

那最大似然法就是求模型中使得似然函数最大的系数取值Θ。这个最大似然就是我们的代价函数（cost function）了。

我们对L(Θ)取log。

如果取log以后求偏导等于0，有解的话，就说明有这个解的时候，我们能一步到位。而需要通过迭代了，耗时耗力。但很遗憾对下式无法解析求解

最大似然估计就是要求得使l(θ)取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。其实我们时需要在前面乘上一个系数就能转化为梯度下降法求解。

J(Θ)=−1mL(Θ)

因为乘了一个负的系数-1/m，所以J(θ)取最小值时的θ为要求的最佳参数。

梯度下降法求J(θ)的最小值。

求J(θ)的最小值可以使用梯度下降法，根据梯度下降法可得θ的更新过程：

θjnew=θjold−α∂∂θjJ(θ),(j = 0,1,2...n)

已知：

则，对θ_j求其偏导可得：

故，我们的梯度下降的更新过程可以写作：

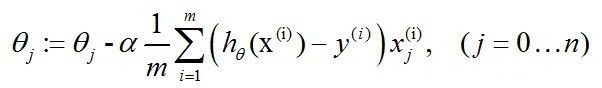
因为式中α本来为一常量，所以一般将1/m省略。

事实上，当我们用梯度上升算法求取最大值的时候，我们会发现：

最后得到的更新方程跟梯度下降法得到的是一样的。

根据最后的推导结果我们可以发现，不管h(x)的表达式是线性的还是logistic regression model, 都能得到如下的参数更新过程：

θjnew=θjold−α∑j=1n(hθ(x(i)－y(i)))x(i)j,text(j=0,1,2...n)

简单应用：

这里依然举肿瘤的例子：
批量梯度下降代码：https://code.csdn.net/snippets/1867776.git

最后得到的分类点。

每个example的error的变化情况。

θ1的变化情况

θ0的变化情况

随机梯度下降代码：[email protected]:snippets/1867787.git

θ1的变化情况（局部）

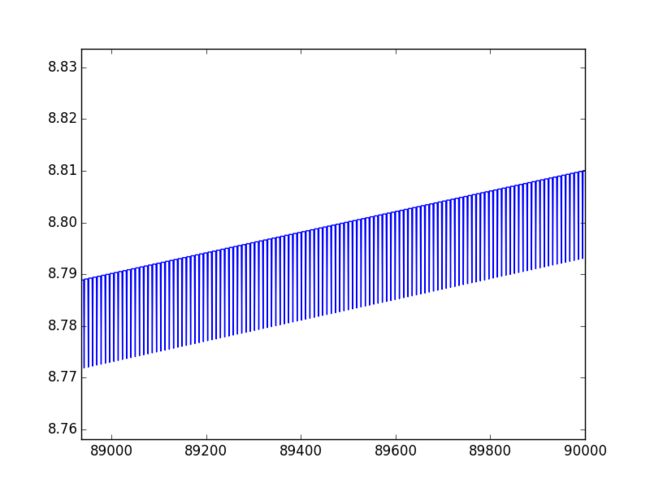
我们可以看到这里存在局部波动的现象。
仔细观察我们可以发现，这些波动存在着一定的周期性。
不难理解，产生这类波动的原因是存在一些不能正确分类的样本点，在每次迭代的时候会引发系数的剧烈变化。
我们可以对代码做出一些修改来尽可能避免这样的波动。

改进以后的随机梯度下降代码：[email protected]:snippets/1868132.git

θ1的变化情况（局部）

这里的改进主要表现在两个地方。
一个方面，alpha在每次迭代的时候都会调整，这会缓解之前的数据波动或者高频波动。另外，虽然alpha会随着迭代次数的不断减小，但永远不会减小到0，这是因为alpha中依然保存着一个常数项。必须这么做的原因是为了保证在多次迭代以后新数据任然具有一定的影响。如果要处理的问题是动态变化的，那么就要适当地加大上述的常数项，来确保新的值后的更大的回归悉数。同时需要注意的是，在降低alpha每次减小1/(i+j)。其中j是迭代次数，i是样本下标。这样当j远远小于max(i)时，alpha就不生严格下降的。避免参数的严格下降也常见于模拟退货算法等其他优化算法中。
另一方面：我们在改进以后的随机梯度下降法中每次用于更新回归参数的样本实际上是随机从样本中选取出来的。这种方法将减少周期性的波动。

小节：

同之前的简单回归，由于批量梯度上升算法在更新回归系数时需要遍历整个数据集，所以该方法在处理100个样本时表现上课，但如果有数十亿个样本和成千上万的特征，那样复杂度就太高了。基于此我们引入了随机梯度下降算法。但随机梯度算法由于一些不能正确分类的样本点的存在（数据集并非线性可分），进而每次迭代都会印发系数的剧烈变动。而使用样本随机选择和alpha动态减少机制的随机梯度下降算法会比固定alpha的方法收敛速度更快。

参考博客：

http://feature-space.com/2011/10/28/logistic-cost-function-derivative/
http://www.holehouse.org/mlclass/06_Logistic_Regression.html