花书学习笔记--神经网络实践方法论

目录

性能度量

准确率

查准率precision和召回率recall

覆盖（ coverage）

基准模型

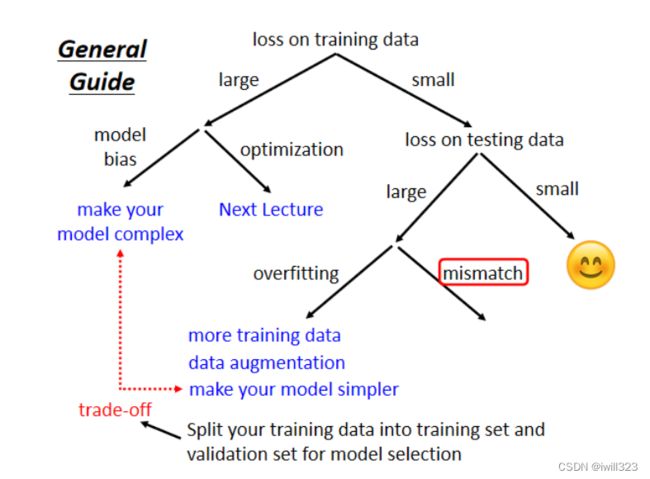
如何判断遇到的是什么问题

Model Bias（模型偏差）

Optimization Issue（没做好优化）

Overfitting（过拟合）

如何解决过拟合

是否收集更多数据

Trade-off（如何权衡模型的复杂程度）

为什么用了验证集结果还是过拟合了

N-fold Cross Validation

Mismatch

选择超参数

手动调整超参数

自动超参数优化算法

网格搜索

随机搜索

网格搜索和随机搜索的比较

调试策略

---

在机器学习系统的日常开发中，实践者需要决定是否收集更多的数据、增加或减少模型容量、添加或删除正则化项、改进模型的优化、改进模型的近似推断或调试模型的软件实现。尝试这些操作都需要大量时间，因此确定正确做法，而不盲目猜测尤为重要
参考以下几个实践设计流程：

• 确定目标——使用什么样的误差度量，并为此误差度量指定目标值。这些目标和误差度量取决于该应用旨在解决的问题。
• 尽快建立一个端到端的工作流程，包括估计合适的性能度量。
• 搭建系统，并确定性能瓶颈。检查哪个部分的性能差于预期，以及是否是因为过拟合、 欠拟合，或者数据或软件缺陷造成的。
• 根据具体观察反复地进行增量式的改动，如收集新数据、调整超参数或改进算法。

性能度量

最重要的是首先要确定改进哪个性能度量，然后专心提高性能度量。如果没有明确的目标，那么我们很难判断机器学习系统上的改动是否有所改进。
对于大多数应用而言，不可能实现绝对零误差。即使你有无限的训练数据，并且恢复了真正的概率分布， 贝叶斯误差仍定义了能达到的最小错误率。这是因为输入特征可能无法包含输出变量的完整信息，或是因为系统可能本质上是随机的。当然我们还会受限于有限的训练数据。
如何确定合理的性能期望？在学术界，通常我们可以根据先前公布的基准结果来估计预期错误率。在现实世界中，一个应用的错误率有必要是安全的、具有成本效益的或吸引消费者的。

准确率

我们通常会度量一个系统的准确率，或等价地， 错误率。
有时，一种错误可能会比另一种错误更严重。例如，垃圾邮件检测系统会有两种错误：将正常邮件错误地归为垃圾邮件，将垃圾邮件错误地归为正常邮件。阻止正常消息比允许可疑消息通过糟糕得多。我们希望度量某种形式的总代价，其中拦截正常邮件比允许垃圾邮件通过的代价更高，而不是度量垃圾邮件分类的错误率。

查准率precision和召回率recall

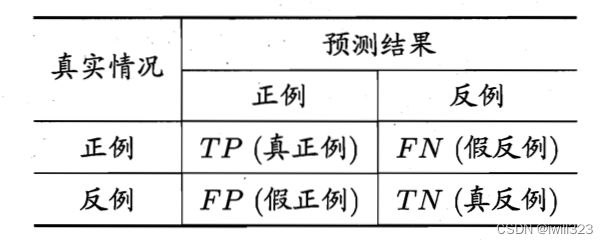
有时，我们需要训练检测某些罕见事件的二元分类器。解决这个问题的方法是度量查准率precision和召回率recall。查准率是模型报告的检测是正确的比率，而召回率则是真实事件被检测到的比率。比如为一种罕见疾病设计医疗测试，检测器永远报告没有患者，会得到一个完美的精度，但召回率为零。而报告每个人都是患者的检测器会得到一个完美的召回率，但是精度会等于人群中患有该病的比例。

precision = TP/(TP + FP)代表了模型做出正例预测时正确的概率

recall = TP/(TP + FN)代表了对于所有实际上正确的例子，模型检测到的比例

当使用精度和召回率时，我们通常会画 PR 曲线（ PR curve）， y 轴表示精度， x 轴表示召回率。在很多情况下，我们希望用一个数而不是曲线来概括分类器的性能。例如，我们将前馈网络设计为检测一种疾病，估计一个医疗结果由特征 x 表示的人患病的概率为 y^ = P (y = 1 | x)。每当这个得分超过某个阈值时，我们报告检测结果。通过调整阈值，我们能权衡精度和召回率。要做到这一点，我们可以将精度 p 和召回率 r 转换为 F 分数（ F-score）

 另一种方法是报告 PR 曲线下方的总面积

覆盖（ coverage）

在一些应用中， 机器学习系统可能会拒绝做出判断。特别是在错误判断会导致严重危害，而人工操作员能够偶尔接管的情况下，如果机器学习算法能够估计所作判断的置信度，这将会非常有用。当然，只有当机器学习系统能够大量降低需要人工操作处理的图片时，它才是有用的。在这种情况下，一种自然的性能度量是 覆盖（ coverage）。 覆盖是机器学习系统能够产生响应的样本所占的比率。我们权衡覆盖和精度。一个系统可以通过拒绝处理任意样本的方式来达到 100% 的精度，但是覆盖降到了 0%。对于街景任务，该项目的目标是达到人类级别的转录精度，同时保持 95% 的覆盖。在这项任务中，人类级别的性能是 98% 的精度

基准模型

确定性能度量和目标后，任何实际应用的下一步是尽快建立一个合理的端到端的系统。
首先，根据数据的结构选择一类合适的模型。

• 如果项目是以固定大小的向量作为输入的监督学习，那么可以使用全连接的前馈网络。
• 如果输入有已知的拓扑结构（例如，输入是图像），那么可以使用卷积网络。在这些情况下，刚开始可以使用某些分段线性单元（ ReLU 或者其扩展，如 Leaky ReLU、 PReLU 和 maxout）。
• 如果输入或输出是一个序列，可以使用门控循环网络（ LSTM 或 GRU）。

模型中可以采取优化措施

• 具有衰减学习率以及动量的 SGD 是优化算法一个合理的选择（可以采取衰减方法）。另一个非常合理的选择是 Adam 算法。
• 批标准化对优化性能有着显著的影响，特别是对卷积网络和具有 sigmoid 非线性函数的网络而言。虽然在最初的基准中忽略批标准化是合理的，然而当优化似乎出现问题时，应该立刻使用批标准化。
• 除非训练集包含数千万以及更多的样本，否则项目应该在一开始就包含一些温和的正则化。 提前终止也被普遍采用。 Dropout 也是一个很容易实现，且兼容很多模型和训练算法的出色正则化项。 批标准化有时也能降低泛化误差，此时可以省略 Dropout 步骤，因为用于标准化变量的统计量估计本身就存在噪声。
• 如果我们的任务和另一个被广泛研究的任务相似，那么通过复制先前研究中已知性能良好的模型和算法，可能会得到很好的效果。甚至可以从该任务中复制一个训练好的模型。例如，通常会使用在 ImageNet 上训练好的卷积网络的特征来解决其他计算机视觉任务

一个常见问题是项目开始时是否使用无监督学习，这个问题和特定领域有关。在某些领域，比如自然语言处理，能够大大受益于无监督学习技术，如学习无监督词嵌入。在其他领域，如计算机视觉，除非是在半监督的设定下（ 标注样本数量很少），目前无监督学习并没有带来益处。如果应用所在环境中， 无监督学习被认为是很重要的，那么将其包含在第一个端到端的基准中。否则，只有在解决无监督问题时，才会第一次尝试时使用无监督学习。在发现初始基准过拟合的时候，我们可以尝试加入无监督学习

如何判断遇到的是什么问题

Model Bias（模型偏差）

在训练过程中的 loss 就很大时，有可能是发生了 model bias 的问题。Model Bias 的意思就是适用的模型太简单了，不足以让 loss 足够低，也就是太简单的模型没法精确描述复杂的问题。

解决方案：调整模型，让模型变复杂变得有弹性，使模型能够包含更多情况。使模型变复杂的方法：1、使用更多的特征作为自变量。2、加深神经网络，用到更多的神经元和层数。

Optimization Issue（没做好优化）

Optimization Issue 是指我们猜测的含未知参数的模型是好的，里面包含能使 loss 低的可能，但是没有找到使 loss 低的最佳参数。最典型的就是 gradient descent 遇到了局部最小值，没有找到能使 loss 很小的参数。

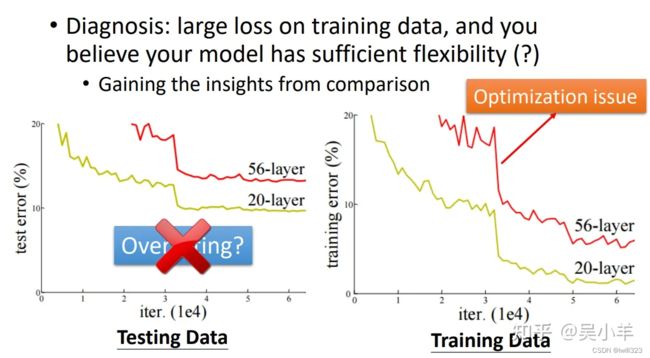
以下面的实验结果图为例，右边的 56层神经网络在训练资料上的 loss 很大，是优化问题而不是 model bias问题。model bias 是因为模型太简单导致 loss 大，假如 56层是 model bias 的问题，那么比 56层更简单的 20层的 loss应该更大，因为 20层的弹性更小，更不能描述复杂问题。可是20层的 loss 比 56层的 loss要低，所以56层的网络是由于没有做好优化导致 loss 偏高。

怎么判断优化有没有做好呢？

首先训练浅层的神经网络，或者是简单的模型（linear model、support vector machine）；然后再去训练深层的网络，如果深层的网络不能比浅层的网络获得更低的训练 loss ，那么深层网络的优化就没有做好，还得继续优化。

Overfitting（过拟合）

在训练资料上的表现很好，但是放在测试资料上结果就一塌糊涂，loss 很大，那么就是过拟合问题。过拟合的原因就是实验者为了逼近训练资料而拟合，眼睛里只有training loss 要小，导致使用了过于复杂的模型，虽然该模型能很好地吻合训练资料的分布，但是该模型却并不符合真实分布。

如何解决过拟合

1、搜集更多的训练资料，或创造新资料，但是资料要合理，要根据domain knowledge来创造。 比如data augmentation
2、给模型一些限制，使用更少的自变量，使用更少的参数。

要用多constrain的model才会好，取决于对这个问题的理解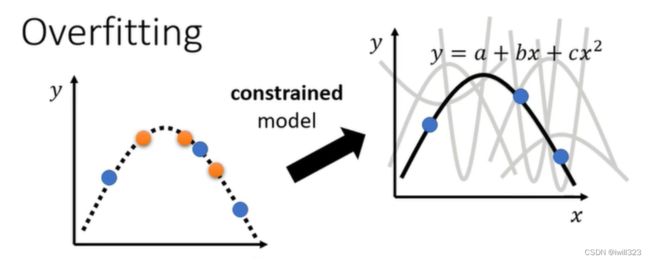

假设已经知道模型是二次曲线，就会在选择function的时候，有很大的限制，因為二次曲线来来去去就是那几个形状而已，只能够选那几个function，虽然说只给了三个点，但是因為我们能选择的function有限，可能就会正好选到跟真正的distribution比较接近的function，然后在测试集上得到比较好的结果。

3、在 CNN 中还会用到共享参数的做法

花书说，“可以把卷积网络类比成全连接网络，但对于这个全连接网络的权重有一个无限强的先验，这个先验说明了该层应该学得的函数只包含局部连接关系（稀疏权重）并且对平移具有等变性”。可以将先验理解为上一条说的“constraint”

4、early stopping、regularization、dropout

是否收集更多数据

首先，确定训练集上的性能是否可接受。如果模型在训练集上的性能就很差，学习算法都不能在训练集上学习出良好的模型，那么就没必要收集更多的数据。如果更大的模型和仔细调试的优化算法效果不佳，那么问题可能源自训练数据的质量。数据可能含太多噪声，或是可能不包含预测输出所需的正确输入。这意味着需要重新开始，收集更干净的数据或是收集特征更丰富的数据集。
如果训练集上的性能是可接受的，且测试集上的性能比训练集的要差得多，那么收集更多的数据是最有效的解决方案之一。这时主要的考虑是收集更多数据的代价和可行性，其他方法降低测试误差的代价和可行性，和增加数据数量能否显著提升测试集性能。一个可以替代的简单方法是降低模型大小或是改进正则化（调整超参数，如权重衰减系数，或是加入正则化策略，如 Dropout）。如果调整正则化超参数后， 训练集性能和测试集性能之间的差距还是不可接受，那么收集更多的数据是可取的。
在决定是否收集更多的数据时，也需要确定收集多少数据。绘制曲线显示训练集规模和泛化误差之间的关系是很有帮助的（下图）。根据走势延伸曲线，可以预测还需要多少训练数据来达到一定的性能。通常，加入总数目一小部分的样本不会对泛化误差产生显著的影响。因此，建议在对数尺度上考虑训练集的大小，例如在后续的实验中倍增样本数目。

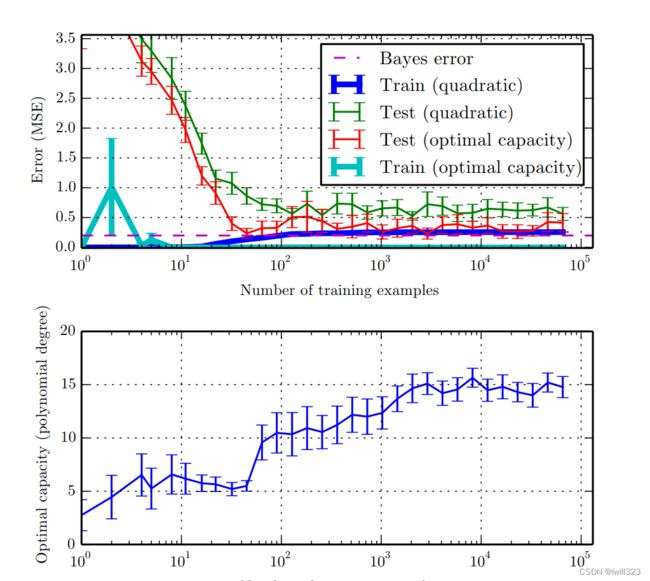
如果收集更多的数据是不可行的，那么改进泛化误差的唯一方法是改进学习算法本身。这属于研究领域，并非对应用实践者的建议。

Trade-off（如何权衡模型的复杂程度）

产生了model bias 问题就想增加模型复杂度，产生了overfitting 问题就想降低模型复杂度，这其中就存在一个权衡，那我们要怎么选择合适的模型，既不会太复杂也不会太简单？可以将训练资料分成训练集和验证集，根据验证集的结果去挑模型。

为什么用了验证集结果还是过拟合了

用验证集挑选模型的过程其看作是一种在验证集上的训练，在验证集上挑选的模型多了，就可能导致过拟合。假设现在有一群模型，它们会做的事情就是训练集裡面有的资料就把它记下，训练集没看过的东西就直接输出随机的结果。虽然说每一个模型在testing data上面输出的结果都是随机的，但是不断的随机，某个模型找出来的函数正好在testing data上面，就给出一个好的结果。但是这个模型毕竟是随机的，它在private testing set上很难表现好。我们训练出一个模型放到public set上以后，发现结果不好，然后去调整模型，假设这一个route做太多次，就有可能fit在public Testing Set上面。所以根据验证集的结果挑模型，不要去管public Testing Set的结果。

N-fold Cross Validation

假如想避免验证集的偶然性，可以采取N-fold Cross Validation：将训练资料分成三份A、B、C，同一个模型做三次试验，分别选用A、B、C作为验证集。最后将三次试验的平均 loss 作为该模型的 loss，通过这个平均 loss 去挑选模型。

Mismatch

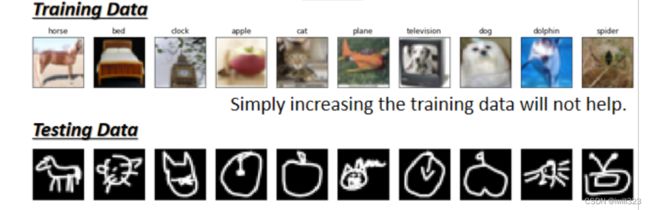
训练资料上表现好，而测试资料上表现差的一种可能是过拟合，另一种可能是 mismatch。

mismatch 就是训练资料和测试资料有着不同的分布。简单地增加训练资料对这个问题是没有帮助的，增加资料只能降低 training loss 而不能降低 testing loss，因为两笔资料产生方式不同，就不能通过training data的规律去预测testing data的规律。

选择超参数

有些超参数会影响算法运行的时间和存储成本。有些超参数会影响学习到的模型质量，以及在新输入上推断正确结果的能力。
有两种选择超参数的基本方法：手动选择和自动选择。手动选择超参数需要了解超参数做了些什么，以及机器学习模型如何才能取得良好的泛化。自动选择超参数算法大大减少了解这些想法的需要，但它们往往需要更高的计算成本。

手动调整超参数

手动搜索超参数的目标通常是最小化泛化误差。
手动搜索超参数的主要目标是调整模型的有效容量以匹配任务的复杂性。有效容量受限于三个因素：模型的表示容量、学习算法最小化代价函数的能力以训练过程正则化模型的程度。具有更多网络层，每层有更多隐藏单元的模型具有较高的表示能力——能够表示更复杂的函数。然而，如果训练算法不能找到某个合适的函数来最小化训练代价，或是正则化项（如权重衰减）排除了这些合适的函数，那么即使模型的表达能力较高，也不能学习出合适的函数。
当泛化误差以某个超参数为变量，作为函数绘制出来时，通常会表现为 U 形曲线。学习率可能是最重要的超参数。当学习率大于最优值时误差会有显著的提升。当学习率太小，训练不仅慢，还有可能永久停留在一个很高的训练误差。泛化误差也会得到类似的曲线。由于一个糟糕的优化从某种程度上说可以避免过拟合，即使是训练误差相同的点也会拥有完全不同的泛化误差。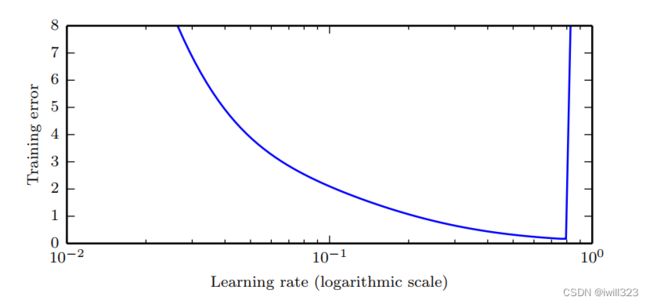

调整学习率外的其他参数时，需要同时监测训练误差和测试误差，以判断模型是否过拟合或欠拟合，然后适当调整其容量。

如果训练集错误率大于目标错误率，那么只能增加模型容量以改进模型。如果没有使用正则化，并且确信优化算法正确运行，那么有必要添加更多的网络层或隐藏单元。然而，令人遗憾的是，这增加了模型的计算代价。
如果测试集错误率大于目标错误率，当训练误差较小（因此容量较大），可以改变正则化超参数，以减少有效的模型容量，如添加 Dropout 或权重衰减策略。通常，最佳性能来自正则化得很好的大规模模型，比如使用 Dropout 的神经网络。
大部分超参数可以通过推理其是否增加或减少模型容量来设置。部分示例如表所示。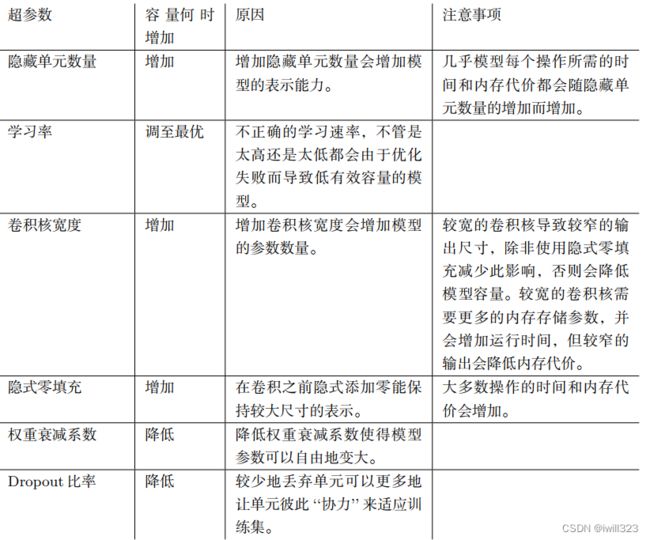

实践中能够确保学习有效的暴力方法就是不断提高模型容量和训练集的大小，直到解决问题。这种做法增加了训练和推断的计算代价，所以只有在拥有足够资源时才是可行的。原则上，这种做法可能会因为优化难度提高而失败，但对于许多问题而言，优化似乎并没有成为一个显著的障碍，当然，前提是选择了合适的模型。

自动超参数优化算法

网格搜索

当有三个或更少的超参数时，常见的超参数搜索方法是 网格搜索（ grid search）。对于每个超参数，使用者选择一个较小的有限值集去探索。然后，这些超参数笛卡尔乘积得到一组组超参数， 使用每组超参数训练模型，挑选验证集误差最小的超参数作为最好的超参数。

应该如何选择搜索集合的范围呢？在超参数是数值（有序）的情况下，每个列表的最小和最大的元素可以基于先前相似实验的经验保守地挑选出来，以确保最优解非常可能在所选范围内。通常， 网格搜索大约会在 对数尺度（ logarithmic scale）下挑选合适的值，例如，一个学习率的取值集合是 {0.1, 0.01, 10-3, 10-4, 10-5}，或者隐藏单元数目的取值集合 {50, 100, 200, 500, 1000, 2000}

通常重复进行网格搜索时，效果会最好。例如，假设我们在集合 {-1, 0, 1} 上网格搜索超参数 α。如果找到的最佳值是 1，那么说明我们低估了最优值 α 所在的范围，应该改变搜索格点，例如在集合 {1, 2, 3}中搜索。如果最佳值是 0，那么我们不妨通过细化搜索范围以改进估计，在集合{-0.1, 0, 0.1}上进行网格搜索。

网格搜索带来的一个明显问题是，计算代价会随着超参数数量呈指数级增长。如果有 m 个超参数，每个最多取 n 个值，那么训练和估计所需的试验数将是 O()。可以并行地进行实验，并且并行要求十分宽松（进行不同搜索的机器之间几乎没有必要进行通信）。令人遗憾的是，由于网格搜索指数级增长计算代价，即使是并行，也无法提供令人满意的搜索规模

随机搜索

有一个替代网格搜索的方法，并且编程简单，使用更方便，能更快地收敛到超参数的良好取值： 随机搜索。
随机搜索过程如下。首先，为每个超参数定义一个边缘分布，例如， Bernoulli分布或范畴分布（分别对应着二元超参数或离散超参数），或者对数尺度上的均匀分布（对应着正实值超参数）。例如，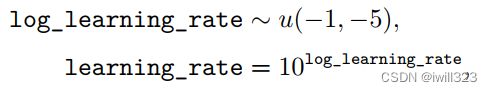

其中， u(a, b) 表示区间 (a, b) 上均匀采样的样本。类似地， log_number_of_hidden_units可以从 u(log(50), log(2000)) 上采样
与网格搜索不同，我们不需要离散化超参数的值。这允许我们在一个更大的集合上进行搜索，而不产生额外的计算代价。当有几个超参数对性能度量没有显著影响时， 随机搜索相比于网格搜索指数级地高效，能够更快地减小验证集误差（就每个模型运行的试验数而言）。
与网格搜索一样，我们通常会重复运行不同版本的随机搜索，以基于前一次运行的结果改进下一次搜索。

网格搜索和随机搜索的比较

为了方便地说明，只展示两个超参数的例子，但是关注的问题中超参数个数通常会更多。 (左) 为了实现网格搜索，为每个超参数提供了一个值的集合。搜索算法对每一种超参数组合进行训练。 (右) 为了实现随机搜索，给联合超参数赋予了一个概率分布。通常超参数之间是相互独立的。常见的这种分布的选择是均匀分布或者是对数均匀的。搜索算法从联合的超参数空间中采样，然后运行每一个样本。

这个图说明了通常只有一个超参数对结果有着重要的影响。在这个例子中，只有水平轴上的超参数对结果有重要的作用。网格搜索将大量的计算浪费在了对结果无影响的超参数中，有时会对一个超参数的两个不同值给出相同结果，而其他超参数将在这两次实验中拥有相同的值。如果这两个值的变化所对应的验证集误差没有明显区别的话， 没有必要重复两个等价的实验，随机搜索几乎每次都测试了每个超参数的独一无二的值，所以更加高效。

调试策略

• 可视化计算中模型的行为：模型的单一数字化指标例如accuracy常常会隐藏一些问题而且无法直观的看出模型效果，这时我们有必要利用可视化方法来帮助理解，例如图像识别时可以将模型识别的物体叠加显示在原图上
• 可视化最严重的错误：大多数模型能够输出运行任务时的某种置信度量。例如，基于 softmax 函数 输出层的分类器给每个类分配一个概率，给出了模型在其分类决定上的置信估计值。可视化不正确而模型给了最高置信度的训练集转录结果，通常可以发现该数据预处理或者标记方式的问题。
• 根据训练和测试误差检测程序：如果训练误差较低，但是测试误差较高，那么很有可能过拟合了。另一种可能是， 测试误差没有被正确地度量，可能是由于训练后保存模型再重载去度量测试集时出现问题，或者是因为测试数据和训练数据预处理的方式不同。如果训练和测试误差都很高，那么很难确定是程序错误，还是由于算法原因模型欠拟合。这种情况需要进一步的测试，如下面所述。
• 拟合极小的数据集：当训练集上有很大的误差时，需要确定问题是真正的欠拟合，还是程序错误。通常，即使是小模型也可以保证很好地拟合一个足够小的数据集。通常，如果不能训练一个分类器来正确标注一个单独的样本，或不能训练一个自编码器成功地再现一个单独的样本，那么很有可能是软件错误导致训练集上的误差。
• 比较反向传播导数和数值导数：如果读者正在使用一个需要实现梯度计算的软件框架，或者在添加一个新操作到求导库中，必须定义它的 bprop 方法，那么常见的错误原因是没能正确地实现梯度表达。验证这些求导正确性的一种方法是比较实现的自动求导和通过 有限差分（ finite difference）计算的导数。扰动大小 ϵ 必须足够大，以确保该扰动不会由于数值计算的有限精度问题产生舍入误差。对于向量值函数，令人遗憾的是， 有限差分只允许我们每次计算一个导数。我们可以使用有限差分 mn 次评估g 的所有偏导数，也可以将该测试应用于一个新函数（在函数的输入输出都加上随机投影）。
• 监控激活函数值和梯度的直方图：大量训练迭代后（也许是一个epoch)， 隐藏单元的预激活值可以告诉我们该单元是否饱和，或者它们饱和的频率如何，梯度是消失还是爆炸。例如，对于ReLu，它们多久关一次？是否有单元一直关闭？比较参数梯度和参数的量级，我们希望参数在一个小批量更新中变化的幅度是参数量值 1% 这样的级别，而不是 50% 或者 0.001%（这会导致参数移动得太慢）。也有可能是某些参数以良好的步长移动，而另一些停滞。如果数据是稀疏的（比如自然语言），有些参数可能很少更新，检测它们变化时应该记住这一点。