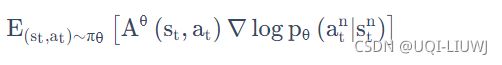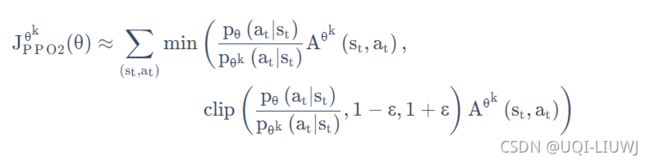强化学习笔记：PPO 【近端策略优化（Proximal Policy Optimization）】

1 前言

我们回顾一下policy network：

强化学习笔记：Policy-based Approach_UQI-LIUWJ的博客-CSDN博客

         

        它先去跟环境互动，搜集很多的 路径τ。根据它搜集到的路径，按照 policy gradient 的式子去更新 policy 的参数。

         但问题是，一旦我们更新了参数，从θ变成了θ'，那么这个概率就不对了，之前采样出来的数据就变的不能用了。

         所以 policy gradient 是一个会花很多时间来采样数据的算法，大多数时间都在采样数据，agent 去跟环境做互动以后，接下来就要更新参数。你只能更新参数一次。接下来你就要重新再去收集数据， 然后才能再次更新参数。这显然是非常花时间的。

   于是就有了PPO算法：用另外一个 policy， 另外一个 actorθ′ 去跟环境做互动(θ′ 固定)。用θ′ 收集到的数据去训练θ。

        假设我们可以用θ′ 收集到的数据去训练 θ，意味着说我们可以把θ′ 收集到的数据用非常多次，我们可以执行梯度上升(gradient ascent)好几次，我们可以更新参数好几次， 都只要用同一笔数据就好了。

        因为假设θ 有能力学习另外一个 actorθ′ 所采样出来的数据的话， 那θ′ 就只要采样一次，采样多一点的数据， 让θ 去更新很多次，这样就会比较有效率。

2 重要性采样 

数学笔记：重要性采样_UQI-LIUWJ的博客-CSDN博客

3 PPO

3.1 重要性权重

        采用重要性采样的思路，我们现在的 τ 是从θ′ 采样出来的，是拿θ′ 去跟环境做互动。所以采样出来的τ 是从θ′ 采样出来的，这两个分布不一样。但没有关系，和重要性采样一样，我们补上一个重要性权重

        这一项是很重要的，因为你要学习的是 θ ，和θ′ 是不太一样的：'θ′ 会见到的情形跟 θ 见到的情形不见得是一样的，所以中间要做一个修正的项。

 3.2 θ替换成θ’有什么好处？

        现在跟环境做互动是θ′ 而不是θ。所以采样出来的东西跟θ 本身是没有关系的。

        所以可以让θ′ 做互动采样一大堆的数据，然后θ 可以根据采样得到的这一大堆数据，更新参数很多次，一直到θ 训练到一定的程度，更新很多次以后，θ′ 再重新去做采样——>这样可以省下很多的采样时间

3.3 回顾：policy-based approach的policy gradient

        在做 policy gradient 的时候，我们并不是给整个轨迹 τ 都一样的分数，而是每一个状态-动作的对(pair)会分开来计算。(强化学习笔记：Policy-based Approach_UQI-LIUWJ的博客-CSDN博客4.2 小节）。

        实际上更新梯度的时候，如下式所示。 

        

         就是累积奖励减掉 bias，这一项就是估测出来的。

3.4  PPO的policy gradient

        我们通过重要性采样把 θ 变成 θ′。所以现在st​、at​ 是 θ′ 跟环境互动以后所采样到的数据。

         但是要调整参数是θ，又因为 θ′ 跟 θ 是不同的模型，所以你要做一个修正的项。这项修正的项，就是用重要性采样的技术，把 st​，at​ 用 θ 采样出来的概率除掉 st​、at​ 用 θ′ 采样出来的概率。

   于是我们得到下式：

         这边需要做一件事情是，假设模型是 θ 的时候，你看到st​ 的概率，跟模型是θ′ 的时候，你看到 st​ 的概率是差不多的，即 。因为它们是一样的，所以你可以把它删掉。

        于是我们得到下式：

        

          于是我们用 θ′ 去跟环境做互动，采样出 st​、at​ 以后，你要去计算 st​ 跟 at​ 的 advantage，然后你再去把它乘上。​ 是好算的，可以从这个采样的结果里面去估测出来的。在更新参数的时候，就是按照式(1) 来更新参数。

 3.4.1 为什么可以假设和 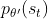是差不多的？

        因为你会看到什么状态往往跟你会采取什么样的动作是没有太大的关系的。比如说你玩不同的 Atari 的游戏，其实你看到的游戏画面都是差不多的，所以也许不同的 θ 对 st​ 是没有影响的。

        但更直觉的理由就是 很难算，想想看这项要怎么算，这一项说我有一个参数 θ，然后拿 θ 去跟环境做互动，算 st​ 出现的概率，这个你很难算。尤其如果输入是图片的话， 同样的st​ 根本就不会出现第二次。你根本没有办法估这一项， 所以干脆就无视这个问题。

        但是很好算。你手上有θ 这个参数，它就是个网络。你就把 st​ 带进去，（在Atari游戏的问题中，st​ 就是游戏画面），它就会告诉你某一个状态的 at​ 概率是多少。

       所以这一项，你只要知道θ 和θ′ 的参数就可以算。

3.3.5 PPO

                注意，由于在 PPO 中θ′ 是（上一轮更新的θ），所以 PPO 是 on-policy 的算法。

         重要性采样有一个问题：如果 跟这两个分布差太多的话，重要性采样的结果就会不好。怎么避免它差太多呢？这个就是 Proximal Policy Optimization (PPO)  在做的事情。

        我们在训练的时候，多加一个约束(constrain)【类似于正则项】。这个约束是 θ 跟θ′ 输出的动作的 KL 散度(KL divergence)，简单来说，这一项的意思就是要衡量说θ 跟θ′ 有多像。

        这里为什么是减号，我们这样想：在线性回归问题中，我们通过梯度下降的方法，减少损失函数（所以损失函数的系数是正的），同时减少各参数的大小（所以正则项的系数也是正的）。在这里通过梯度上升的方法，增加奖励（所以J的系数是正的），减少KL散度，所以KL散度的系数是负的

3.3.6 信任区域策略优化(Trust Region Policy Optimization，TRPO)

        PPO 有一个前身叫做信任区域策略优化(Trust Region Policy Optimization，TRPO)，TRPO 的式子如下式所示：

        

         它与 PPO 不一样的地方是约束摆的位置不一样，PPO 是直接把约束放到你要优化的那个式子里面，然后你就可以用梯度上升的方法去最大化这个式子。

        但 TRPO 是把 KL 散度当作约束，它希望 θ 跟θ′ 的 KL 散度小于一个 δ。如果你使用的是基于梯度的优化时，这个约束是很难处理的。

        TRPO 是很难处理的，因为它把 KL 散度约束当做一个额外的约束，没有放目标函数里面，所以它很难算，所以一般就用 PPO 而不是 TRPO。

       一般的文献上，PPO 跟 TRPO 性能差不多，但 PPO 在实现上比 TRPO 容易的多。

3.3.7    PPO的KL散度       

        公式里虽然是是直接把 KL 散度当做一个函数，输入是 θ 跟θ′，但并不是说把θ 或 θ′ 当做一个分布，算这两个分布之间的距离。

        所谓的θ 跟 θ′ 的距离并不是参数上的距离，而是行为(behavior)上的距离。

       行为上的距离是指，你先代进去一个状态 s，它会对这个动作的空间输出一个分布。假设你有 3 个动作，3 个可能的动作就输出 3 个值。行为距离就是说，给定同样的状态，输出动作之间的差距。这两个θ对应动作的分布都是概率分布，所以就可以计算这两个概率分布的 KL 散度。把不同的状态输出的这两个分布的 KL 散度平均起来才是我这边所指的两个 actor （Θ）间的 KL 散度。

3.3.8 为什么不直接算 θ 和θ′ 之间的距离？

        在做强化学习的时候，之所以我们考虑的不是参数上的距离，而是动作上的距离，是因为很有可能对 actor 来说，参数的变化跟动作的变化不一定是完全一致的。

        有时候你参数小小变了一下，它可能输出的行为就差很多。或者是参数变很多，但输出的行为可能没什么改变。

        所以我们真正在意的是这个 actor 的行为上的差距，而不是它们参数上的差距。

        所以在做 PPO 的时候，所谓的 KL 散度并不是参数的距离，而是动作的距离。

3.3.9 adaptive KL penalty

         在设计J的时候，有一个问题就是β 要设多少。adaptive KL penalty 中使用了一个动态调整 β 的方法。

• 在这个方法里面，你先设一个你可以接受的 KL 散度的最大值。假设优化完这个式子以后，你发现 KL 散度的项太大，那就代表说后面这个惩罚的项没有发挥作用，那就把 β 调大。（θ和θ'差距过大——>目标函数的作用是为了减少θ和θ’的差距——>增大β)
• 另外，你设一个 KL 散度的最小值。如果优化完上面这个式子以后，你发现 KL 散度比最小值还要小，那代表后面这一项的效果太强了，你怕他只弄后面这一项，那 θ 跟 θ‘ 都一样，这不是你要的，所以你要减少 β。（θ和θ'差距过小——>目标函数的作用是为了增大θ和θ’的差距——>减少β)

3.3.10 PPO-clip

        算 KL 散度很复杂，于是就有了PPO-clip。

        PPO-clip要去最大化的目标函数如下式所示，它的式子里面就没有 KL 散度 。

        

        这里clip函数是截取的意思，第一个参数小于第二个参数的时候，返回第二个参数；大于第三个参数的时候，返回第三个参数；否则返回第一个参数 

        

 

        虽然这个式子看起来有点复杂，实现起来是蛮简单的，因为这个式子想要做的事情就是希望跟，在优化以后不要差距太大。

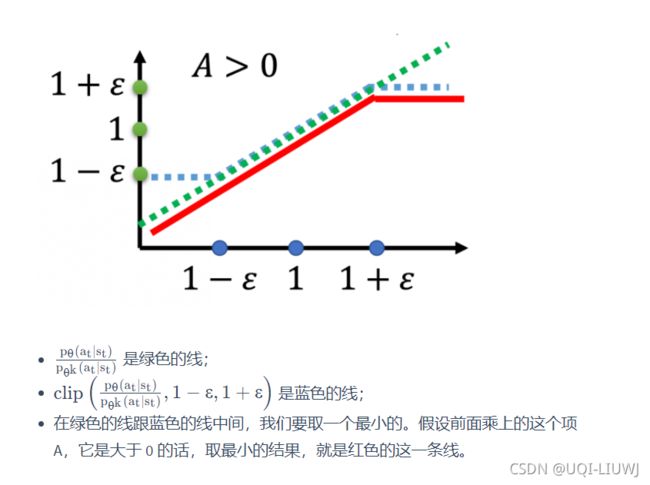
        如果 A > 0，也就是某一个状态-动作的对是好的，那我们希望增加这个状态-动作对的概率。也就是说，我们想要让越大越好，但它跟 的比值不可以超过 1+ε。

        如果 A < 0，也就是某一个状态-动作对是不好的，我们希望把减小。压到是 1−ϵ 的时候就停了，就不要再压得更小。

        这样的好处就是，你不会让 跟差距太大。

参考资料：第五章 近端策略优化 (PPO) 算法 (datawhalechina.github.io)