强化学习RL学习笔记9-近端策略优化算法（Proximal Policy Optimization, PPO）

强化学习笔记专栏传送

上一篇：强化学习RL学习笔记8-策略梯度（Policy Gradient）
下一篇：持续创作中…

前言

强化学习（Reinforcement Learning, RL），又称再励学习、评价学习或增强学习，是机器学习的范式和方法论之一，用于描述和解决智能体（agent）在与环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题 。

本文是笔者对强化学习的一点学习记录，成文于笔者刚开始接触强化学习期间，主要内容参考LeeDeepRL-Notes，学习期间很多概念和理论框架还很不成熟，若文中存在错误欢迎批评指正，也欢迎广大学习者沟通交流、共同进步。

---

From On-policy to Off-policy

• 如果要学习的 agent 跟和环境互动的 agent 是同一个， 叫做on-policy(同策略)。
• 如果要学习的 agent 跟和环境互动的 agent 不是同一个， 叫做off-policy(异策略)。

Policy gradient 是 on-policy 的做法，因为在做 policy gradient 时， agent 先去跟环境互动搜集资料，搜集很多的 $\tau$，根据搜集到的资料，会按照 policy gradient 的式子去更新 policy 的参数从而优化 agent 。所以 policy gradient 是一个 on-policy 的算法。

近端策略优化(Proximal Policy Optimization，简称 PPO) 是 policy gradient 的一个变形，是现在 OpenAI 默认的强化学习算法。

$$\nabla {\bar{R}}_{\theta }=E_{\tau \sim p_{\theta }(\tau )}\left[R(\tau )\nabla \log p_{\theta }(\tau )\right]$$

直接使用上式更新梯度的 policy gradient 问题在于每次 sample 的轨迹用于更新一次 policy 之后，$\theta$ 发生改变，sample 的轨迹便不能再被使用，需要重新 sample 进一步更新 policy。这是 on-policy 的弊端。

而若使用 off-policy 的策略，用 θ′ 跟环境做互动。用 θ′ 收集到的数据去训练 θ。这意味着可以把 θ′ 收集到的数据用非常多次，可以使用同样的 sample 执行梯度上升 (gradient ascent) 数次，这样会提升执行的效率。

Importance Sampling

概念

具体使用 off-policy 的方法是 importance sampling(重要性采样)。

假设有一个函数 $f(x)$，要计算从 p 这个分布采样 x，再把 x 带到 f 里面，得到 $f(x)$。可以从 p 这个分布去采样一些数据 $x^i$ 。把 $x^i$ 代到 $f(x)$ 里面，然后取平均值，就可以近似 $f(x)$ 的期望值。如下式所示：

$$E_{x\sim p}[f(x)]\approx \frac{1}{N}\sum _{i=1}^{N}f(x^i)$$

因为现在要做 off-policy ，采样的所以做一个修正，修正是这样的。期望值 $E_{x\sim p}[f(x)]$ 其实就是 $\int f(x)p(x)dx$ ，对其做如下的变换：

$$\int f(x)p(x)dx=\int f(x)\frac{p(x)}{q(x)}q(x)dx=E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]$$

即可以在 $q(x)$ 分布下采样数据，根据上式通过计算 $f(x)\frac{p(x)}{q(x)}$ 的期望从而得到 $E_{x\sim p}[f(x)]$。

重要性采样有一些问题。虽然理论上可以把 p 换成任何的 q。但是在实现上， p 和 q 不能差太多。差太多会有一些问题。

$$E_{x\sim p}[f(x)]=E_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]$$

虽然上式成立，但两个随机变量的期望一样，并不代表方差一样。也就是说，只要对 p 这个分布采样够多次，q 这个分布采样够多，得到的结果会是一样的。但是如果采样的次数不够多，因为它们的方差差距是很大的，所以就有可能得到非常大的差别。

举个例子，当 p(x) 和 q(x) 差距很大的时候，会发生什么样的问题。

假设蓝线是 $p(x)$ 的分布，绿线是 $q(x)$ 的分布，红线是 $f(x)$ 。

如果我们要计算 $f(x)$ 的期望值，从 $p(x)$ 这个分布做采样的话，那显然 $E_{x\sim p}[f(x)]$ 是负的，因为左边那块区域 $p(x)$ 的概率很高，所以大部分采样都会采样到这个地方，而 $f(x)$ 在这个区域是负的， 所以理论上这一项算出来会是负。

同理，若在 $q(x)$ 采样，少量采样时得到的 $f(x)$ 值都会是正的，若某次采样到概率较小的左侧区域还是有机会使 $E_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]$ 变负，但采样较少的情况下会出现 $E_{x\sim p}[f(x)]$ 为负，$E_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]$ 为正的不合理情况。

应用重要性采样

通过使用重要性采样，可以将 on-policy 训练的算法改为 off-policy 的情况。

之前我们是拿 $\theta$ 这个 policy 去跟环境做互动，采样出轨迹 $\tau$，然后计算 $R(\tau )\nabla \log p_{\theta }(\tau )$ 。现在我们不用 $\theta$ 去跟环境做互动，假设有另外一个 policy ${\theta }^{\prime }$，我们现在的 $\tau$ 是从 ${\theta }^{\prime }$ 采样出来的，是拿 ${\theta }^{\prime }$ 去跟环境做互动，要补上一个重要性权重 $\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}$ 。这个重要性权重就是某一个轨迹 $\tau$ 用 $\theta$ 算出来的概率除以这个轨迹 $\tau$ 用 ${\theta }^{\prime }$ 算出来的概率。

off-policy 的好处在于θ 可以更新参数很多次，一直到 $\theta$ 训练到一定的程度，更新很多次以后，${\theta }^{\prime }$ 再重新去做采样。

如上篇博客所说，实际在做 policy gradient 的时候，并不是给整个轨迹 $\tau$ 一样的分数，而是每一个状态-动作的对会分开来计算。实际上更新 gradient 的时候，如下式所示：

$$\nabla {\bar{R}}_{\theta }\approx E_{\left(s_t,a_t\right)\sim {\pi }_{\theta }}\left[A^{\theta }\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]$$

其中 $A^{\theta }\left(s_t,a_t\right)$ 是累积奖励的值减掉 baseline，即：

$$A^{\theta }\left(s_t,a_t\right)=\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n-b$$

现在用了重要性采样的技术把 on-policy 变成 off-policy，就从 $\theta$ 变成 ${\theta }^{\prime }$ 。所以现在 $s_t$、$a_t$ 是 ${\theta }^{\prime }$ 即另一个 actor 跟环境互动以后所采样到的数据。 但是拿来训练要调整参数是模型 $\theta$。因为 ${\theta }^{\prime }$ 跟 $\theta$ 是不同的模型，所以需要修正项。这项修正项，就是用重要性采样的技术，把 $s_t$、$a_t$ 用 $\theta$ 采样出来的概率除掉 $s_t$、$a_t$ 用 ${\theta }^{\prime }$ 采样出来的概率。

$$E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{P_{\theta }\left(s_t,a_t\right)}{P_{{\theta }^{\prime }}\left(s_t,a_t\right)}{A}^{\theta }\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]$$

拆解 $p_{\theta }\left(s_t,a_t\right)$ 和 $p_{{\theta }^{\prime }}\left(s_t,a_t\right)$ 即

$$\begin{array}{rl}{p}_{\theta }\left(s_t,a_t\right)& =p_{\theta }\left(a_t|s_t\right)p_{\theta }(s_t)\\ p_{{\theta }^{\prime }}\left(s_t,a_t\right)& =p_{{\theta }^{\prime }}\left(a_t|s_t\right)p_{{\theta }^{\prime }}(s_t)\end{array}$$

​

于是得到下式：

$$E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}\frac{p_{\theta }\left(s_t\right)}{p_{{\theta }^{\prime }}\left(s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]$$

假设模型 $\theta$ 时看到 $s_t$ 的概率，和模型 ${\theta }^{\prime }$ 的时候看到 $s_t$ 的概率是差不多的，即 $p_{\theta }(s_t)=p_{{\theta }^{\prime }}(s_t)$ 因为它们是一样的，所以可以把这一项比值删掉，即

$$E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]\text{\hspace{1em}(1)}$$

上述假设成立的原因是会看到什么状态往往和会采取什么样的动作是没有太大关系的，而且 $s_t$ 出现的概率很难算，所以忽略这个问题。

现在得到一个新的目标函数：

$$J^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right]$$

当使用重要性采样的时候，要优化的目标函数就是这样，把它写作 $J^{{\theta }^{\prime }}(\theta )$。这个括号里 $\theta$ 代表要优化的参数。${\theta }^{\prime }$ 是说拿 ${\theta }^{\prime }$ 做示范，即真正在跟环境互动的是 ${\theta }^{\prime }$ 。因为 $\theta$ 不跟环境做互动，是 ${\theta }^{\prime }$ 在跟环境互动。

实际上在更新参数的时候，就是按照式(1) 来更新参数。

---

PPO

在 off-policy 的方法里要优化的是 $J^{{\theta }^{\prime }}(\theta )$ ，但是这个目标函数又牵涉到重要性采样。在做重要性采样时，$p_{\theta }\left(a_t|s_t\right)$ 不能跟 $p_{{\theta }^{\prime }}\left(a_t|s_t\right)$ 差太多。所以在训练的时候，多加一个约束(constrain)。这个约束是 $\theta$ 跟 ${\theta }^{\prime }$ 输出的动作的 KL 散度(KL divergence)，简单来说，这一项就是要衡量 $\theta$ 跟 ${\theta }^{\prime }$ 有多像。

下式即 Proximal Policy Optimization (PPO) 公式：
$$J^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right]$$

$$J_{PPO}^{{\theta }^{\prime }}(\theta )=J^{{\theta }^{\prime }}(\theta )-\beta KL(\theta ,{\theta }^{\prime })$$

PPO 有一个前身叫做信任区域策略优化(Trust Region Policy Optimization，TRPO)，TRPO 的式子如下式所示。

$$\begin{array}{r}{J}_{TRPO}^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right]\\ \\ \mathrm{K}\mathrm{L}\left(\theta ,{\theta }^{\prime }\right)<\delta \end{array}$$

TRPO 与 PPO 不一样的地方是约束的位置不一样，PPO是直接把约束放到要优化的式中，然后就可以用梯度上升的方法最大化该式。但 TRPO 是把 KL 散度当作约束，它希望 $\theta$ 跟 ${\theta }^{\prime }$ 的 KL 散度小于 $\delta$。如果使用的是基于梯度的优化时，有约束是很难处理的，所以 PPO 在实现上比 TRPO 容易的多。

==所谓的 KL 散度并不是参数的距离，而是动作的距离。==假设有一个模型，有一个 actor 是 $\theta$，另外一个 actor 的参数是 ${\theta }^{\prime }$ ，所谓参数上的距离就是这两组参数有多像。行为距离就是给定同样的状态时输出动作之间的差距。

PPO-Penalty

PPO 算法有两个主要的变种：PPO-Penalty 和 PPO-Clip。

首先是 PPO1 的算法，即 PPO-Penalty。

先初始化一个 policy 的参数 ${\theta }^0$。然后在每一个迭代中，用参数 ${\theta }^k$ ，${\theta }^k$ 就是在前一个训练的迭代得到的 actor 的参数，用 ${\theta }^k$ 跟环境做互动，采样到一大堆状态-动作的对。采样到这组数据以后，可以让 $\theta$ 更新很多次，想办法去最大化目标函数。
$$J_{PPO}^{{\theta }^{\prime }}(\theta )=J^{{\theta }^{\prime }}(\theta )-\beta KL(\theta ,{\theta }^{\prime })$$

上式中 $\beta$ 要设成多少，这里介绍一个动态调整 $\beta$ 的方法：adaptive KL divergence

• 先设一个 KL 散度可以接受的最大值。然后优化完后，KL 散度的项大于最大值，那就代表后面惩罚的项没有发挥作用，就把 $\beta$ 调大。
• 另外定一个 KL 散度最小值。如果优化完后，KL 散度比最小值还要小，那代表后面一项的效果太强，此时减小 $\beta$。

PPO-Clip

如果觉得算 KL 散度 很复杂，有 PPO2，PPO2 即 PPO-Clip。PPO2 要去最大化的目标函数如下式所示，式子里没有 KL 散度 。

$$\begin{array}{rl}{J}_{PPO2}^{{\theta }^k}(\theta )\approx \sum _{\left(s_t,a_t\right)}\min & \left(\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}{A}^{{\theta }^k}\left(s_t,a_t\right),\mathrm{clip}\left(\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)},1-\epsilon ,1+\epsilon \right)A^{{\theta }^k}\left(s_t,a_t\right)\right)\end{array}$$

• 第二项前面有 clip 函数，clip 函数的意思是，在括号里有 3 项，如果第一项小于第二项的话，那就输出 $1-\epsilon$ 。第一项如果大于第三项的话，那就输出 $1+\epsilon$。简言之就是第一项如果在第二项和第三项形成的区间内，就输出第一项，否则小于第二项时输出第二项，大于第三项时输出第三项。
• $\epsilon$ 是一个超参数，可以设成 0.1 或 0.2 。

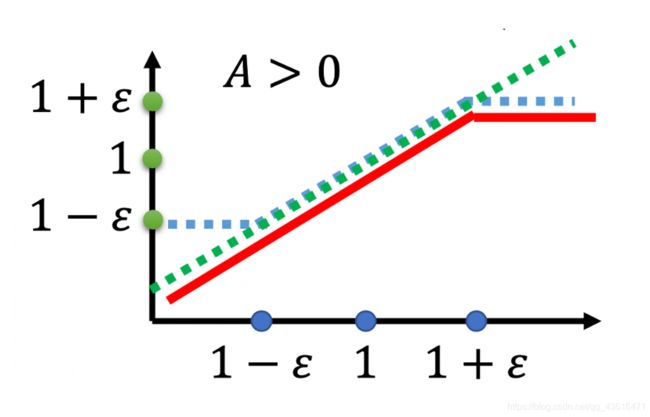
上图的横轴是 $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}$ ，纵轴是 clip 函数的输出。

• 如果 $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}$ 大于$1+\epsilon$，输出就是 $1+\epsilon$。

• 如果小于 $1-\epsilon$， 它输出就是 $1-\epsilon$。

• 如果介于 $1+\epsilon$ 跟 $1-\epsilon$ 之间， 就是输入等于输出。
  ​
  

• $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}$ 是绿色的线；

• $\mathrm{clip}\left(\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)},1-\epsilon ,1+\epsilon \right)$ 是蓝色的线；

• 在绿色的线跟蓝色的线中间，要取一个最小的。假设两项前面乘的项 A是大于 0 的话，取最小的结果，就是红色的这一条线。

若 A 小于 0 ，取较小的后，就得到红色的这一条线。

这个式子想做的事就是使 $p_{\theta }(a_t|s_t)$ 跟 $p_{{\theta }^k}(a_t|s_t)$ 在优化后差距不要太大，也就是你拿来做示范的模型跟你实际上学习的模型在优化以后不要差距太大。

• 如果 A > 0，也就是某一个状态-动作对是好的，那我们希望增加这个状态-动作对的概率。也就是说，我们想让 $p_{\theta }(a_t|s_t)$ 越大越好，但它跟 $p_{{\theta }^k}(a_t|s_t)$ 的比值不可以超过 $1+\epsilon$。如果超过 $1+\epsilon$ ，就没有 benefit 了。红色的线就是我们的目标函数，我们希望目标越大越好，我们希望 $p_{\theta }(a_t|s_t)$ 越大越好。但是 $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}$ 只要大过 $1+\epsilon$，就没有 benefit 了。所以在训练的时候，当 $p_{\theta }(a_t|s_t)$ 被训练到 $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}>1+\epsilon$ 时，它就会停止。假设 $p_{\theta }(a_t|s_t)$ 比 $p_{{\theta }^k}(a_t|s_t)$ 还要小，并且这个 advantage 是正的。因为这个动作是好的，当然希望这个动作被采取的概率越大越好，即希望 $p_{\theta }(a_t|s_t)$ 越大越好。所以假设 $p_{\theta }(a_t|s_t)$ 还比 $p_{{\theta }^k}(a_t|s_t)$ 小，那就尽量把它挪大，但只要大到 $1+\epsilon$ 就好。

• 如果 A < 0，也就是某一个状态-动作对是不好的，我们希望把 $p_{\theta }(a_t|s_t)$ 减小。如果 $p_{\theta }(a_t|s_t)$ 比 $p_{{\theta }^k}(a_t|s_t)$ 还大，那你就尽量把它压小，压到 $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}$ 是 $1-ϵ$ 的时候就停了，就不要再压得更小。

这样的好处就是，你不会让 $p_{\theta }(a_t|s_t)$ 跟 $p_{{\theta }^k}(a_t|s_t)$ 差距太大。

---

上一篇：强化学习RL学习笔记8-策略梯度（Policy Gradient）
下一篇：持续创作中…