搞定动态规划----一篇足矣

---

前言

最近一周在做二叉树的相关题目，发现大部分能用递归解决的题目都可以用动态规划搞定，所以今天分享一下动态规划的相关知识和解题套路。

---

本人才疏学浅，若有不足和错误，请联系我进行补充和更改。

一、动态规划

1.算法解析

动态规划是一种分治思想，但与分治算法不同之处在于，分治算法是把原问题分解为若干的子问题，自顶向下求解各子问题，然后对各子问题的解进行合并，求出原问题的解。而动态规划则是原问题分成若干子问题后，自底而上，先求解最小的子问题，然后依靠最小子问题的解来得出次小子问题的解，直至解出原问题的解。

2.算法要素

问题是否适合动态规划，需分析问题是否具有以下性质：

- 最优子结构
最优子结构指问题的最优解是由其子问题的最优解构建而成。如果不具备最优子结构性质，那么就不能使用动态规划来解决。

- 子问题重叠

问题重叠是指在求解子问题的过程中有大量子问题是重复的，那么只需要求解一次，将结果存储到表中，以后再使用时就可以直接查询，不用重新计算。子问题重叠不是运用动态规划的必要条件，但是动态规划的优势体现。

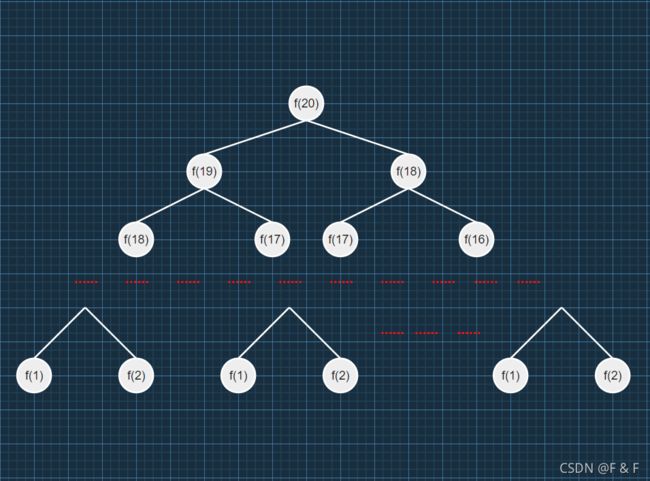
我以求斐波拉契数列的前 20 项值为例，来说明一下子问题重叠：
下图中的 f(18) 在求 f(19) 和 f(20) 时都会用到，所以我们只需要在求解 f(19)时记录求出的 f(18) 的解即可。

3.思考步骤

看到问题时，可以按照以下思路进行考虑：

• 分析最优解的结构特征
• 建立最优值的递归式
• 自底而上计算最优值，并记录
• 构造最优解

二、案例分析 1 ----最长公共子序列

1、问题描述

给定两个序列 X={x1 , x2 , x3 , x4 ,······, xm } 和 Y={y1 , y2 , y3 , y4 ,······, yn } ，找出 X 和 Y 的一个最长公共子序列。例如 X= { A ,B ,C ,B ,D} , Y ={ B ,C ,B ,D },那么 X 和 Y 的最长公共子序列是 B ,C ,B ,D 。

2、问题分析

按照我们上面的思路进行分析：

- 最优解的结构特征
首先进行假设：假设Zk={ z1 , z2 , z3 ,····· , zk }是Xm={ x1 , x2 , x3 ,····· , xm}和Yn={ y1 ,y2 ,y3 ,······ , yn}的最长公共子序列。那么，我们就可以有以下三种情况的讨论：

• 如果zk=xm=yn：那么就可以证明Z（k-1）是X（m-1）和Y（n-1）的最长公共子序列；
  

• 如果zk！=xm 且 yn！=xm：那么就可说明Zk是X（m-1）和 Yn的最长公共子序列；
  

• 如果zk!=yn 且 yn !=xm:那么就说明ZK 是Xm 和Y（n-1）的最长公共子序列；
  

- 最优值的递推式

设C[ i ][ j ]表示Xi 和Yj的最长公共子序列的长度。那么，我们就可以根据上面最优解的结构特征来分别得出每种情况下的递推式：

• xm=yn=zk：那么C[ i ][ j ]=C[ i-1 ][ j-1 ]+1 ;
• xm!=yn : 那么C[ i ][ j ]=MAX( C[i-1][ j ] , C[ i ][ j-1 ] ) ;

- 求解最优值

i =1 时：{ X1 }和{ Y1 ,Y2 ,Y3 ,······ ,Yn }中的字符逐一比较，按照递推式求解最长公共子序列长度。

i =2 时：{ X2 }和{ Y1 ,Y2 ,Y3,······, Yn }中的字符逐一比较，按照递推式求解最长公共子序列长度。

i =3时：{ X3 }和{ Y1 ,Y2 ,Y3,······，Yn }中的字符逐一比较，按照递推式求解最长公共子序列长度。

······

i =m时：{ Xm }和{ Y1 ,Y2 ,Y3 ,······, Yn }中的字符逐一比较，按照递推式求解最长公共子序列长度。

- 构造最优解

我们上面得到的C[ i ][ j ]仅仅可以知道两个字符串的最长公共子序列的长度，不能得出最长公共子序列是什么，所以，我们需要在每次比较的时候来记录一下当前要得出的这个值的来源是什么，是来自递推式中的哪一种情况。
例如：
假设我们现在求出了C[ m ][ n ]=5,表示Xm 和Yn的最长公共子序列的长度是5，但是这个5所代表的序列的得出可以采用反追踪，根据递推式，我们知道有如下几种情况：
Xi=Yi时：C[ i ][ j ]=C[ i-1 ][ j -1]+1;
Xi!=Yi时：C[ i ][ j ]=MAX( C[i-1][ j ],C[ i ][ j-1 ] )
我们可以用特定的数字或者符号去标记这三种情况，也就是在每次比较的时候都对每次的情况来源进行记录，我们可以假设：
C[ i ][ j ]=C[ i-1][ j-1]+1 对应 b[ i ][ j ]=1;
C[ i ][ j ]=C[ i ][ j-1] 对应 b[ i ][ j ]=2;
C[ i ][ j ]=C[ i-1][ j ]对应b[ i ][ j ]=3.
这样就可以根据b[ i ][ j ]数组进行反追踪。

3.步骤详述

假设求字符串S1=“ABCADAB” , S2="BACDBA"的最长公共子序列

1. 初始化

我们根据示例可以得出两个字符串的长度分别是L1=7，L2=6，所以我们创建一个C[ 7 ][ 8 ]的二维数组，为了方便起见，我们将数组的所有值都初始化为 0 .

2. 填充数组

i=1时：S1[ 0 ]与 S2[ j-1 ]比较，j=1 ，2 ，3，······，L2;
如果字符相等，C[ i ][ j ]取左上角数值加 1，，并记录b[ i ][ j ]=1;
如果字符不相等，取左侧和上面数值中的最大值，如果左侧和上面都相等，那么随便选一就行，并分别记录b[ i ][ j ]=2和b[ i ] [ j ]=3.

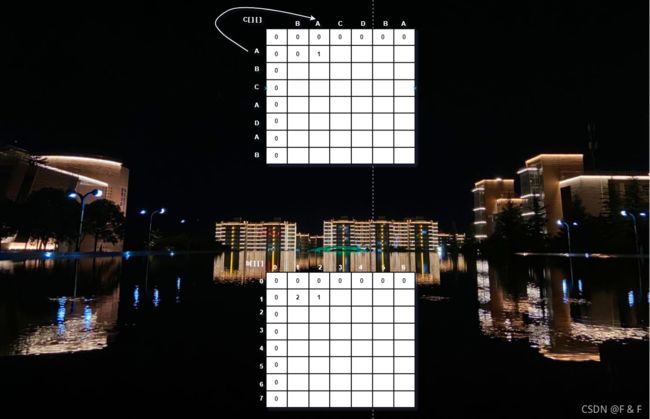
• j=1: A !=B,左侧等于上面，随机取数值，取左侧，得出C[ i ][ j ]=0,并记录最优来源b[ i ][ j ]=2：
  
• j=2：A=A ，则取左上角数值加1，可得C[ 1 ][ 2 ]=C[ 0 ][ 1 ]+1,最优决策来源b[ 1][ 2 ]=1：
  
• j=3：A !=C,左侧大于上面，取左值，C[ 1 ][ 3 ]=1,b[ 1 ][ 3 ]=2:
  
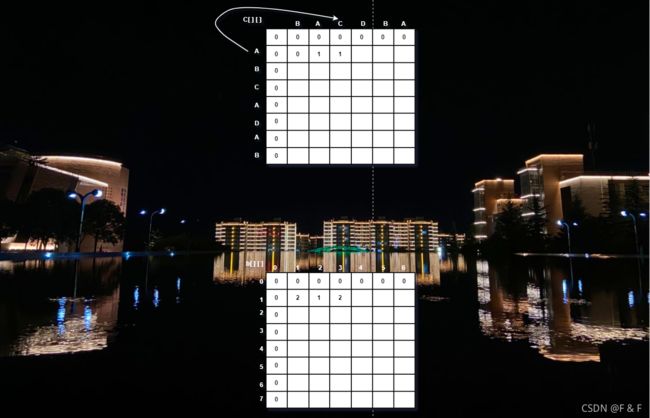
• j=4： A !=D，左侧大于上面，取左值，C[ 1 ][ 4 ]=1,b[ 1 ][ 4 ]=2:
  
• j=5：A !=B,左侧大于上面，取左值，C[ 1 ][ 5 ]=1,b[ 1 ][ 5 ]=2:
  
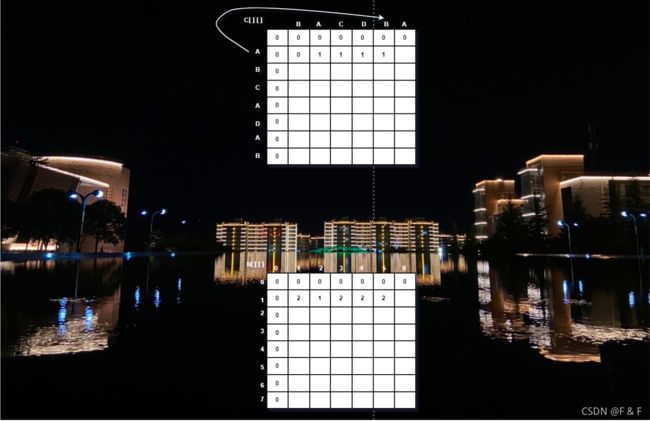
• j=6：A=A,取左上方值加1，C[ 1 ][ 6 ]=1,b[ 1 ][ 6 ]=1:
  
  - i=2时：
  S1[ 1 ]与 S2[ j-1 ]比较，j=1，2，3，······，L2，剩余情况和 i=1 时一样，数组C[ i ][ j ]和数组b[ i ][ j ]的取值方法都一样。这里我直接贴出结果：
  

剩余情况和上面的示例一样，只需要按照其方法继续进行即可，最终结果如下：

4.代码实现

Python代码：

def lcs(a, b):
    lena = len(a)
    lenb = len(b)
    c = [[0 for i in range(lenb + 1)] for j in range(lena + 1)]
    flag = [[0 for i in range(lenb + 1)] for j in range(lena + 1)]
    for i in range(lena+1):
        for j in range(lenb+1):
            if a[i] == b[j]:
                c[i + 1][j + 1] = c[i][j] + 1
                flag[i + 1][j + 1] = 'ok'
            elif c[i + 1][j] > c[i][j + 1]:
                c[i + 1][j + 1] = c[i + 1][j]
                flag[i + 1][j + 1] = 'left'
            else:
                c[i + 1][j + 1] = c[i][j + 1]
                flag[i + 1][j + 1] = 'up'
    return flag


def printLcs(flag, a, i, j):
    if i == 0 or j == 0:
        return
    if flag[i][j] == 'ok':
        printLcs(flag, a, i - 1, j - 1)
        print(a[i - 1], end='')
    elif flag[i][j] == 'left':
        printLcs(flag, a, i, j - 1)
    else:
        printLcs(flag, a, i - 1, j)


a = 'ABCBDAB'
b = 'BDCABA'
flag = lcs(a, b)
printLcs(flag, a, len(a), len(b))

C++代码：

void LCSL()
{
    int i,j;
    for(i=1;i<=len1;i++)
        for(j=1;j<=len2;j++)
        {
            if(s1[i-1]==s2[j-1])
            {
                c[i][j]=c[i-1][j-1]+1;
                b[i][j]=1;
            }
            else
            {
                if(c[i][j-1]>=c[i-1][j])
                {
                    c[i][j]=c[i][j-1];
                    b[i][j]=2;
                }
                else
                {
                c[i][j]=c[i-1][j];
                b[i][j]=3;
                }
            }
        }
}

C语言代码：文章摘自

#include
#include

int max(int a,int b)
{
   return a>b?a:b;
}
int main()
{
    int i,j,k;
    char a[600];
    char b[600];
    int f[600][600];
    while(scanf("%s %s",a,b)!=EOF)
    {
        int n=strlen(a);
        int m=strlen(b);
        for(i=0;i<=n;i++)
        {
            f[i][0]=0;
        }
        for(i=0;i<=m;i++)
        {
            f[0][i]=0;
        }
        for(i=1;i<=n;i++)
        {
            for(j=1;j<=m;j++)
            {
                if(a[i-1]==b[j-1])
                {
                    f[i][j]=f[i-1][j-1]+1;
                }
                else
                {
                    f[i][j]=max(f[i-1][j],f[i][j-1]);
                }
            }
        }
        printf("%d\n",f[n][m]);
    }
    return 0;
}

Java代码：文章摘自

package dp;

import java.util.Random;

//使用动态规划找出最长公共子序列
public class LCS {
    public static void main(String[] args) {
        //随机生成指定长度的字符串
        int size = 20;
        String x  = generateRandomStr(size);
        String y  = generateRandomStr(size);

        int m = x.length();
        int n = y.length();
        //创建二维数组，也就是填表的过程
        int[][] c = new int[m+1][n+1];

        //初始化二维数组
        for (int i = 0; i < m+1; i++) {
            c[i][0] = 0;
        }
        for (int i = 0; i < n+1; i++) {
            c[0][i] = 0;
        }

        //实现公式逻辑
        int[][] path = new int[m+1][n+1];//记录通过哪个子问题解决的，也就是递推的路径
        for (int i = 1; i < m+1; i++) {
            for (int j = 1; j < n+1; j++) {
                if(x.charAt(i-1) == y.charAt(j-1)){
                    c[i][j] = c[i-1][j-1] + 1;
                }else if(c[i-1][j] >= c[i][j-1]){
                    c[i][j] = c[i-1][j];
                    path[i][j] = 1;
                }else{
                    c[i][j] = c[i][j-1];
                    path[i][j] = -1;
                }
            }
        }
        //输出查看c
        System.out.println("c:");
        for (int i = 0; i < m+1; i++) {
            for (int j = 0; j < n+1; j++) {
                System.out.print(c[i][j]+"\t");
            }
            System.out.println();
        }
        //输出查看path
        System.out.println("path:");
        for (int i = 0; i < m+1; i++) {
            for (int j = 0; j < n+1; j++) {
                System.out.print(path[i][j]+"\t");
            }
            System.out.println();
        }

        System.out.printf("%s与%s的最长公共子序列为：\n",x,y);
        PrintLCS(path,x,m,n);


    }

    public static String generateRandomStr(int length) {
        String base = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
        Random random = new Random();
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < length; i++) {
            int number = random.nextInt(base.length());
            sb.append(base.charAt(number));
        }
        return sb.toString();
    }
    public static void PrintLCS(int[][]b,String x,int i,int j){
        if(i == 0 || j == 0){
            return;
        }

        if(b[i][j] == 0){
            PrintLCS(b,x,i-1,j-1);
            System.out.printf("%c",x.charAt(i-1));
        }else if(b[i][j] == 1){
            PrintLCS(b,x,i-1,j);
        }else{
            PrintLCS(b,x,i,j-1);
        }
    }
}

三、案例分析 2 ----最优三角剖分

1、问题描述

有一块多边形的披萨饼，上面有很多蔬菜和肉片，我们希望沿着不相邻的顶点切成小三角形，并且尽可能少的切碎披萨上面的肉片和蔬菜。

2、问题分析

可以将披萨看作一个凸多边形，最优三角划分指各三角形上权值之和最小。

- 最优子结构性质
假设知道从第 k 个点切开会得到最优解，那么原问题就变成三部分，分别是：{ V0，V1，······, Vk } 和 { Vk，Vk+1，······，Vn } 和 三角形V0VkVn。

• 假设{ v0,v1,v2,······vn}的三角剖分权值之和为c，{ v0,v1,v2,······,vk }的权值之和为a，{ vk,vk+1,······，vn }的权值之和为b，三角形v0 vk vn 的值为w，那么c=a+b+w
• 最优递归式：
  m[ i ] [ j ]=min(m[ i ][ k ]+m[ k+1][ j ]+w), i

3.步骤叙述

顶点数n，依次输入各个顶点之间的连接权值存储在邻接矩阵g[ i ][ j ]中。

该题和上一题思路基本一致，暂不做陈述，若有疑问，可以私信或评论找我拿取详细解题思路与图解。

4.代码实现

Python代码：

"""二维数组g记录各个顶点之间的连接权值，二维数组m存放各个子问题的最优值，二维数组s存放最优决策"""
def convexpolygontriangulation(g):
    m=[[0]*len(g)]*len(g)
    s=m
    for a in range(2,len(g+1)):
        for i in range(1,len(g)-a+1):
            j=i+a-1
            for k in range(i+1,j):
                temp=m[i][k]+m[k-1][j]+g[i-1][k]+g[k][j]+g[i-1][j]
                if m[i][j]>temp:
                    m[i][j]=temp
                    s[i][j]=k
    print(m)

g=[
    [0,2,3,1,5,6],
    [2,0,3,4,8,6],
    [3,3,0,10,13,7],
    [1,4,10,0,12,5],
    [5,8,13,12,0,3],
    [6,6,7,5,3,0]
    ]
convexpolygontriangulation(g)

C语言代码：文章转自

#include

using namespace std;


 int w[6][6] = { { 0,2,2,3,1,4 },
                { 2,0,1,5,2,3 },
                { 2,1,0,2,1,4 },
                { 3,5,2,0,6,2 },
                { 1,2,1,6,0,1 },
                { 4,3,4,2,1,0 } };

 int d[10][10];

 int weight(int i,int j,int k){
    
    return w[i][j]+w[j][k]+w[i][k];
    
}


int main(){
    int n=6;    
    
  
   memset(d,0x3f,sizeof(d));
 
    
    for(int i=0;i<n;i++)
    d[i][(i+1)%n]=0,d[i][i]=0;
    
    for(int len=2;len<n;len++)
    for(int i=0;i<n-len;i++){                                  //从0点开始，一直到n-len-1，都可以作为起点构造长度为len的多边形；
        int k=i+len;
        for(int j=i+1;j<k;j++)                                 
        d[i][k]=min(d[i][k],d[i][j]+d[j][k]+weight(i,j,k));
            
    }    
    
    printf("%d",d[0][5]);
}

C++代码：

#include
#include
using namespace std;
 
//坐标转化为权值，将权值储存在图的矩阵表示weight[][]中，然后利用课本上的 MinweightTriangulation函数 
int weight[500][500];
//计算权值，即边长 
int Sum(int x1, int x2, int y1, int y2)
{
	int p, q;
	p = pow(x1-y1,2) + pow(x2-y2,2);
	q = sqrt(p);
	return q;
}
//交换函数 
void Exchange(int a[500][2],int flag)
{
	int temp;
	temp = a[0][0];
	a[0][0] = a[flag][0];
	a[flag][0] = temp;
	
	temp = a[0][1];
	a[0][1] = a[flag][1];
	a[flag][1] = temp;
}
//返回权值和 
int Weight(int a,int b,int c)
{
	return weight[a][b] + weight[a][c] + weight[b][c];
}
//计算最优值 
void MinweightTriangulation(int n,int m[500][500],int s[500][500])
{
	for(int i = 1;i <= n; i++)
		m[i][i]=0;
	for(int r = 2;r <= n; r++)
		for(int i = 1;i <= n-r+1; i++) 
		{
			int j = i+r-1;
			m[i][j] = m[i][i] + m[i+1][j] + Weight(i-1,i,j);
			s[i][j] = i;
			for(int k = i+1;k < j; k++)
			{
				int t = m[i][k] + m[k+1][j] + Weight(i-1,k,j);
				if(t < m[i][j])
				{
					m[i][j] = t;
					s[i][j] = k;
				}
			}
		} 
 } 
//构造最优解 
void Traceback(int i,int j,int s[500][500])
{
	if(i == j)
		return;
	Traceback(i, s[i][j], s);
	Traceback(s[i][j]+1, j, s);
	cout << i-1 << s[i][j] << j << endl;
}

int main()
 {
 	//a[][]存坐标，t[][]最优权值，s[][]第3个顶点位置 
 	int a[500][2], t[500][500], s[500][500];
 	int n, flag = 0;
 	cin >> n;
 	for(int i=0;i < n; i++)
 	{
 		for(int j = 0;j < 2; j++)
 		cin >> a[i][j];
	 }
	 for(int i = 0;i < n; i++)
	 {
	 	for(int j = 0;j < n;j++)
	 	{
	 		weight[i][j] = Sum(a[0][0],a[0][1],a[j][0],a[j][1]);
		}
		flag = i + 1;
		if( flag < n){
			Exchange(a, flag);
		} 
	}
	
	MinweightTriangulation(flag-1, t, s);
	Traceback(1, flag-1, s); 
 }

总结

如果大家对本文的动态规划有何疑问或者建议，可以联系本人进行商讨。本人才疏学浅，错误在所难免，还望各位多多指正与包涵。

致谢

感谢陈小玉教授的指导；
感谢京东的大哥百忙之中的辅导与支持；
感谢致易工作室的学长和小伙伴们的支持与帮助；
感谢我家莫莫的陪伴，你又何尝不是我的一片蓝天。