[人工智能-深度学习-9]:神经网络基础 - 常见loss损失函数之均分误差MSE、绝对值误差MAE、平滑平均绝对误差Huber
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120478132
目录
第1章 什么损失函数
1.1 什么是机器学习
1.2 什么是监督式机器学习
1.3 什么是损失函数
第2章 平均绝对误差损失Mean Absolute Error Loss(MAE)
2.1 概述
2.2 loss函数的数学表达式
2.3 loss函数的几何图形与意义
2.4 特点
第3章 均方差损失 Mean Squared Error Loss(MSE)
3.1 概述
3.2 loss函数的数学表达式
3.3 loss函数的几何图形与意义
3.4 特点
第4章 MSE与MAE的比较
第5章 平滑平均绝对误差Huber Loss (SMAE)
5.1 概述
5.2 SMAE的loss函数的数学表达式 - 方法1
5.2 SMAE的loss函数的数学表达式 - 方法2
5.3 特点
第1章 什么损失函数
1.1 什么是机器学习
![]()
[人工智能-深度学习-8]:神经网络基础 - 机器学习、深度学习模型、模型训练_文火冰糖(王文兵)的博客-CSDN博客
1.2 什么是监督式机器学习
![]()
百度百科:监督式学习(英语:Supervised learning),是一个机器学习中的方法,可以由训练资料中学到或建立一个模式(函数 / learning model),并依此模式推测新的实例。
训练资料是由输入物件(通常是向量)和预期输出所组成。
函数的输出可以是一个连续的值(称为回归分析),或是预测一个分类标签(称作分类)。
白话:所谓监督室式学习,给定的数据集和对应的标准答案,即标签。让机器以后的数据集合标准答案进行学习。
其中,数据集用{Xi}表示,对应的标签值,又称为样本值,期望值,用{Yi} 表示。
神经网络模型,利用当前的参数,对对数据集{Xi}进行运算和预测,获得的输出值为{Yi_pred}.
也就是说,监督室学习,是指有标准答案的学习。
标准答案的形式:
- 标签值
- 样本值
备注:标签值、样本值、期望值,并不是没有任何错误的值期望值,而是人为的采样值,是表面现象下参考值,并不一定是内涵的规律值。
1.3 什么是损失函数
监督学习本质上是给定一系列训练样本 {Xi},尝试学习样本的映射关系 {Xi -> Yi},使得给定一个 x_real,即便这个 x_real不在训练样本{Xi -> Yi}中,也能够得到其输出值{Y_pred}尽量接近真实{Y_real}的输出。
损失函数(Loss Function)则是这个过程中关键的一个组成部分,用来衡量模型的预测输出{Y_pred}与样本真实值{Yi}的之间的差距,并给模型的优化指明方向:针对给定的样本{Xi},其误差最小,即预测输出{Y_pred}与样本真实值{Yi}尽可能的接近,尽可能的相似。loss值越小,相似度越高,误差越小。
在实际工程中,由于{Y_real}是未知的,因此,在监督式学习中,使用样本标签{Yi}作为样本数据集{Xi}的真实值!!!!
由于实际样本数据集不是单个数据,因此,loss函数实际是所有样本误差的平均,反映的是模型对样本数据集中所有样本的预测映射关系 {Xi -> Yi_pred},与已知的样本标签的映射关系{Xi -> Yi_pred}整体的相似程度,而不是单个样本的相似程度!!!!
![]() 在相同的应用场合,描述相似程度的loss数学函数不尽同。
在相同的应用场合,描述相似程度的loss数学函数不尽同。
在不同的应用场合,描述相似程度的loss数学函数不尽同。
因此就有各种不同的loss函数,如均方差损失 Mean Squared Loss、平均绝对误差损失 Mean Absolute Error Loss、Huber Loss、分位数损失 Quantile Loss、交叉熵损失函数 Cross Entropy Loss、Hinge 损失 Hinge Loss。
不同的损失函数的基本的函数表达式、原理、特点并不相同方面。
因此,损失函数研究的是:如何表达两个函数(X-Y的映射关系称为函数)之间的相似程度的数学表达式。
因此,损失函数研究的是:如何表达两个函数(X-Y的映射关系称为函数)之间的距离远近的数学表达式。
1.4 本文重点阐述:
均方差损失 Mean Squared Loss、平均绝对误差损失 Mean Absolute Error Loss、Huber Loss。
这些损失函数主要应用于线性拟合或线性回归,而不是逻辑分类。
备注:
在本文中 Yi_pred也表示为![]()
第2章 平均绝对误差损失Mean Absolute Error Loss(MAE)
2.1 概述
描述两个函数之间距离远近最容易想到的就是:在相同的Xi输入下,两个函数输出Yi的差的绝对值。平均绝对误差损失正是基于这样的考虑。
2.2 loss函数的数学表达式
其数学函数表达式为:
平均绝对误差损失也称为 L1 Loss。
2.3 loss函数的几何图形与意义
![]()
从上图可以看出:
- loss函数值与(Yi-Yi_pred)值之间的关系是线性关系。
- MAE函数是有最小值的。
- 当Yi-Yi_pred>0时,其导数(梯度)恒定为1,也就是任意点的梯度值与离loss最小值的距离远近没有关系。
- 当Yi-Yi_pred<0时,其导数(梯度)恒定为-1,也就是任意点的梯度值与离loss最小值的距离远近没有关系。
- 当Yi-Yi_pred=0时,其导数(梯度)恒定为0。
2.4 特点
第3章 均方差损失 Mean Squared Error Loss(MSE)
3.1 概述
3.2 loss函数的数学表达式
均方差损失也称为 L2 Loss。
3.3 loss函数的几何图形与意义
(1)一元模型
![]()
(2)多元函数
![]()
从上图可以看出:
- loss函数值与(Yi-Yi_pred)之间的关系是非线性的平方关系,也就是说MSE具有对(Yi-Yi_pred)放大的作用。
- 该MSEloss函数是有最小值的,多元函数的损失函数:有可能有多个极小值,有一个最小值。
- 任意点的(Yi-Yi_pred)误差越大,该点处的导数(梯度)越大,迭代迭代时的步伐越大,当大于1时,MSE函数的梯度具有放大作用,收敛越快,大步流星。
- 任意点的(Yi-Yi_pred)误差越小,该点处的导数(梯度)越小,迭代迭代时的步伐越小,当大于1时,MSE函数的梯度具有缩小作用,收敛越精细,收敛越慢,小步慢挪。
- 任意点的(Yi-Yi_pred)等于0时,该点处的导数(梯度)等于0,为极小值。
3.4 特点
第4章 MSE与MAE的比较
![]()
上图是 MAE 和 MSE 损失画到同一张图里面。
- MAE 损失与绝对误差之间是线性关系。
- MSE 损失与误差是平方关系。
- 当误差非常大的时候,MSE 损失会远远大于 MAE 损失。因此当数据中出现一个误差非常大的离群值outlier 时,MSE 会产生一个非常大的损失和梯度,对模型的训练会产生较大误导性影响,优点是,收敛速度快,快速逼近离群值(辩证的看,这其实不是一件好事:粗枝大叶)。
- 当误差非常小的时候,MSE 损失会远远小于 MAE 损失。因此当数据中出现一个误差非常小的理想值是,MSE 会产生一个非常小的损失和梯度,说明模型的相似度越好,逼近理想目标值的精度越高,缺点是收敛变慢(辩证的看,这其实是一件好事:慢工出细活)。
第5章 平滑平均绝对误差Huber Loss (SMAE)
5.1 概述
MSE 损失收敛快但容易受 outlier 影响。
MAE 对 outlier 更加健壮但是收敛慢。
Huber Loss 则是一种将 MSE 与 MAE 结合起来,取两者优点的损失函数,也被称作 Smooth Mean Absolute Error Loss (SMAE)。
其原理和规则很简单:
当样本Xi的误差小于1或接近于0时,其误差使用MSE来计算。
当样本Xi的误差大于1或更大时,其误差使用MAE来计算。
SMAE优缺点:
优点是:获取更高的训练后模型精度,训练后的模型与目标的相似度高。
缺点是:牺牲了模型训练的时间,模型收敛相对于MSE变慢,需要更长的时间对模型进行训练。
如何同同一个函数,同时能够表达上述的规则呢?
5.2 SMAE的loss函数的数学表达式 - 方法1
(1)数学表达式
(2)几何图形与物理意义
- 当|Yi-Yi_pred| < (Yi-Yi_pred)^2 时,表明在下方, (Yi-Yi_pred)^2放大了误差效果,loss函数采用|Yi-Yi_pred| 。
- 当|Yi-Yi_pred| > (Yi-Yi_pred)^2 时,(Yi-Yi_pred)^2缩小了误差效果,loss函数采用(Yi-Yi_pred)^2 。
- 当|Yi-Yi_pred| = (Yi-Yi_pred)^2 时,表明是相交点,采用|Yi-Yi_pred|和(Yi-Yi_pred)^2是等效的。
(3)主要优缺点
优点:这种方法简洁、明了。
缺点:规则僵化,不可控,不可调,只能根据|Yi-Yi_pred| 与 (Yi-Yi_pred)^2的大小关系,选择loss函数的来源,是|Yi-Yi_pred|还是(Yi-Yi_pred)^2。
SMAE并没有采样上述方法,而是采用了更加灵活的方案,如下方法2:
5.2 SMAE的loss函数的数学表达式 - 方法2
(1)数学表达式
或表示成:
该种方法的特点:
- 选择条件:SMAE的loss函数的值,对于某个样本,选择MAE还是MSE,直接取决于|Yi - Yi_pred|绝对值的大小,而不是|Yi - Yi_pred|与 (Yi - Yi_pred)相对值的大小。
- 控制条件:这种方法选择条件,可以通过超参数θ来控制,当|Yi - Yi_pred|绝对值小于θ,loss函数值,来自于MAE, 即|Yi - Yi_pred|; |Yi - Yi_pred|绝对值大于θ, loss函数值来自于(Yi - Yi_pred)^2. |Yi - Yi_pred|绝对值等于θ,使得 |Yi - Yi_pred| == (Yi - Yi_pred)^2, 确保loss函数是连续的、可导的。这就是为什么公式中出现 -1/2*θ^2的原因。
(2)几何图形与物理意义
- 该函数有最小值
- 当 |Yi - Yi_pred| < θ, Loss = MSE" = 1/2 *(Yi - Yi_pred) *2
- 当 |Yi - Yi_pred| > θ, Loss = MAE" = θ * |Yi - Yi_pred| - 1/2 * θ*2
- 当 |Yi - Yi_pred| = θ, MSE = 1/2 *(Yi - Yi_pred) ^2 = 1/2 * θ ^2; MAE" = θ * |Yi - Yi_pred| - 1/2 * θ^2 = θ * θ - 1/2 * θ^2 = 1/2 * θ^2; => MSE" = MAE" = 1/2 * θ ^2, 即Loss函数在 |Yi - Yi_pred| = θ是连续的。
- θ是超参数,程序员可以控制。
5.3 特点
使用MSE训练神经网络的一个大问题是它的持续大梯度,这可能会导致在使用梯度下降训练结束时丢失最小值。对于MSE,当损失接近其最小值时,梯度减小,使其更加精确。
在这种情况下,Huber损失是非常有用的,因为它在减小梯度的最小值附近弯曲。它比MSE对离群值更稳健。因此,它结合了MSE和MAE的优良性能。然而,Huber损失的问题是我们可能需要训练超参数delta,这是一个迭代过程。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120478132
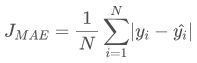
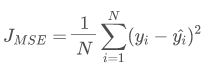

![[人工智能-深度学习-9]:神经网络基础 - 常见loss损失函数之均分误差MSE、绝对值误差MAE、平滑平均绝对误差Huber_第1张图片](http://img.e-com-net.com/image/info8/b9305a1cd8124d8883f7280d1203acbd.jpg)
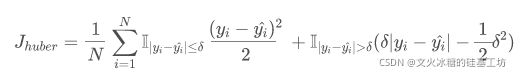
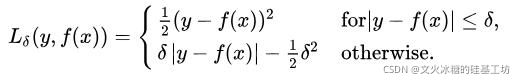
![[人工智能-深度学习-9]:神经网络基础 - 常见loss损失函数之均分误差MSE、绝对值误差MAE、平滑平均绝对误差Huber_第2张图片](http://img.e-com-net.com/image/info8/cd15db8397314edbb1e19cdf1b3b1e1f.jpg)