数学文化赏析学习笔记
数学之魂
数学的对象与方法
数学的思想与方法
数学的特点与地位
1、概念的抽象性
2、推理的严密性
3、结论的确定性
4、数学的地位:基础性、普适性、可靠性
tips:
演绎推理是收敛性思维
类比推理是发散性思维
归纳推理是从个体认识群体的推理,从特殊到一般
属于拓扑变换的有:橡皮筋拉伸、纸张折叠;
数与形是数学的两大基石
数学之功
数学的功能
实用、教育、语言、文化:
语言功能
数学语言包括:符号、公式、法则、定理、方程。。。
特点:简单化、清晰化、扩展化
文化功能
深化人类对世界的认识,推动人类物质、精神文明的发展
升华人类的精神和品格
1、深入到社会的每个角落
2、是人类创造并且传承下来的知识、方法、思想
3、影响着人类的思想
数学文化的内涵:知识性成分、观念性成分
数学的价值
1、教学与个人成长
数学意识、数学语言、数学技能
数学思维的特点:抽象性、创造性、逻辑性、形式化
抽象化(抓共性、看本质):速度=x/t、切线=y/x
逻辑性:演绎推理(精细严谨)
形式化:抓本质共性、建立统一模型
2、数学与人类生活
提高效率、解释疑问、理智判断、科学决策
exp:
三条腿的椅子一定能在不平整的地板上放稳
四条腿(等长)的椅子一定能在不平整的地板上放稳
3、数学与科技发展
数学是科学的语言(建模)
数学孕育科学
exp:万有引力定律、相对论、黑洞理论、奇性理论、分子生物与拓扑学、数量遗传学
数学是科学的工具
exp:地质勘查、污染问题
4、数学与社会进步
数学工具是促进物质文明的重要力量
数学理性是促进精神文明的重要因素
数学美学是促进艺术发展的重要基础
数学之旅
数学的分类
1、从历史看
初等数学和古代数学(16世纪以前)
古希腊建立的欧式几何学
古代中国、古印度、古巴比伦时期建立的算术
欧洲文艺复兴时期发展起来的代数方程
变量数学(17--19世纪初期,数形结合)
17世纪,笛卡尔建立了解析几何(标志)
微积分
特点:从静态到动态、从逻辑到代数
近代数学(19世纪)
五次及以上的代数方程不存在通用的求根公式
几何的非欧化
对之前数学的提升与完善
现代数学(20世界)
1900年希尔伯特提出了23个数学问题(起点)
基础:Cantor集合论
特征:
单变量到多变量、低维到高维
从线性到非线性
局部到整体,简单到复杂
连续到间断,稳定到分叉
精确到模糊
计算机的应用
趋势:逐步走向统一、分支增加、表现形式抽象化
2、从对象与方法看
基础数学(代数、几何、分析)
应用数学
计算数学(计算的方法)
概率统计(随机)
运筹与控制论(管理)
数学的分支发展概观
1、几何学通论
思辨方法:欧几里得几何学
代数方法:笛卡尔的解析几何
向量几何:不依赖于坐标系
分形几何学:计算机的应用
2、代数学大观
起源于古代中国和古埃及
初等代数学
高等代数学:线性代数、多项式代数
3、微积分大意
微积分:17世纪英国数学家牛顿、德国数学家莱布尼茨分别独立建立
研究对象为函数
研究工具为极限
研究内容:微分、积分、微积分基本定理
4、随机数学与模糊数学
随机数学:研究确定性与不确定性
模糊数学:研究事物的程度
数学的形成与发展因素
实用、科学、哲学、美学
tips:
近代数学的特点有:
数学之理
数学思维及其价值
发散性思维:类比、归纳、迁移、想象
感性、感性、感觉
具有或然性、创造性
属于合情推理
收敛性思维:三段论、反证法、数学归纳法
理性
具有必然性、正确性
属于演绎推理
数学故事话思维
1、数学关注什么
追求真理、正确、规律、准确、本质
2、数学如何思考
化归思想:未知-->已知
复杂-->简单
抽象-->具体
类比思想
归纳、演绎
逆向思维
假设、推理、反证
3、数学如何表达
严谨
数学游戏话思维
1、躲三十
exp:
只有一堆石子的情况,假定石子的总数为30。
甲赢则需要在最后取走第26颗石子,方能利于不败之地。对于26颗石子,则需要取走第22颗石子才能在下一轮取走第26颗石子。以此类推需要分别取走第26、22、18、14、10、6、2颗石子。因此需要先手取两颗石子,方能立于不败之地。
2、取石子
exp:
对于只有一堆石子的情况,假定石子的总数为30。
甲赢则需要在最后取走第26颗石子,方能利于不败之地。对于26颗石子,则需要取走第22颗石子才能在下一轮取走第26颗石子。以此类推需要分别取走第26、22、18、14、10、6、2颗石子。因此需要先手取两颗石子,方能立于不败之地。
对于N堆石子的情况,只要保证任意序号的石子堆对(1+3)的取模结果相同,则可以确定该序号的石子堆可以取胜。
序号为A的石子堆为18个,序号为B的石子堆为22个,甲取在任意堆中取任意个石子,乙在另一堆中取相同数量的石子,即可保证A和B的石子数量对(1+3)取模结果相同,这样就可以保证胜局。
3、变形取石子
exp:
规则:每人每次可以在其中一堆中取走任意多颗石子,取走最后一颗石子的人获胜。(一次只能在其中一堆中取石子,同时也不得不取石子)
对于只有一堆石子,先手的人获胜
对于两堆石子,保证两堆石子的数量相同即可锁定胜局
对于三堆石子,有:
a、至少有两堆石子数量相同。先手将剩下的一堆不同数量的石子取完,留给对方两堆相同的石子。
b、三堆石子互不相同。留给对方1、2、3个石子的局面即可锁定胜局-->留给对方(1,2m,2m+1)为赢局。
4、取石子赢局特征
转换为二进制,相加,留下偶型残局一定是赢局(相加结果的各个位都是偶数,此处不做进位处理)。
奇型残局(相加结果的各个位存在至少一个奇数,此处不做进位处理)。
原因:1、偶型残局取子后一定变为奇型残局;
2、任何的奇型残局,一定有一种取法,使得取子后变为偶型残局。
tips:
数学之辩
动中有静
1、一个魔术
公理-->推理-->定理
2、动中有静
exp:轴对称、旋转、不动点定理
变中有恒
1、变化中的常数
凸多边形的外角和为360°
内角和为:(n-2)*180°
欧拉公式:f-e+v=2
面数-顶点数+边数=2
在平面上:f-e+v=1
三角形的面积:S=sqrt(p(p-a)(p-b)(p-c))
p=(a+b+c)/2
2、变化中的关系
3、变化中的恒等
化归,抓住事物的不变部分。
乱中有序
异中有同
情中有理
蜂窝建造、鸽子原理
一个聚会当中,一定有两个人在场的朋友数量相同
理中有用
平均:算术平均用于分配
几何平均用于几何
调和平均用于音乐
欧拉定理
反证法
tips:
数学之美
美的根源于特征
1、美的感性特征(外在)
简洁性、和谐性、奇异性
2、美的理性特征(内在)
具有社会性
3、数学美的根源
数学关注本质、共性、规律、联系,具有简洁、和谐之美
数学反映自然、社会,重视变化、特例,具有奇异之美
4、如何欣赏数学美
思考、思维
5、数学的简洁之美
符号美:阶乘、幂将算式的表达形式简单化
常数美:f-e+v=2
统一美:克莱因用变化群的观点统一了十九世纪的几何学
6、数学的和谐之美
对称美、序列美、节奏美
exp:导数与积分、矩阵转置与反函数
7、数学的奇异之美
有限美、神秘美、对比美、滑稽美
数学方法之美
1、认识的飞跃
2、演绎法之美
3、类比法之美
4、数形结合之美
勾股定理
5、此处无形胜有形
存在性证明:构造性证明、纯理性证明
抽屉原理、排中律
6、从低级数学到高级数学
数学结论之美
1、三角形之美
稳定性、三角形的五心
2、圆形之美
3、矩形之美
黄金分割:制作五角星 0.618
4、斐波那契数列之美
对于斐波那契数列:an+1=an*1.618
exp:爬楼梯,计算爬楼梯的方法数量:an=an-1+an-2
斐波那契数列的第n+1项可以通过n阶行列式进行表示
积:任何相邻两项之积等于该较小项及其前各项平方和
an *an+1-an *an-1=an^2
an*an+1=an^2+an-1^2+......+a1^2
任何相隔两项之积等于其中间数的平方+1 -1
an-1*an+1=an^2+(-1)^n
任何间隔奇数个项的两项之积等于其中间数的平方+1 -1
an-2*an+2=an^2+(-1)^n+1
商:任何相邻前后两项之商趋于一个稳定的数值 0.618
任何相邻后前两项之商趋于一个稳定的数值 1.618
各项被某数除的余数是周期的,每有限项一循环(以递归的形式生成的数列也满足该性质)
斐波那契数列的前n项和:a1+a2+......+an=an+2-a2
am+am+1+...+an=an+2-am+1
任何相邻10项之和等于这10项中第7项的11倍
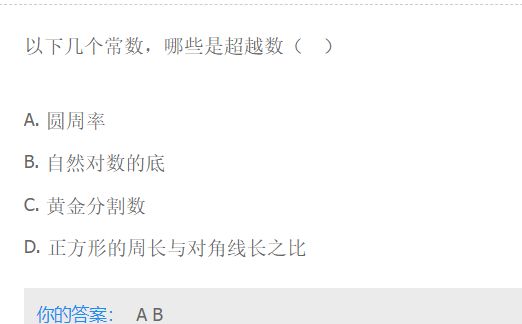
5、自然对数的底
tips:
数学之奇
实数系统
1、数系扩充概述
数是数学的两大基石之一。数的产生和发展源自于实用需求或数学自身发展需求。
无理数的承认在公元前4世纪。
2、有理数集
有限小数、无限循环小数。
所有的正整数和正偶数一样多(可以一一对应:n=2n)
所有的正整数和平方数一样多
有理数集是可数集
有理数集的长度为0
有理数是封闭的
3、实数集
实数是封闭的
实数集是不可数集,不能与自然数建立一一对应
4、无限集合的基数
可数集基数N0的运算性质:No+n=No
No+No=No,nNo=No
No^n=No
代数数集是可数集
实数集是不可数集,基为N1(连续统基数)
运算性质:N1+n+No=N1
N1+N1=N1,nN1=N1
NoN1=N1, N1^n=N1
5、认识超穷数
Nx=2^Nx-1
6、连续统假设
三种几何并存
1、欧几里得几何
2、非欧几何
罗巴切夫斯基将平行公理(第五公理)改为过直线外一点可以作两条直线与之不相交。(非欧几何开始的标志)
黎曼几何
3、三种几何对比
罗氏几何:适用于太空或原子核世界 小于180° 三角形面积大
欧式几何:日常小范围内 180°
黎曼几何:地球上远距离旅行 大于180° 三角形面积小
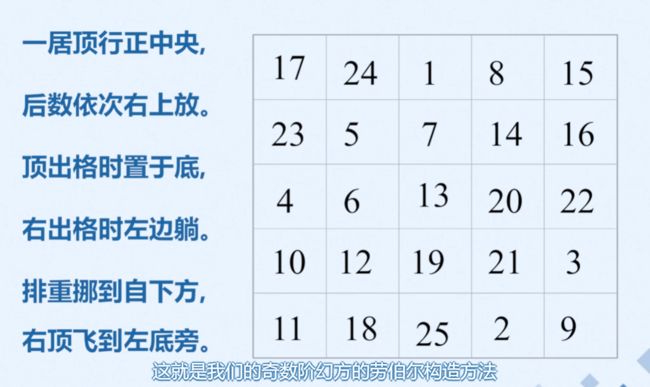
河图洛书与幻方
1、认识幻方
洛书:任意横竖斜各条直线上的三个数之和均等于15
二阶幻方不存在,3阶幻方只有一种,4阶幻方有880种
若幻方各个数是从1到n^2的连续自然数,则称之为标准幻方
n阶标准幻方的幻和为:n*(n^2+1)/2
神奇、启发智力、应用之需
分类(阶数):奇数阶幻方、偶数阶幻方
偶数阶幻方:双偶阶幻方、单偶阶幻方
分类(性质):平方幻方(双重幻方)、和积幻方(乘积幻方)
2、构造幻方
奇数阶幻方的构造:九子斜排,上下对易,左右相更,四维挺进
exp:
奇数阶幻方:
exp:
偶数阶幻方的构造方法:
海尔构造法:
然后将方阵B进行转置,得到方阵C
接着把方阵C中的每一个数分别用其相对应的根数进行替换,得到新的方阵D (根数=n(p-1))
最后将方阵B和方阵D相加,得到一个n阶的幻方E
双偶阶幻方的构造方法:
补数=n^2+1-p(n为阶数)——esp:四阶幻方当中,1的补数为16, 9的补数为8
1、将1到n^2依次填入到方阵的各个方格内(从左到右,从上到下)
2、分别在对角线做出一条线,然后连接四条边的中点,得到一个正方形。
3、将在线上的所有数,换成其补数
3、欣赏幻方
tips:
数学之趣
数字之趣
数字黑洞:经过若干规则的操作后,得到的结果相同
卡普雷卡黑洞6174(495,只需要6个循环;09):任意选择一个四位数(数字不能全相同),把所有的数字从大到小排列,再把数字从小到大排列,用前者减去后者,得到一个新的数字,重复上述操作。7个循环之内,必然会得到6174。(大数减去小数为9的倍数)
123黑洞(西西弗斯串):任意取一个数,算出它的偶数个数,奇数个数以及总位数,按照(偶、奇、总)排列,得到一个新的数,重复上述过程,最终必将得到一个123的结果。
153黑洞:任意取一个3的倍数,求其个位数字的立方和为新的数,对新数重复上述过程,最终必定会得到153这个结果。
1与4黑洞:任意一个自然数,求其各位数字的平方和为新的数,对新书重复上述过程,最终的结果必定是1或者4。
3x+1问题:对任意自然数,若为偶数,则除以2,否则乘3+1,重复上述操作,最终结果必然是1。
数形之趣
1、勾股定理——几何观点
几何学有两大宝藏:勾股定理(毕达哥拉斯定理)、黄金分割。
中国证明勾股定理:出入相补图
2、勾股定理——代数观点
在边长是整数的直角三角形中:勾股中必定有一个数是3的倍数
勾股中必定有一个数是4的倍数
勾股弦中必定有一个数是5的倍数
不存在勾股同时是奇数,而弦为偶数的组合
弦与勾股中某一个数的和、差均为完全平方数
3、勾股定理——勾股数趣谈
除了1和2之外,任何一个自然数都可以作为整数边长直角三角形的一个直角边边长
逻辑之趣
1、悖论起源与定义
从自身的结论出发可以导出矛盾的事实。
芝诺悖论、说谎悖论
2、悖论与数学发展
第一次数学危机:对于无理数的认识
第二次数学危机:微积分的危机(方法论的变革)
第三次数学危机:对于集合论的认识(认识论的不严谨)
3、悖论示例与启示
悖论无法避免、悖论可以解决
条件收敛级数不满足交换律
数学、游戏与魔术
1、有和无——二进制魔术
exp:10111——>第1、2、3、5张表格有,其他表格没有
2、奇与偶——动了哪张牌
3、序与数——你两的秘密我知道
tips:
数学之妙
数学归纳法原理
数学归纳法变形:
假定An和Bn是自然数相关的两种命题,如果:
(1)当n=1时命题A1是成立的;
(2)假设当n=k时,命题Ak是成立的,可以证明命题Bk也是成立的;
(3)假设当n=k时命题Bk是成立的,可以证明当n=k+1时命题Ak+1也是成立的
那么命题An、Bn对所有的自然数n都是成立的。
两色定理:在一张纸上随意画一些直线,这些直线把这张纸分割成若干个区域。
把这假象成一个世界地图,只要对其填色以便区分各个不同的国家,只需要两种颜色就够了。
反证法与抽屉原理
反证法是间接证明法
反证法的依据是逻辑思维中的矛盾律和排中律
抽屉原理——>鸽笼原理
任意给定的三个整数中,必定有两个整数其和为偶数
任意给定的5个整数中,必定有3个整数,其和是3的倍数
在坐标平面上,任意取5个整点,则必定存在其中两个整点,其连线的中点仍然是整点
在n维空间中,任意取2^n+1个整点,则必定存在其中两个整点,其连线的重点仍然是整点
在任意的6个人中,一定有3个人互相都认识或者互相都不认识
七桥问题与一笔画定定理
七桥问题既不是代数问题,也不是平面几何问题
一个图可以一笔画的充要条件是:奇点的个数为0或2
图论、拓扑学(位置几何学,不关心具体的形状,只关注点与点的位置关系)
数论与密码
加密方法:代换法
RSA编码方法:大数分解是极端困难的
过程:(1)对方将明文转化为密文y:x^n=y(modN)
(2)对方发送密文y
(3)我方收到密文y后转化为明文x:y^m=x(modN)
数学之问
古代三大几何难题
1、化圆为方
2、三等分任意角
3、倍立方体(作一个立方体,其体积为一已知立方体的两倍)
1637年笛卡儿创建解析几何以后,许多几何问题都可以转化为代数问题来研究。1837年旺策尔(Wantzel)给出三等分任一角及倍立方不可能用尺规作图的证明。1882年林得曼(Linderman)也证明了π的超越性(即π不为任何整数系数多次式的根),化圆为方的不可能性也得以确立。
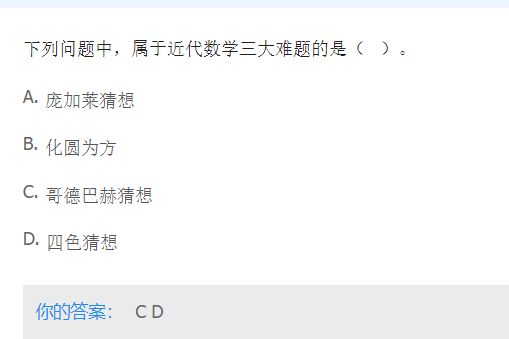
费马猜想
费马猜想:当整数n>2时,关于x^n+y^n=z^n没有正整数解。(1637年左右)
欧拉证明了当n=3的时候,费马猜想是成立的,发表在《代数指南》中,方法是“无限下降法”
已经解决
哥德巴赫猜想
哥德巴赫猜想:任意一个大于5的整数都可以写成三个质数之和
常用的说法:任意一个大于2的偶数都可以写成两个质数之和
把命题"任一充分大的偶数都可以表示成为一个素因子个数不超过a个的数与另一个素因子不超过b个的数之和"记作"a+b"。1966年陈景润证明了"1+2"成立,即"任一充分大的偶数都可以表示成二个素数的和,或是一个素数和一个半素数的和"。
尚未解决
四色猜想
已经被解决
庞加莱猜想
拓扑学(佩雷尔曼已经解决该猜想)
庞加莱猜想是一个拓扑学中带有基本意义的命题,将有助于人类更好地研究三维空间,其带来的结果将会加深人们对流形性质的认识。
1904年,法国数学家亨利·庞加莱提出了一个拓扑学的猜想:
“任何一个单连通的,闭的三维流形一定同胚于一个三维的球面。”
简单的说,一个闭的三维流形就是一个有边界的三维空间;单连通就是这个空间中每条封闭的曲线都可以连续的收缩成一点,或者说在一个封闭的三维空间,假如每条封闭的曲线都能收缩成一点,这个空间就一定是一个三维球面 [1] 。
后来,这个猜想被推广至三维以上空间,被称为“高维庞加莱猜想”。
黎曼猜想
尚未被解决
近代数学三大难题:费马猜想、四色猜想、哥德巴赫猜想