论文笔记NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

NeRF使用神经网络来表示场景。给定一个场景，输入该场景一些视角的图片，NeRF可以合成该场景新视角的图片。

神经辐射场

神经辐射场（neural radiance field，NeRF）使用5D的向量值函数表示一个场景。
输入是连续的5D坐标（包括位置$\mathbf{x}=(x,y,z)$和视角方向$\mathbf{d}=(\theta ,\varphi )$），输出是发光颜色$\mathbf{c}=(r,g,b)$和体积密度$\sigma$。
具体地，用一个全连接网络近似这个场景，也就是学习 $F_{\Theta }:(\mathbf{x},\mathbf{d})\to (\mathbf{c},\sigma )$。
作者鼓励让体积密度只依赖于位置。所以网络结构是先输入位置$\mathbf{x}$，输出$\sigma$和一个特征向量。之后将特征向量和视角方向拼接，最后映射到$\mathbf{c}$颜色。
注意对每一个场景需要训练一个NeRF。

位置编码

在将输入传递到网络之前，使用高频函数将输入映射到更高维空间可以更好地拟合包含高频变化的数据。所以，类似Transformer，作者提出将$\mathbf{x},\mathbf{d}$用三角函数映射到高维空间中，再输入网络：

$p$是每个坐标的值，比如$\mathbf{x}$中的$x,y,z$。

使用辐射场进行立体渲染

为了配合辐射场，作者采用立体渲染（volume rendering）方法渲染图像。
关于立体渲染可以参考 https://zhuanlan.zhihu.com/p/595117334
体积密度$\sigma (\mathbf{x})$可以解释为光线在位置$\mathbf{x}$处终止于无穷小粒子的微分概率。
立体渲染中，相机光线$\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}$在范围$[t_n,t_f]$的期望颜色$C(\mathbf{r})$如下计算：
$$\begin{gathered} C(\mathbf{r})={\int }_{t_n}^{t_f}T(t)\sigma (\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt \\ whereT(t)=\exp (-{\int }_{t_n}^t\sigma (\mathbf{r}(s))ds) \end{gathered}$$从连续的神经辐射场渲染一个视角，需要追踪所需虚拟相机的相机光线上的每个像素，来估计积分$C(\mathbf{r})$。

上面公式的积分实际中用数值方法计算，需要采样求和。但如果固定在某些点采样，会限制表示的分辨率。为了解决这个问题，作者提出使用分层采样（stratified sampling）的方法。首先将$[t_n,t_f]$平分成N个大小一样的桶，然后在每个桶中随机采样一个样本：
$$t_i\sim \mathcal{U}[t_n+\frac{i-1}{N}(t_f-t_n),t_n+\frac{i}{N}(t_f-t_n)]$$虽然采样的样本还是离散的，但是优化过程是循环的，需要进行多次采样，每次采样可以采样到不同的位置，所以相当于在连续的位置优化。用采样的样本估计$C(\mathbf{r})$的方法如下：
$$\begin{gathered} \hat{C}(\mathbf{r})=\sum _i^N{T}_i(1-\exp (-{\sigma }_i{\delta }_i)){\mathbf{c}}_i \\ where{T}_i=\exp (-\sum _{j=1}^{i-1}{\sigma }_j{\delta }_j)\text{\hspace{1em}(1)} \end{gathered}$$其中${\delta }_i=t_{i+1}-t_i$。另外，估计$C(\mathbf{r})$的方法是可导的，所以可以方便的优化参数。

Hierarchical立体采样

如果沿每个相机光线的 N 个查询点密集地计算NeRF的值，这样的渲染策略是效率低下的，因为对渲染图像没有贡献的自由空间和遮挡区域会被重复采样。
为了解决这个问题，作者提出训练两个网络，一个是粗粒度（coarse）的，一个细粒度（fine）的。首先对粗粒度网络分层采样$N_c$个点，然后计算${\hat{C}}_c(\mathbf{r})$。
标准化${\hat{w}}_i=\frac{w_i}{{\sum }_j{w}_j}$，可以得到一个分布的概率密度函数。根据这个分布，用逆变换采样（inverse transform sampling）得到$N_f$个点。这$N_f$个点是根据其对渲染的重要性得到的。
然后，用细粒度网络计算这$N_c+N_f$个点的值，用公式(1)计算最终的光线颜色${\hat{C}}_f(\mathbf{r})$。
这种Hierarchical的方式可以对可见部分采样更多的点。

训练

每一个场景需要单独训练一个NeRF。输入除了场景的一组RGB图像，还有其对应的相机位置、相机内参、场景边界。
训练的损失函数是渲染像素和真实像素的平方误差：

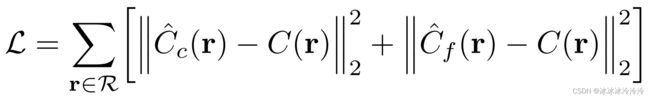
其中$\mathcal{R}$是一个batch的光线集合。在训练的每个循环中，从像素中随机采样一个batch的相机光线。
虽然最后渲染的图像由细粒度网络产生，但是粗粒度网络同样需要训练，因为粗粒度网络提供了采样点的位置。