伸展树(Splay树)
伸展树(Splay树)
时间复杂度: O(logn)
目录
一、旋转
1.1单L旋转
1.2单R旋转
1.3LL双旋
1.4RR双旋
1.5RL双旋
1.6LR双旋
二、伸展
三、查找
四、插入
五、删除
六、完整代码
一、旋转
1.1单L旋转
思路
遇到如下情况,查找的元素是9,其父节点是7并且是根结点,所以这种情况只需对其父结点左旋一次,要查找的元素便变成了根结点
代码实现
//SplayTree结点实现
typedef struct SpalyTreeNode
{
int val;
Tree parent;
Tree lchild;
Tree rchild;
SpalyTreeNode(int v) : val(v), parent(nullptr), lchild(nullptr), rchild(nullptr) {}
}*Tree;
//返回当前子树中的新根
Tree left_single_rotate(Tree& root, Tree node)//这里root传引用的目的是,当node旋转之后是根结点,就将root改为node
{
if (!node)
{
return nullptr;
}
Tree parent = node->parent;
Tree pparent = parent->parent;
parent->rchild = node->lchild;
if (node->lchild)
{
node->lchild->parent = parent;
}
node->lchild = parent;
parent->parent = node;
node->parent = pparent;
if (pparent)//parent不是根结点
{
if (parent == pparent->lchild)
{
pparent->lchild = node;
}
else
{
pparent->rchild = node;
}
}
else//parent是根结点
{
root = node;
}
return node;
}
返回目录
1.2单R旋转
思路
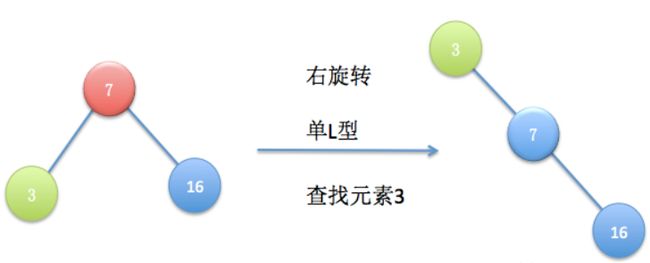
与单L是对称的,要查找的结点是根结点的左子树,它的父结点是根结点,这样向右旋转一次,要查找的结点就到了根结点的位置
代码实现
//返回当前子树的新根
Tree right_single_rotate(Tree& root, Tree node)
{
if (!node)
{
return nullptr;
}
Tree parent = node->parent;
Tree pparent = parent->parent;
parent->lchild = node->rchild;
if (node->rchild)
{
node->rchild->parent = parent;
}
node->rchild = parent;
parent->parent = node;
node->parent = pparent;
if (pparent)
{
if (parent == pparent->lchild)
{
pparent->lchild = node;
}
else
{
pparent->rchild = node;
}
}
else
{
root = node;
}
return node;
}
返回目录
1.3LL双旋
思路
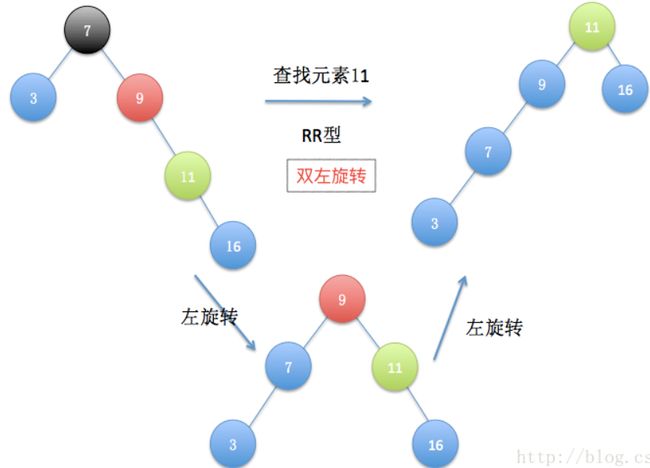
遇到如下情况,查找的元素11,注意顺序先旋转其父亲,再旋转自己,具体顺序原因在下面有说明,这样要查找的元素就成为了子树的根结点
先旋转父亲,再旋转自己的原因是为了减小树的高度
代码实现
void left_double_rotate(Tree& root, Tree node)
{
left_single_rotate(root, node->parent);
left_single_rotate(root, node);
}
返回目录
1.4RR双旋
思路
与LL双旋对称
代码实现
void right_double_rotate(Tree& root, Tree node)
{
right_single_rotate(root, node->parent);
right_single_rotate(root, node);
}
返回目录
1.5RL双旋
思路
遇到如下情况,先旋转自己,再旋转新的自己,与AVL树一致
实现代码
void RL_rotate(Tree& root, Tree node)
{
right_single_rotate(root, node);
left_single_rotate(root, node);
}
返回目录
1.6LR双旋
思路
与RL对称
代码实现
void LR_rotate(Tree& root, Tree node)
{
left_single_rotate(root, node);
right_single_rotate(root, node);
}
返回目录
二、伸展
思路
当我们查找到一个val后,如果它不是根结点,我们需要对它进行伸展,直到将它伸展到根结点处
代码实现
void up(Tree& root, Tree node)
{
Tree parent = node->parent;
Tree pparent = parent->parent;
int i = 0;
int j = 0;
i = (pparent->lchild == parent ? -1 : 1);
j = (parent->lchild == node ? -1 : 1);
if (i == -1 && j == -1)
{
right_double_rotate(root, node);
}
else if (i == -1 && j == 1)
{
LR_rotate(root, node);
}
else if (i == 1 && j == 1)
{
left_double_rotate(root, node);
}
else
{
RL_rotate(root, node);
}
}
void SplayTree(Tree& root, Tree node)
{
while (root->lchild != node && root->rchild != node && root != node)
{
up(root, node);
}
if (node == root->lchild)
{
right_single_rotate(root, node);
}
else
{
left_single_rotate(root, node);
}
}
返回目录
三、查找
思路
首先通过内部的查找函数找到val的结点,如果找到并且该结点不为根结点,就要SplayTree,否则就返回
代码实现
Tree* search_val(Tree& root, int val, Tree& parent)
{
if (!root)
{
return &root;
}
if (val < root->val)
{
return search_val(root->lchild, val, parent = root);
}
else if (root->val < val)
{
return search_val(root->rchild, val, parent = root);
}
else
{
return &root;
}
}
bool search(Tree& root, int val)
{
if (!root)
{
return false;
}
Tree parent = nullptr;
Tree* tmp = search_val(root, val, parent);
if (*tmp)
{
if (*tmp != root)
{
SplayTree(root, *tmp);
return true;
}
else
{
return true;
}
}
else
{
return false;
}
}
四、插入
思路
首先先查询应该插入元素的位置,如果此位置为空,就插入,否则,返回false
代码实现
bool insert(Tree& root, int v)
{
Tree parent = nullptr;
Tree* tmp = search_val(root, v, parent);
if (!(*tmp))
{
Tree node = new SpalyTreeNode(v);
*tmp = node;
(*tmp)->parent = parent;
return true;
}
else
{
return false;
}
}
返回目录
五、删除
思路
首先找到要删除的元素并把它伸展至根结点,然后判断它的右子树是否为空,如果为空,就直接删除;如果不为空,就找到根结点最近的后继,然后将他们的值互换,把那个后继的右子树赋值为当前值,然后删除那个后继
代码实现
Tree* find_Near(Tree& root)
{
if (root->lchild)
{
return find_Near(root->lchild);
}
return &root;
}
void remove(Tree& root, int v)
{
Tree parent = nullptr;
Tree* tmp = search_val(root, v, parent);
Tree* replace;
Tree replace2;
if (*tmp)
{
if (*tmp != root)
SplayTree(root, *tmp);
if (root->rchild)
{
replace = find_Near(root->rchild);
root->val = (*replace)->val;
//左子树必然为空
replace2 = (*replace);
(*replace) = (*replace)->rchild;
delete replace2;
}
else
{
replace2 = root;
root = root->lchild;
delete replace2;
}
}
}
返回目录
六、完整代码
#include 运行结果: