【声源定位】 球面散乱数据插值方法/似然估计hybrid spherical interpolation/maximum likelihood (SI/ML) 麦克风阵列声源定位

1.软件版本

MATLAB2021a

2.本算法理论知识点

球面散乱数据插值方法/似然估计SI/ML

麦克风阵列声源定位

3.算法具体理论

这个部分的程序如下所示：

这个部分理论如下所示：

本文最后的算法是：

4.部分核心代码

clc;
clear;
close all;
warning off;
addpath 'func\'
 
load data\11_11_2KHz24cm_8cmArray.mat


x      = data;

figure(1);
plot(x(10000:12000,1),'b-o');hold on;
plot(x(10000:12000,2),'r-o');hold on;
plot(x(10000:12000,3),'k-o');hold on;
plot(x(10000:12000,4),'m-o');hold on;
plot(x(10000:12000,5),'b-s');hold on;
plot(x(10000:12000,6),'r-s');hold on;
plot(x(10000:12000,7),'k-s');hold on;
plot(x(10000:12000,8),'m-s');hold on;
legend('1','2','3','4','5','6','7','8');

[R,C]  = size(x);
M      = min(R,C); %阵元数目
N      = length(x);  
x_1    = x(1:N,:);
Delay  = zeros(M-1,1);
s_rate = 200000;
Fc     = 200e3;
LEN    = 2*N-1;%增加精度
CUT    = round(0.1*LEN);
%先计算标准值时刻位置
fft_x1           = fft(x_1(:,1),LEN);
fft_x1           = fft(x_1(:,1),LEN);
conj_x1          = conj(fft_x1);
Sxy              = fft_x1.*conj_x1;
Cxy              = fftshift(ifft(Sxy.*hamming(max(size(Sxy)))));
[Vmx0,location0] = max(abs(Cxy(CUT:end-CUT)));
 
for i = 1:M-1
    fft_x1         = fft(x_1(:,1),LEN);
    fft_xi         = fft(x_1(:,i+1),LEN);
    conj_x1        = conj(fft_x1);
    Sxy            = fft_xi.*conj_x1;
    Cxy            = fftshift(ifft(Sxy.*hamming(max(size(Sxy)))));
    [Vmx,location] = max(abs(Cxy(CUT:end-CUT)));

    %绝对值
    d1             = abs(location-location0);
    %真实值
    d2             = location-location0;
    %计算得到采样点间隔
    Delay1(i)      = d1;
    Delay2(i)      = d2;
end
 
%根据间隔，计算时间和距离延迟
times1 = Delay1./Fc;
dist1  = times1*345;
times2 = Delay2./Fc;
dist2  = times2*345;

disp('采样点个数延迟:');
Delay1
Delay2

disp('采样时间延迟:');
times1
times2

disp('采样距离延迟:');

dist1
dist2

save Gcc.mat Delay1  Delay2 times1 times2 dist1 dist2



%**************************************************************************
%**************************************************************************
%**************************************************************************
clear;
xs_src_actual   = [0]   ; 
ys_src_actual   = [0.32]; 
xi              = [0 0.08 0.16 0.24 0    0.08 0.16 0.24]; 
yi              = [0 0    0    0    0.08 0.08 0.08 0.08]; 
%调用前面的延迟估计
load Gcc.mat
%根据路程差计算声源
%number of Monte Carlo runs
nRun            = 100; 
%uncomment one of them
%turn off ML calculation 
bML             = 1;
%calculate corresponding range Rs
Rs_actual       = sqrt(xs_src_actual.^2 + ys_src_actual.^2);
bearing_actual  = [xs_src_actual; ys_src_actual]/Rs_actual; 
%number of sensor (>4)
temp            = size(xi); 
nSen            = temp(1,2); 
%RD noise (Choose 1)
Noise_Factor    = eps; % noise std = Std_Norm * (source distance). 
%we expect bigger noise variance for larger distance.
Noise_Var       =(Noise_Factor*Rs_actual)^2;
%Functions
%Random Process 
for k=1:nRun, % Monte Carlo Simulation
    Xi     = [xi' yi'];
    Di     = sqrt((xi-xs_src_actual).^2 + (yi-ys_src_actual).^2); 
    locSen = [xi' yi'];
    %using N sensors 
    for i=1:nSen-1
        d(i,1)     = Di(i+1)-Di(1);
        %噪声
        delta(i,1) = dist1(i);
        s(i,:)     = [xi(i+1) yi(i+1)];  
        Alpha_noise= (bearing_actual + randn(2,1)/15);
    end
    %set to identity matrix for unweighted case
    w               = eye(nSen-1); 
    Sw              =(s'*w*s)^(-1)*s'*w; 
    Ps              = s*Sw; 
    Ps_ortho        = eye(nSen-1)-Ps;
    %SI method 
    Rs_SI_cal       = 0.5*(d'*Ps_ortho*w*Ps_ortho*delta)/(d'*Ps_ortho*w*Ps_ortho*d);
    %Calculate Xs for SI method
    Xs_row_SI       = 0.5*Sw*(2*Rs_SI_cal*d-delta); 
    Xs_SI(k,:)      = [Xs_row_SI.*Alpha_noise]';
    Rs_SI(k,:)      = sqrt(Xs_SI(k,1)^2 + Xs_SI(k,2)^2);
    bearing_SI(k,:) = Xs_SI(k,:)/Rs_SI(k,:);
    %Maximum Likelihood Method
    if (bML==1)
        %As value obtained from SI as starting guess 
        x0      = Xs_SI(k,:);
        %x0 = [0 ys_src_actual 0]; % Starting guess
        %LevenbergMarquardt 
        options = optimset('Algorithm','Levenberg-Marquardt'); %LM
        x       = lsqnonlin(@mlobjfun,x0,[],[],options,locSen,Noise_Var,d); 
        Xs_ML(k,:)      = x;
        Rs_ML(k,:)      = sqrt(Xs_ML(k,1)^2+Xs_ML(k,2)^2);
        bearing_ML(k,:) = Xs_ML(k,:)/Rs_ML(k,:); 
    end
    %Calculate bias (i.e., errors) for source location, range and bearing 
    %SI 
    bias_Xs_SI(k,1) = Xs_SI(k,1) - xs_src_actual; 
    bias_Xs_SI(k,2) = Xs_SI(k,2) - ys_src_actual; 
    %ML
    if (bML==1)
        bias_Xs_ML(k,1) = Xs_ML(k,1)-xs_src_actual; 
        bias_Xs_ML(k,2) = Xs_ML(k,2)-ys_src_actual; 
    end
end

clc;


figure;

bias_Rs_SI = Rs_SI-Rs_actual;
bias_bearing_SI = 180/pi*acos(bearing_SI*bearing_actual);

if (bML==1)
bias_Rs_ML=Rs_ML-Rs_actual;
bias_bearing_ML = 180/pi*acos(bearing_ML*bearing_actual); 
end

meanxs_SI=mean(bias_Xs_SI(:,1)); 
meanys_SI=mean(bias_Xs_SI(:,2)); 
meanrs_SI=mean(bias_Rs_SI); 
meanbear_SI=mean(bias_bearing_SI);

vect_mean_SI=[meanxs_SI;meanys_SI;meanrs_SI;meanbear_SI];

%ML
if (bML==1)
meanxs_ML=mean(bias_Xs_ML(:,1)); 
meanys_ML=mean(bias_Xs_ML(:,2)); 
meanrs_ML=mean(bias_Rs_ML); 
meanbear_ML=mean(bias_bearing_ML); 
vect_mean_ML=[meanxs_ML;meanys_ML;meanrs_ML;meanbear_ML]; 
end

% Calculate Variance = E[(a - mean)^2]
% ----------------------------------------------------- 
varxs_SI=var(bias_Xs_SI(:,1)); 
varys_SI=var(bias_Xs_SI(:,2)); 
varrs_SI=var(bias_Rs_SI); 

varbear_SI=var(bias_bearing_SI);
vect_var_SI=[varxs_SI;varys_SI;varrs_SI;varbear_SI];

%ML
if (bML==1)
    varxs_ML=var(bias_Xs_ML(:,1)); 
    varys_ML=var(bias_Xs_ML(:,2)); 
    varrs_ML=var(bias_Rs_ML); 
    varbear_ML=var(bias_bearing_ML);

    vect_var_ML=[varxs_ML;varys_ML;varrs_ML;varbear_ML]; 
end

% Calculate second moment (RMS)= sqrt {E[a^2]} = sqrt {mean^2 + variance} 
% ----------------------------------------------------- 
rmsxs_SI=sqrt(mean(bias_Xs_SI(:,1)).^2+varxs_SI); 
rmsys_SI=sqrt(mean(bias_Xs_SI(:,2)).^2+varys_SI); 
rmsrs_SI=sqrt(mean(bias_Rs_SI).^2+varrs_SI); 
rmsbear_SI=sqrt(mean(bias_bearing_SI).^2+varbear_SI);

vect_rms_SI=[rmsxs_SI;rmsys_SI;rmsrs_SI;rmsbear_SI];

%ML
if (bML==1) 
    rmsxs_ML=sqrt(mean(bias_Xs_ML(:,1)).^2+varxs_ML); 
    rmsys_ML=sqrt(mean(bias_Xs_ML(:,2)).^2+varys_ML); 
    rmsrs_ML=sqrt(mean(bias_Rs_ML).^2+varrs_ML); 
    rmsbear_ML=sqrt(mean(bias_bearing_ML).^2+varbear_ML);

    vect_rms_ML=[rmsxs_ML;rmsys_ML;rmsrs_ML;rmsbear_ML]; 
end

% Calculate Cramer Rao Bound 
%
cov_mat=Noise_Var.*(0.5*ones(length(d))+0.5*eye(length(d)));

for i=1:length(d)
    a1=[xs_src_actual-locSen(i+1,1) ys_src_actual-locSen(i+1,2)];
    a2=sqrt((xs_src_actual-locSen(i+1,1))^2+(ys_src_actual-locSen(i+1,2))^2);
    b1=[xs_src_actual-locSen(1,1) ys_src_actual-locSen(1,2)];
    b2=sqrt((xs_src_actual-locSen(1,1))^2+(ys_src_actual-locSen(1,2))^2); 
    jacobian(i,:)= (a1/a2)-(b1/b2);
end

fisher=jacobian'*inv(cov_mat)*jacobian;

crlb= trace(fisher^-1); % compare with MSE of Rs

% ----------------------------------------------------- 
% Generate Plots
% -----------------------------------------------------

% hfig1=figure;
if (bML==1)
plot(xi, yi,'bv',Xs_SI(:,1), Xs_SI(:,2),'mo',Xs_ML(:,1), Xs_ML(:,2), 'kd'); % plot both SI and ML
hold on
plot(xs_src_actual, ys_src_actual,'rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',6); % plot both SI and ML

else
plot(xi, yi,'bv', xs_src_actual, ys_src_actual, 'r^', Xs_SI(:,1), Xs_SI(:,2), 'mo'); % plot just SI only
end

title('Sensor and Source Location');
str1=sprintf('[Xs, Ys, Zs, Rs, Bearing], Noise Std = %s*Rs',Noise_Factor); 
str2=sprintf('SI Method');
str3=sprintf('RMS = [%s, %s, %s, %s, %s]', rmsxs_SI, rmsys_SI,rmsrs_SI, rmsbear_SI);
str4=sprintf('Mean = [%s, %s, %s, %s, %s]', meanxs_SI, meanys_SI,meanrs_SI, meanbear_SI);
str5=sprintf('Variance = [%s, %s, %s, %s, %s]', varxs_SI, varys_SI,varrs_SI, varbear_SI);
if (bML==1)
str6=sprintf('ML Method');
str7=sprintf('RMS = [%s, %s, %s, %s, %s]', rmsxs_ML, rmsys_ML,rmsrs_ML, rmsbear_ML);
str8=sprintf('Mean = [%s, %s, %s, %s, %s]', meanxs_ML, meanys_ML, meanrs_ML, meanbear_ML);
str9=sprintf('Variance = [%s, %s, %s, %s, %s]', varxs_ML, varys_ML, varrs_ML, varbear_ML);
str=sprintf('%s \n%s \n%s \n%s \n%s \n%s \n%s \n%s \n%s', str1, str2, str3, str4,str5, str6, str7, str8, str9);
legend('sensor location', 'calculated source location(SI)','calculated source location (ML)','actual source location ' );
else
str=sprintf('%s \n%s \n%s \n%s \n%s \n%s \n%s \n%s \n%s', str1, str2, str3, str4,str5);
legend('sensor location', 'actual source location', 'calculated source location (SI)');
end


xlabel('Distance (metres) in X direction'); 
ylabel('Distance (metres) in Y direction');

% generate results output files 
fid = fopen('results.txt','w');

for k=1:nRun, 
    fprintf(fid,'%e\t%e\t%e\t%e\n',bias_Xs_SI(k,1),bias_Xs_SI(k,2), bias_Rs_SI(k), bias_bearing_SI(k)); 
end
fprintf(fid,'\n%e\t %e\t %e\t %e\t %e\n', meanxs_SI, meanys_SI, meanrs_SI, meanbear_SI);
fprintf(fid,'%e\t %e\t %e\t %e\t %e\n', varxs_SI, varys_SI, varrs_SI, varbear_SI);
fprintf(fid,'%e\t %e\t %e\t %e\t %e\n', rmsxs_SI, rmsys_SI, rmsrs_SI, rmsbear_SI);

fclose(fid);
axis([-0.1,0.35,-0.05,0.5]);

5.仿真演示

 6.本算法写论文思路

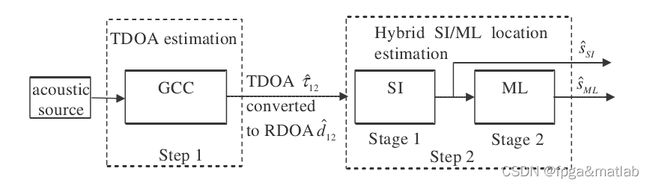
第一部分求时延

      用8个麦克风阵列采集一组正弦波声源信号. 麦克的位置是已知的. 这样对于同一个声源, 不同麦克采集到的信号会有时延. 以其中的一个声源作为参考用GCC-PHAT方法就可以得到七个time delay. 声音传播速度已知就可以得到七个range difference of arrival

第二部分估计声源位置

       用路程差就可以估算声源的位置. 用到两个方法 hybrid spherical interpolation/maximum likelihood (SI/ML) estimation method(应该叫球面散乱数据插值方法/最大似然估计) 然后就可以得到声源坐标, 公式和MATLAB代码文献里都有,

7.参考文献

[1]王丽丽, 徐应祥. 基于散乱数据的球面自然样条插值法[J]. 成都信息工程学院学报, 2012, 27(5):5.

8.相关算法课题及应用

麦克风定位

麦克风阵列

声源定位

A36-04