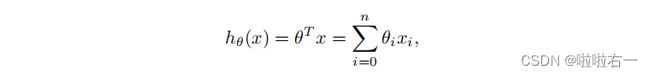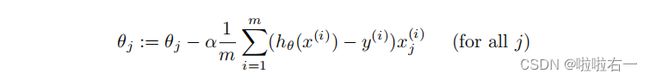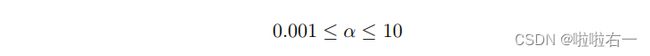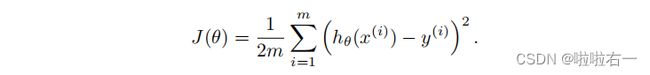机器学习 | 实验二:多变量线性回归
⭐ 对应笔记
单变量线性回归
多变量线性回归
描述
在本练习中,我们将使用梯度下降和正态方程来研究多元线性回归。我们还将研究代价函数J(θ)、梯度下降的收敛性和学习率α之间的关系。
数据
这是俄勒冈州波特兰市的一套房价训练集,其中输出y (i)是价格,投入的x (i)是居住面积和卧室的数量。有m = 47个训练样例。
预处理数据
将训练样例的数据加载到程序中,并将x_0=1截距项添加到x矩阵中。
x=load('ex2x.dat');
y=load('ex2y.dat');
m=length(y);
x=[ones(m,1),x];看看输入值x (i)的值,并注意到居住区域大约是卧室数量的1000倍。这种差异意味着对输入进行预处理将显著提高梯度下降的效率。在您的程序中,根据标准差来衡量这两种类型的输入,并将它们的平均值设为零。
%数据标准化,进行特征收缩,减少迭代次数,加快梯度下降速度
sigma=std(x);
mu=mean(x);
x(:,2)=(x(:,2)−mu(2))./sigma(2);
x(:,3)=(x(:,3)−mu(3))./sigma(3);梯度下降
以前,我们对一个单变量回归问题实现了梯度下降。现在唯一的区别是在矩阵x中还有一个特征。
(1)假设函数依然是
(2)梯度下降规则
同样的,需要将θ初始化为0
使用J(θ)选择一个学习率
现在是时候选择学习率α了。这部分的目标是在如下范围选择一个好的学习率
我们将通过进行初始选择、运行梯度下降和观察成本函数,并相应地调整学习率来做到这一点。回想一下,成本函数被定义为
代价函数也可以写成以下向量化形式
其中
当我们使用像Matlab/Octave这样的数值计算工具时,向量化的版本是非常有用和有效的,而且这两种形式是等价的。
现在,以初始学习速率运行梯度下降大约50次迭代。在每次迭代中,计算J(θ)并将结果存储在一个向量J中。最后一次迭代后,将J值与迭代次数进行绘制。
theta=zeros(size(x(1,:)))'; % initialize fitting parameters
alpha=0.18;
J=zeros(50,1);
for num_iterations=1:50
h=x*theta;%拟合函数
E=h-y;
J(num_iterations,1)=(0.5/m)*(E'*E);
theta=theta-(alpha/m)*x'*E;
end
figure;
plot(0:49,J(1:50),'-')
xlabel('Number of iterations')
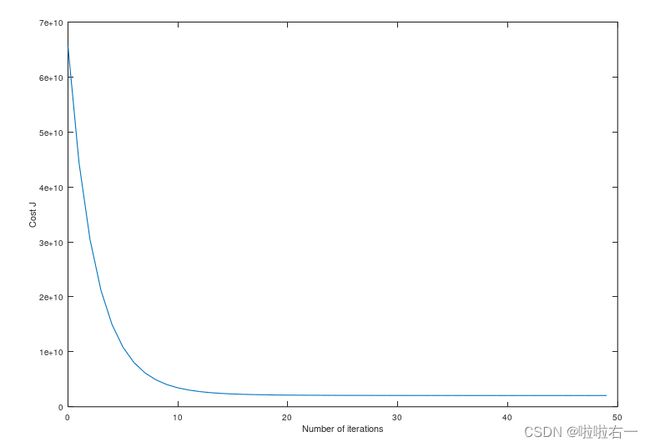
ylabel('Cost J')我这里选用了0.18的学习率,所得图像为:
如果你的图表看起来非常不同,特别是如果你的J(θ)值增加了,甚至失效了, 那么调整学习率,然后再试一次。我们建议以次小值的3倍(即0.01、0.03、0.1、0.3等)测试α。如果这将帮助您看到曲线中的总体趋势,那么您可能还希望调整正在运行的迭代次数。
为了比较不同的学习率如何影响收敛性,在同一图上绘制多个学习率的J(θ)是有帮助的。Matlab/Octave中,这可以通过在图之间保持命令多次执行梯度下降来实现。具体地说,如果您尝试了三个不同的alpha值(您可能应该尝试更多的值),并将成本存储在J1、J2和J3中,您可以使用以下命令在同一图上绘制它们:
plot(0:49,J1(1:50),'b−');
hold on;
plot(0:49,J2(1:50),'r−');
plot(0:49,J3(1:50),'k−');最后的参数'b−','r−','k−'为图表指定了不同的绘图样式。键入help plot以获取有关打印样式的更多信息。
x = load('ex2x.dat');
y = load('ex2y.dat');
m = length(y);
x = [ones(m,1),x];
sigma = std(x);
mu = mean(x);
x(:,2) = (x(: ,2) - mu(2)) ./ sigma(2);
x(:,3) = (x(: ,3) - mu(3)) ./ sigma(3);
theta = zeros(size(x(1,:)))';
alpha = [0.01, 0.03, 0.1, 0.3];
J = zeros(50,1);
for k = 1:4
theta = zeros(size(x(1,:)))';
for num_i = 1:50
J(k,num_i) = (0.5/m) .* (x * theta - y)' * (x * theta - y);
theta = theta - alpha(k) / m * (x' * (x * theta - y));
end
end
figure;
plot(0:49,J(1, 1:50),'b-');
hold on;
plot(0:49,J(2, 1:50),'r-');
plot(0:49,J(3, 1:50),'k-');
plot(0:49,J(4, 1:50),'y-');
xlabel ('Number of iterations')
ylabel ('Cost J ')
legend('alpha=0.01','alpha1=0.03','alpha2=0.1','alpha3=0.3');回答下列问题
⭐随着学习率的变化,观察成本函数的变化。当学习率太小时会发生什么?太大了?
梯度下降算法的每次迭代受到学习率的影响, 如果学习率过小,则达到收敛所需的迭代次数会非常高; 如果学习率过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
⭐使用您找到的最佳学习率,运行梯度下降直到收敛找到
(a)θ 的最终值
(b)1650平方英尺和3间卧室的房屋预计价格。
这里选用0.3作为学习率。
x = load('ex2x.dat');
y = load('ex2y.dat');
m = length(y);
x = [ones(m,1),x];
sigma = std(x);
mu = mean(x);
x(:,2) = (x(: ,2) - mu(2)) ./ sigma(2);
x(:,3) = (x(: ,3) - mu(3)) ./ sigma(3);
theta = zeros(size(x(1,:)))';
alpha = 0.3;
J = zeros(50,1);
for num_i = 1:50
J(num_i,1) = (0.5/m) .* (x * theta - y)' * (x * theta - y);
theta = theta - alpha / m * (x' * (x * theta - y));
end
figure;
plot(0:49,J,'r-');
xlabel ('Number of iterations')
ylabel ('Cost J ')
p = (1650 - mu(2))./sigma(2);
q = (3 - mu(3))./sigma(3);
temp = [1;p;q];
price = theta'*temp;θ 的最终值和最后的预测房价为:
正规方程
使用这个公式不需要任何特征缩放,你将在一次计算中得到一个精确的解:没有像梯度下降一样的“循环直到收敛”
⭐用正规方程计算θ,并计算房价,观察和梯度下降法得到的价格一样吗?
x = load('ex2x.dat'); y = load('ex2y.dat');
m = length(y);
x = [ones(m,1),x];
theta = zeros(size(x(1,:)))';
theta = pinv(x'*x)*x'*y;
temp=[1;1650;3];
price = theta'*temp;最后所求得房价和梯度下降法求得的房价大致相同,仅有些许误差。