联邦学习算法介绍-FedAvg详细案例-Python代码获取
联邦学习算法介绍-FedAvg详细案例-Python代码获取
- 一、联邦学习系统框架
- 二、联邦平均算法(FedAvg)
- 三、联邦随梯度下降算法 (FedSGD)
- 四、差分隐私随联邦梯度下降算法 (DP-FedSGD)
- 五、差分隐私联邦平均算法 (DP-FedAVG)
- 六、FedAVG 案例附代码
-
- 1)案例背景
- 2)参数设置
- 3)结果展示
- 4)代码详解
- 七、完整项目代码获取方式
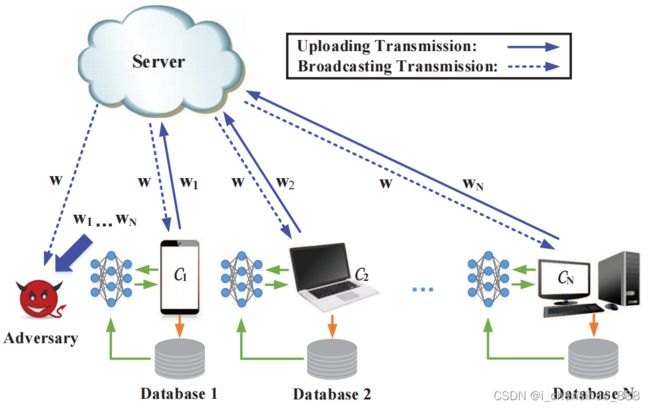
一、联邦学习系统框架
由服务端收集各客户端的梯度信息,通过聚合计算后再分发给各客户端,从而实现多个客户端联合训练模型,且“原始数据不出岛”,从而保护了客户端数据隐私。
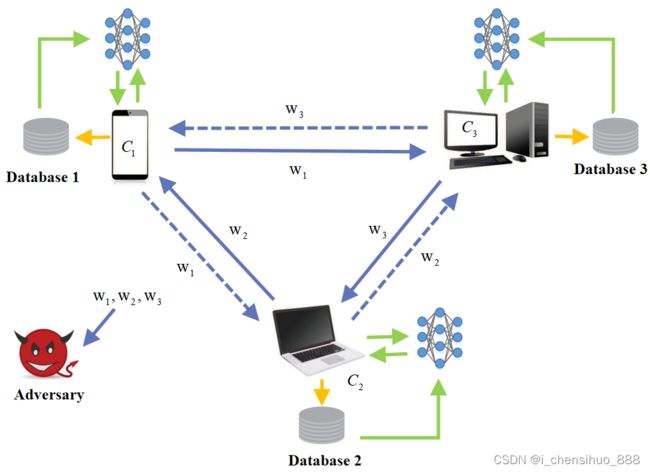
假设中心方是好奇的,那么客户端通过某种规则向其他客户端广播梯度信息,收到梯度信息的客户端聚合参数并训练,将新的梯度信息广播。
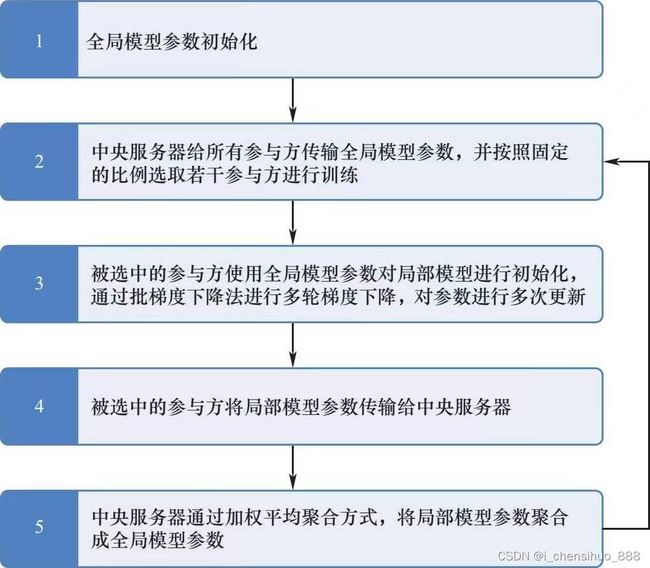
二、联邦平均算法(FedAvg)
输入: 全局模型参数初始值 ω 0 \omega^0 ω0, 参与方个数 n n n, 批样本大小 B B B, 训练轮数 E E E, 参与方比例 C C C, 局部模型学习率 η \eta η, 各参与方的样本个数 m k m_k mk 。
输出: 最后一次迭代的全局模型参数 ω t + 1 \omega_{t+1} ωt+1
1.中央服务器初始化全局模型参数 ω 0 \omega^0 ω0, 并传输给所有参与方。
2.对 t = 0 , 1 , 2 , ⋯ t=0,1,2, \cdots t=0,1,2,⋯, 迭代以下步骤直到全局模型参数 ω t + 1 \omega_{t+1} ωt+1 收敛。
(1) 中央服务器根据参与方比例 C ∈ ( 0 , 1 ] C \in(0,1] C∈(0,1], 计算参与第 t t t 轮迭代的参与方个数:
M ← max ( C × n , 1 ) M \leftarrow \max (C \times n, 1) M←max(C×n,1)
(2) 中央服务器随机选取 M M M 个参与方, 构成参与方集合 S t S_t St
(3) 对 ∀ k ∈ S t \forall k \in S_t ∀k∈St, 通过以下步骤更新局部模型参数:
[1]使用接收到的模型参数 ω t \omega_t ωt 进行模型初始化 ω t + 1 k ⟵ ω t \omega_{t+1}^k \longleftarrow \omega_t ωt+1k⟵ωt 。
[2]将数据索引集 P k P_k Pk 按照批样本大小 B B B 分为若干个批次, 记由这些批次构成的集合为 B k B_k Bk 。 对每次训练 j = 1 , ⋯ , E j=1, \cdots, E j=1,⋯,E, 使用 ∀ b ∈ B k \forall b \in B_k ∀b∈Bk, 更新局部模型参数:
ω t + 1 k ⟵ ω t + 1 k − η ∇ F k ( ω ; b ) \omega_{t+1}^k \longleftarrow \omega_{t+1}^k-\eta \nabla F_k(\omega ; b) ωt+1k⟵ωt+1k−η∇Fk(ω;b)
将更新好的局部模型参数 ω l + 1 k \omega_{l+1}^k ωl+1k 传输给中央服务器。
(4) 中央服务器聚合所有参数,并传输回所有参与方
ω t + 1 = ∑ k = 1 M m k m ω t + 1 k \omega_{t+1}=\sum_{k=1}^M \frac{m_k}{m} \omega_{t+1}^k ωt+1=k=1∑Mmmkωt+1k
m k m \frac{m_k}{m} mmk 为t+1轮聚合中客户端k占参与训练的M个客户端总样本的比例。
三、联邦随梯度下降算法 (FedSGD)
当训练轮数 E = 1 E=1 E=1, 且批样本大小 B B B 是对应的参与方的总样本个数时, FedAvg算法退化为 FedSGD算法。
使用各自的所有样本, 对参数 ω l + 1 k \omega_{l+1}^k ωl+1k 进行一次梯度下降, 计算参数 ω t + 1 k \omega_{t+1}^k ωt+1k 的梯度:
g k = ∇ F k ( ω t + 1 k ) g_k=\nabla F_k\left(\omega_{t+1}^k\right) gk=∇Fk(ωt+1k)
或者计算参数更新值
ω t + 1 k ⟵ ω t + 1 k − η g k \omega_{t+1}^k \longleftarrow \omega_{t+1}^k-\eta g_k ωt+1k⟵ωt+1k−ηgk
其中 η \eta η 是学习率。
四、差分隐私随联邦梯度下降算法 (DP-FedSGD)
1.参数更新量的裁剪方式ClipFn
裁剪方式分2种,即水平裁剪和分层裁剪。
(1) 水平裁剪。记参数更新量矢量为 Δ \Delta Δ, 将其 2 -范数的上界设为 S ∈ R S \in R S∈R, 即:
π ( Δ , S ) = def Δ ⋅ min ( 1 , S ∥ Δ ∥ ) \pi(\boldsymbol{\Delta}, S) \stackrel{\text { def }}{=} \boldsymbol{\Delta} \cdot \min \left(1, \frac{S}{\|\Delta\|}\right) \quad π(Δ,S)= def Δ⋅min(1,∥Δ∥S)
(2)分层裁剪。面向神经网络模型, 假设网络总共有 c c c 层, 每一层的参数更新量矢量分别为 Δ ( 1 ) , ⋯ , Δ ( c ) \Delta(1), \cdots, \Delta(c) Δ(1),⋯,Δ(c), 对应的 2 -范数上界分别为 S 1 , ⋯ S_1, \cdots S1,⋯, S c S_c Sc, 通过水平裁剪的方法, 分别对每一层的矢量进行裁剪:
Δ ′ ( j ) = π ( Δ ( j ) , S j ) \boldsymbol{\Delta}^{\prime}(j)=\pi\left(\boldsymbol{\Delta}(j), S_j\right) Δ′(j)=π(Δ(j),Sj)
总体的参数更新量裁剪上界定义为
S = ∑ j = 1 c S j 2 S=\sqrt{\sum_{j=1}^c S_j^2 } S=j=1∑cSj2
2.中央服务器通过以下步骤对局部模型参数更新量进行聚合:
(1)计算聚合结果
关于加权聚合方式
f ( C ) = ∑ k ∈ C d k Δ k ∑ k ∈ C d k f(C)=\frac{\sum_{k \in C} d_k \Delta^k}{\sum_{k \in C} d_k} f(C)=∑k∈Cdk∑k∈CdkΔk
(其中 Δ k \Delta^k Δk 是参与方 k k k 的参数更新量, C C C为一轮中参与迭代的参与方集合)的有界灵敏度(Bounded-sensitivity)的估计量,分为以下2种:
[1]
f ~ f ( C ) = ∑ k ∈ C d k Δ k q D \tilde{f}_{\mathrm{f}}(C)=\frac{\sum_{k \in C} d_k \Delta^k}{q D} f~f(C)=qD∑k∈CdkΔk
其中 d k = min ( m k m ^ , 1 ) d_k=\min \left(\frac{m_k}{\hat{m}}, 1\right) dk=min(m^mk,1), 是每个参与方的权重; D = ∑ k = 1 n d k D=\sum_{k=1}^n d_k D=∑k=1ndk, q q q为每轮通信中参与方的选择概率。
[2]
f ~ c ( C ) = ∑ k ∈ C d k Δ k max ( q D min , ∑ k ∈ C d k ) \tilde{f}_{\mathrm{c}}(C)=\frac{\sum_{k \in C} d_k \Delta^k}{\max \left(q D_{\text {min }}, \sum_{k \in C} d_k\right)} f~c(C)=max(qDmin ,∑k∈Cdk)∑k∈CdkΔk
其中 D min D_{\text {min }} Dmin 是预先设置的关于权重和的超参数。
(2)令 S ← \leftarrow ← 裁剪方式ClipFn中的裁剪上界, 根据选定的有界灵敏度估计量和噪声规模 z, 设置高斯噪声的方差:
σ ← { z S q D for f ~ f or 2 z S q D min for f ~ c } \sigma \leftarrow\left\{\frac{z S}{q D} \text { for } \tilde{f}_{\mathrm{f}} \text { or } \frac{2 z S}{q D_{\min }} \text { for } \tilde{f}_{\mathrm{c}}\right\} σ←{qDzS for f~f or qDmin2zS for f~c}
(3)聚合全局模型的参数为
ω t + 1 ← ω t + Δ t + 1 + N ( 0 , I σ 2 ) \omega_{t+1} \leftarrow \omega_t+\Delta_{t+1}+N\left(0, I \sigma^2\right) ωt+1←ωt+Δt+1+N(0,Iσ2)
其中, N ( 0 , I σ 2 ) N\left(0, I \sigma^2\right) N(0,Iσ2) 是均值为 0 、方差为 σ 2 \sigma^2 σ2 的高斯分布; I I I 是单位方阵,行数和列数都是参数的个数。
(4)根据 z z z 和 M \mathcal{M} M 计算隐私损失值并输出。
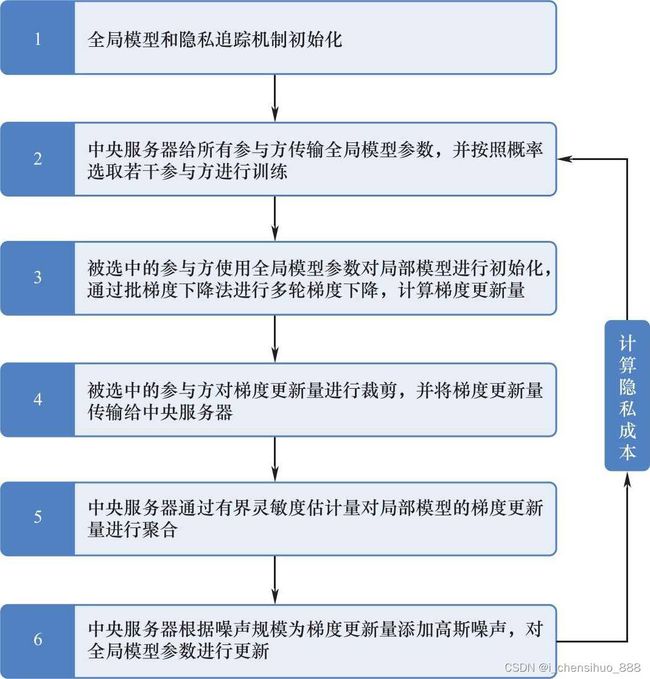
五、差分隐私联邦平均算法 (DP-FedAVG)
在DP-FedSGD中,被选中的参与方使用全局模型参数对局部模型进行初始化,通过批梯度下降法进行多轮梯度下降,计算梯度更新量。而在DP-FedAVG中,是利用一个批次的数据进行一次梯度下降,计算梯度更新量。
六、FedAVG 案例附代码
1)案例背景
收集2012年某10个城市每天每小时的电力数据。用前24时刻的电力负荷值以及该时刻的4个相关气象数据,来预测该时刻的电力负荷值。
构造四层的深度网络:
z 1 = I w 1 , h 1 = σ ( z 1 ) z 2 = h 1 w 2 , h 2 = σ ( z 2 ) z 3 = h 2 w 3 , h 3 = σ ( z 3 ) z 4 = h 3 w 4 , O = σ ( z 4 ) loss = 1 2 ( O − y ) 2 \begin{gathered} z_1=I w_1, h_1=\sigma\left(z_1\right) \\ z_2=h_1 w_2, h_2=\sigma\left(z_2\right) \\ z_3=h_2 w_3, h_3=\sigma\left(z_3\right) \\ z_4=h_3 w_4, O=\sigma\left(z_4\right) \\ \text { loss }=\frac{1}{2}(O-y)^2 \end{gathered} z1=Iw1,h1=σ(z1)z2=h1w2,h2=σ(z2)z3=h2w3,h3=σ(z3)z4=h3w4,O=σ(z4) loss =21(O−y)2
σ \sigma σ为sigmoid激活函数。
2)参数设置
| 参数 | 值 |
|---|---|
| 聚合轮数 | 5 |
| 本地训练次数 | 20 |
| 客户端总数 | 10 |
| 学习率 | 0.08 |
| 本地批量样本大小 | 50 |
| 优化器 | adam |
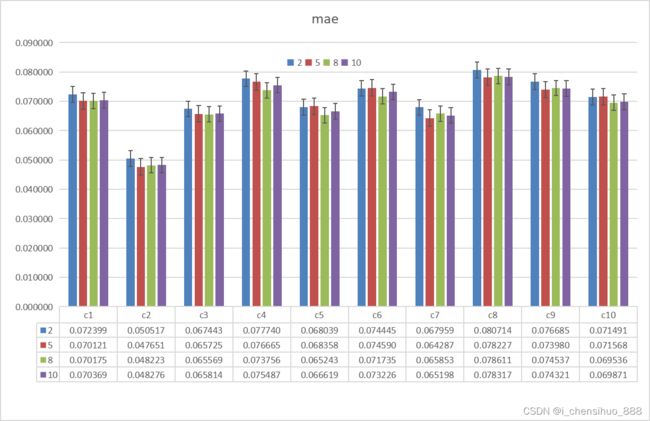
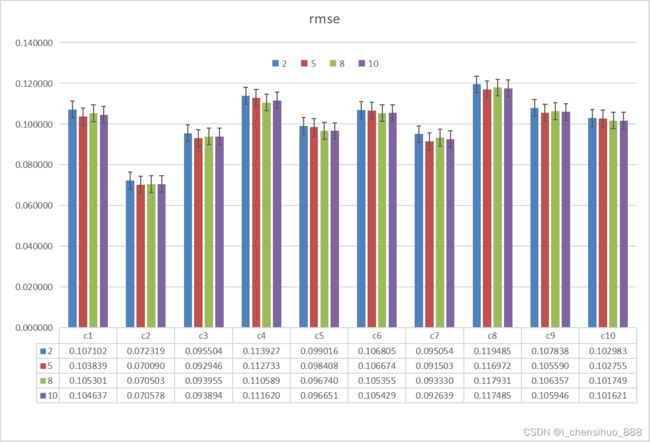
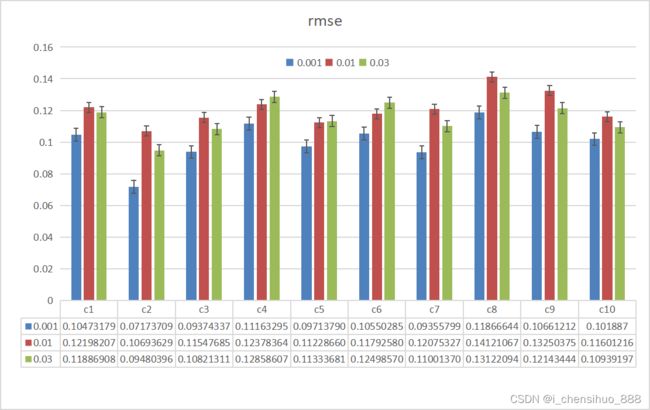
3)结果展示
向梯度中添加随机噪声
4)代码详解
数据结构,在本地文件夹中,有10个csv文件,这10个文件各自代表一个客户端。
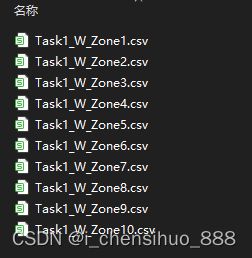
在每个csv文件中,均有7个指标,6577条样本,其中第一列表示服务端id。
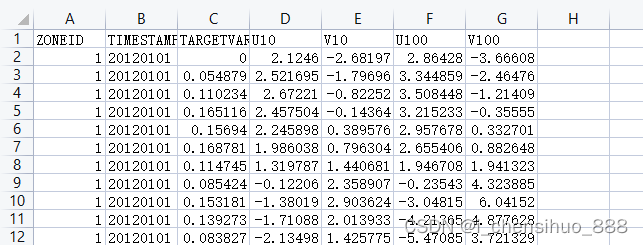
第一步,加载数据。首先需要划分每个客户端的训练集和测试集,本文设置了每个客户端数据结构与样本数量一致(也可以不一致,通过样本对齐方法即可)。
# -*- coding: utf-8 -*-
"""
@File :bp_nn.py
"""
import copy
import sys
import numpy as np
import pandas as pd
from torch import nn
from tqdm import tqdm
sys.path.append('../')
from sklearn.metrics import mean_absolute_error, mean_squared_error
from itertools import chain
from models import BP ##自定义
import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE" #避免jupyter崩溃
clients_wind = ['Task1_W_Zone' + str(i) for i in range(1, 11)]
from args import args_parser ##自定义参数
def load_data(file_name): #读取某一个文件---横向联邦学习
df = pd.read_csv(os.path.dirname(os.getcwd()) + '/data/Wind_new/Task 1/Task1_W_Zone1_10/' + file_name + '.csv', encoding='gbk')
columns = df.columns
df.fillna(df.mean(), inplace=True)
for i in range(3, 7): # 3,4,5,6
MAX = np.max(df[columns[i]])
MIN = np.min(df[columns[i]])
df[columns[i]] = (df[columns[i]] - MIN) / (MAX - MIN) #将3,4,5,6列的值,标准化
return df #0-6列,后4列已经标准化
def nn_seq_wind(file_name, B): #B 实则为本地批量大小
print('data processing...')
dataset = load_data(file_name)
# split
train = dataset[:int(len(dataset) * 0.6)] #前60%为训练集
val = dataset[int(len(dataset) * 0.6):int(len(dataset) * 0.8)] #中间20%为验证集
test = dataset[int(len(dataset) * 0.8):len(dataset)] #最后20%为测试集
def process(data): #将特征与标签分开
columns = data.columns
wind = data[columns[2]]
wind = wind.tolist() #转换成列表 https://vimsky.com/examples/usage/python-pandas-series-tolist.html
data = data.values.tolist()
X, Y = [], []
for i in range(len(data) - 30):
train_seq = []
train_label = []
for j in range(i, i + 24): #24小时
train_seq.append(wind[j])
for c in range(3, 7):
train_seq.append(data[i + 24][c])
train_label.append(wind[i + 24])
X.append(train_seq)
Y.append(train_label)
X, Y = np.array(X), np.array(Y)
length = int(len(X) / B) * B
X, Y = X[:length], Y[:length]
return X, Y
train_x, train_y = process(train)
val_x, val_y = process(val)
test_x, test_y = process(test)
return [train_x, train_y], [val_x, val_y], [test_x, test_y]
def get_val_loss(args, model, val_x, val_y): #验证集,计算损失,model即为nn
batch_size = args.B
batch = int(len(val_x) / batch_size) # 计算循环次数
val_loss = []
for i in range(batch):
start = i * batch_size
end = start + batch_size
model.forward_prop(val_x[start:end], val_y[start:end])
model.backward_prop(val_y[start:end])
val_loss.append(np.mean(model.loss))
return np.mean(val_loss)
def train(args, nn):
print('training...')
tr, val, te = nn_seq_wind(nn.file_name, args.B)
train_x, train_y = tr[0], tr[1]
val_x, val_y = val[0], val[1]
nn.len = len(train_x) # nn.len 训练集的长度
batch_size = args.B # 每批次大小
epochs = args.E # 迭代次数
batch = int(len(train_x) / batch_size) #每一迭代,需要训练多少次
# training
min_epochs = 10
best_model = None
min_val_loss = 5
for epoch in tqdm(range(epochs)):
train_loss = []
for i in range(batch):
start = i * batch_size
end = start + batch_size
nn.forward_prop(train_x[start:end], train_y[start:end])
nn.backward_prop(train_y[start:end])
train_loss.append(np.mean(nn.loss))
# validation
val_loss = get_val_loss(args, nn, val_x, val_y)
if epoch + 1 >= min_epochs and val_loss < min_val_loss:
min_val_loss = val_loss
best_model = copy.deepcopy(nn)
print('epoch {:03d} train_loss {:.8f} val_loss {:.8f}'.format(epoch, np.mean(train_loss), val_loss))
return best_model
def get_mape(x, y):
"""
:param x: true value
:param y: pred value
:return: mape
"""
return np.mean(np.abs((x - y) / x))
def test(args, nn):
tr, val, te = nn_seq_wind(nn.file_name, args.B)
test_x, test_y = te[0], te[1]
pred = []
batch = int(len(test_y) / args.B)
for i in range(batch):
start = i * args.B
end = start + args.B
res = nn.forward_prop(test_x[start:end], test_y[start:end])
res = res.tolist()
res = list(chain.from_iterable(res))
#chain.from_iterable()属于终止迭代器类别 https://blog.csdn.net/qq_42708830/article/details/106731144
# print('res=', res)
pred.extend(res)
pred = np.array(pred)
print('mae:', mean_absolute_error(test_y.flatten(), pred), 'rmse:',
np.sqrt(mean_squared_error(test_y.flatten(), pred)))
def main():
args = args_parser()
for client in clients_wind:
nn = BP(args, client)
nn = train(args, nn)
test(args, nn)
if __name__ == '__main__':
main()
第二步,建立模型。在这里,前向传播计算结果,后向传播更新梯度。
# -*- coding:utf-8 -*-
"""
@File: models.py
"""
import numpy as np
from torch import nn
class BP:
def __init__(self, args, file_name):
self.file_name = file_name
self.len = 0
self.args = args
self.input = np.zeros((args.B, args.input_dim)) # self.B samples per round (本地批量大小=50,输入维度=28)
self.w1 = 2 * np.random.random((args.input_dim, 20)) - 1 # limit to (-1, 1) (28,20)
self.z1 = 2 * np.random.random((args.B, 20)) - 1 #np.random.random生成args.B=50行 20列的0-1浮点数;*2→(0-2),再-1,变成(-1,1)
self.hidden_layer_1 = np.zeros((args.B, 20)) #(50,20)
self.w2 = 2 * np.random.random((20, 20)) - 1 #(20,20)
self.z2 = 2 * np.random.random((args.B, 20)) - 1 #(50,20)
self.hidden_layer_2 = np.zeros((args.B, 20)) #(50,20)
self.w3 = 2 * np.random.random((20, 20)) - 1 #(20,20)
self.z3 = 2 * np.random.random((args.B, 20)) - 1 #(50,20)
self.hidden_layer_3 = np.zeros((args.B, 20)) #(50,20)
self.w4 = 2 * np.random.random((20, 1)) - 1 #(20,1)
self.z4 = 2 * np.random.random((args.B, 1)) - 1 #(50,1)
self.output_layer = np.zeros((args.B, 1)) #(50,1)
self.loss = np.zeros((args.B, 1)) #(50,1)
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def sigmoid_deri(self, x):
return x * (1 - x)
def forward_prop(self, data, label):
self.input = data
# self.input(50,28) self.w1(28, 20) self.z1(50, 20)
self.z1 = np.dot(self.input, self.w1) # np.dot 计算过程就是将向量中对应元素相乘,再相加所得。即普通的向量乘法运算。
self.hidden_layer_1 = self.sigmoid(self.z1) # self.hidden_layer_1(50, 20)
self.z2 = np.dot(self.hidden_layer_1, self.w2) #self.w2(20,20) self.z2(50, 20)
self.hidden_layer_2 = self.sigmoid(self.z2) # self.hidden_layer_2(50, 20)
self.z3 = np.dot(self.hidden_layer_2, self.w3) #self.w3(20,20) self.z3(50, 20)
self.hidden_layer_3 = self.sigmoid(self.z3) #(50,20)
self.z4 = np.dot(self.hidden_layer_3, self.w4) #self.w4 (20,1) self.z4(50,1)
self.output_layer = self.sigmoid(self.z4) #self.output_layer(50,1)
# error
self.loss = 1 / 2 * (label - self.output_layer) ** 2 ##(50,1) why 1/2 ?
return self.output_layer
def backward_prop(self, label):
# w4
l_deri_out = self.output_layer - label
l_deri_z4 = l_deri_out * self.sigmoid_deri(self.output_layer)
l_deri_w4 = np.dot(self.hidden_layer_3.T, l_deri_z4)
# w3
l_deri_h3 = np.dot(l_deri_z4, self.w4.T)
l_deri_z3 = l_deri_h3 * self.sigmoid_deri(self.hidden_layer_3)
l_deri_w3 = np.dot(self.hidden_layer_2.T, l_deri_z3)
# w2
l_deri_h2 = np.dot(l_deri_z3, self.w3.T)
l_deri_z2 = l_deri_h2 * self.sigmoid_deri(self.hidden_layer_2)
l_deri_w2 = np.dot(self.hidden_layer_1.T, l_deri_z2)
# w1
l_deri_h1 = np.dot(l_deri_z2, self.w2.T)
l_deri_z1 = l_deri_h1 * self.sigmoid_deri(self.hidden_layer_1)
l_deri_w1 = np.dot(self.input.T, l_deri_z1)
# update
self.w4 -= self.args.lr * l_deri_w4 # self.args.lr 学习率=0.08 实则梯度下降
self.w3 -= self.args.lr * l_deri_w3
self.w2 -= self.args.lr * l_deri_w2
self.w1 -= self.args.lr * l_deri_w1
第三步,设置参数。在实例化训练之前,为了便于调参,可将所有参数放在一个单独的文件中。
# -*- coding:utf-8 -*-
"""
@File: args.py
"""
# argparse的用法见csdn的收藏夹,或者https://blog.csdn.net/qq_41762249/article/details/122244624
# --E 相当于关键词参数,如果没有--直接是E,就是位置参数
# type=int 传入参数的类型
# default=20 当没有参数传入时,默认值为20, help='***' 表示对该参数的解释为***
'''
number of rounds of training: 训练次数
number of communication rounds:通信回合数,即上传下载模型次数。
number of total clients:客户端总数
input dimension :输入维度
learning rate :学习率
sampling rate :采样率
local batch size : 本地批量大小
type of optimizer : 优化器类型
--device:有GPU就用,不然就用CPU
weight_decay :权值衰减
weight decay(权值衰减)的使用既不是为了提高你所说的收敛精确度也不是为了提高收敛速度,其最终目的是防止过拟合。在损失函数中,weight decay是放在正则项(regularization)前面的一个系数,正则项一般指示模型的复杂度,所以weight decay的作用是调节模型复杂度对损失函数的影响,若weight decay很大,则复杂的模型损失函数的值也就大。https://blog.csdn.net/xuxiatian/article/details/72771609
step size: 步长
gamma: 伽马参数
--clients: 10个客户端 Task1_W_Zone1、Task1_W_Zone2、Task1_W_Zone3...Task1_W_Zone10
'''
import argparse
import torch
def args_parser():
parser = argparse.ArgumentParser() # 可选参数: description='描述程序内容' 通过命令行 python **.py--help 调用出
parser.add_argument('--E', type=int, default=20, help='number of rounds of training')
parser.add_argument('--r', type=int, default=5, help='number of communication rounds')
parser.add_argument('--K', type=int, default=10, help='number of total clients')
parser.add_argument('--input_dim', type=int, default=28, help='input dimension')
parser.add_argument('--lr', type=float, default=0.08, help='learning rate')
parser.add_argument('--C', type=float, default=0.8, help='sampling rate')
parser.add_argument('--B', type=int, default=50, help='local batch size')
parser.add_argument('--optimizer', type=str, default='adam', help='type of optimizer')
parser.add_argument('--device', default=torch.device("cuda" if torch.cuda.is_available() else "cpu"))
parser.add_argument('--weight_decay', type=float, default=1e-4, help='weight_decay')
parser.add_argument('--step_size', type=int, default=10, help='step size')
parser.add_argument('--gamma', type=float, default=0.1, help='gamma')
clients = ['Task1_W_Zone' + str(i) for i in range(1, 11)]
parser.add_argument('--clients', default=clients)
# args = parser.parse_args()
# args,unknow = parser.parse_known_args()
args = parser.parse_known_args()[0]
return args
第4步,模型训练。
import numpy as np
import random
import copy
import sys
sys.path.append('../')
from algorithms.bp_nn import train, test
from models import BP
from args import args_parser # 一些传入参数,见args.py
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 只看error
#-----------------tf用于设置随机数
import tensorflow as tf
clients_wind = ['Task1_W_Zone' + str(i) for i in range(1, 11)]
# Implementation for FedAvg by numpy. 通过numpy实现FedAvg。
class FedAvg:
def __init__(self, args): #self 默认必须参数,有类中全局变量之效,args表示,调用FedAvg时,必须传入的参数
self.args = args
self.clients = args.clients
self.nn = BP(args=args, file_name='server') # BP是models中的一个类,同样需要传入参数。file_name方便后面为每个客户端取名
self.nns = []
# distribution
for i in range(self.args.K): #args.K,客户端总数; 子程序为每一个客户端构造了一个BP类
#copy.deepcopy() 深复制的用法是将某个变量的值赋给另一个变量(此时两个变量地址不同),因为地址不同,所以变量间互不干扰
s = copy.deepcopy(self.nn)
s.file_name = self.clients[i]
self.nns.append(s)
def server(self):
for t in range(self.args.r): #通信回合数,即本地模型上传下载全局模型次数
print('round', t + 1, ':') # 输出:round1、round2、round3、round4、round5
# m = np.max([int(self.args.C * self.args.K), 1]) # 抽样率*客户端总数,即每一轮参与训练的客户端数量,至少有1个客户端参与
m = 5
print(m)
# sampling
index = random.sample(range(0, self.args.K), m) #在0-(k-1)之间共k个中抽取m个序号,注意是序号/索引
print(len(index))
# dispatch
self.dispatch(index) # 下面定义了dispatch函数:抽中的m本地客户端从服务端下载4个参数
# local updating
self.client_update(index) # 下面定义了client_update函数:抽中的m个客户端进行本地训练
# aggregation
self.aggregation(index) # 下面定义了aggregation函数:抽中的m个客户端,上传本地训练结果参数
# return global model
return self.nn #返回最终聚合后的模型
def aggregation(self, index):
# update w
s = 0 #用来计一轮抽中的m个本地客户端总的样本数
for j in index:
# normal
s += self.nns[j].len
w1 = np.zeros_like(self.nn.w1) #np.zeros_like:生成和self.nn.w1一样的零阵,下同
w2 = np.zeros_like(self.nn.w2)
w3 = np.zeros_like(self.nn.w3)
w4 = np.zeros_like(self.nn.w4)
#-----------------自增1018
nois = 0.05
for j in index: # 对上传的每一个本地模型进行权重的加权求和,权重为该客户端样本数/该轮中参与训练的总样本数
# normal
w1 += self.nns[j].w1 * (self.nns[j].len / s) + tf.random.normal([1],mean=0, stddev=nois).numpy()
w2 += self.nns[j].w2 * (self.nns[j].len / s) + tf.random.normal([1],mean=0, stddev=nois).numpy()
w3 += self.nns[j].w3 * (self.nns[j].len / s) + tf.random.normal([1],mean=0, stddev=nois).numpy()
w4 += self.nns[j].w4 * (self.nns[j].len / s) + tf.random.normal([1],mean=0, stddev=nois).numpy()
# update server 更新服务端参数
self.nn.w1, self.nn.w2, self.nn.w3, self.nn.w4 = w1, w2, w3, w4
def dispatch(self, index):
# distribute
for i in index:
self.nns[i].w1, self.nns[i].w2, self.nns[i].w3, self.nns[i].w4 = self.nn.w1, self.nn.w2, self.nn.w3, self.nn.w4
def client_update(self, index): # update nn
for k in index:
self.nns[k] = train(self.args, self.nns[k])
def global_test(self):
model = self.nn #最终聚合后的模型
c = clients_wind # 10个客户端名称 Task1_W_Zone1、Task1_W_Zone2、Task1_W_Zone3...Task1_W_Zone10
for client in c:
print(client)
model.file_name = client
test(self.args, model)
'''
L1损失函数: mae
均方根误差: rmse
https://blog.csdn.net/qq_45758854/article/details/125807544
'''
def main():
args = args_parser()
fed = FedAvg(args)
fed.server()
fed.global_test()
if __name__ == '__main__':
main()
代码到此结束,以下是运行结果情况。
每次计算时,会输出结果,例如训练数据时情况
training...
data processing...
0%| | 0/20 [00:00<?, ?it/s]epoch 000 train_loss 0.00486654 val_loss 0.00703024
50%|█████ | 10/20 [00:00<00:00, 95.47it/s]epoch 001 train_loss 0.00476797 val_loss 0.00696587
epoch 002 train_loss 0.00470252 val_loss 0.00693571
epoch 003 train_loss 0.00466028 val_loss 0.00693080
epoch 004 train_loss 0.00463130 val_loss 0.00694067
epoch 005 train_loss 0.00460982 val_loss 0.00695734
epoch 006 train_loss 0.00459274 val_loss 0.00697600
epoch 007 train_loss 0.00457843 val_loss 0.00699407
epoch 008 train_loss 0.00456600 val_loss 0.00701034
epoch 009 train_loss 0.00455495 val_loss 0.00702437
epoch 010 train_loss 0.00454502 val_loss 0.00703613
epoch 011 train_loss 0.00453605 val_loss 0.00704578
epoch 012 train_loss 0.00452794 val_loss 0.00705359
epoch 013 train_loss 0.00452062 val_loss 0.00705982
epoch 014 train_loss 0.00451403 val_loss 0.00706475
epoch 015 train_loss 0.00450812 val_loss 0.00706860
epoch 016 train_loss 0.00450283 val_loss 0.00707159
epoch 017 train_loss 0.00449813 val_loss 0.00707389
epoch 018 train_loss 0.00449396 val_loss 0.00707564
...
epoch 019 train_loss 0.00449026 val_loss 0.00707696
Task1_W_Zone1
data processing...
mae: 0.20787641855647404 rmse: 0.2836560807251283
Task1_W_Zone2
data processing...
mae: 0.1631928286850088 rmse: 0.21530131283252676
Task1_W_Zone3
data processing...
测试数据时,会输出每个客户端预测结果,例如
Task1_W_Zone10
data processing...
mae: 0.25128443075937873 rmse: 0.31826369651645525
最后收集这些结果,并可视化。
欢迎评论区交流沟通,博主将定期回复。
七、完整项目代码获取方式
以下方法,任一均可:
(1)点击 GitHub-numpy-FedAvg 自行下载。(访问: https://github.com/chenyiadam/FedAVG.git )
(2)私信留言、评论你的邮箱,我将定期回复。