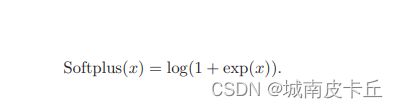第一章---Pytorch快速入门---第二节---自动微分、torch.nn模块

目录

一、pytorch中的自动微分

 二、torch.nn模块

2.1 卷积层

2.2 池化层

2.3 激活函数

 2.4 循环层

 2.5 全连接层

---

一、pytorch中的自动微分

在pytorch中的autograd模块提供了实现任意标量值函数自动求导的类和函数。针对一个张量只需要设置参数requires_grad=True，即可输出其在传播过程中的导数信息。下面通过一个例子来学习pytorch中的自动微分

x=torch.tensor([[1.0,2.0],[3.0,4.0]],requires_grad=True)
y=torch.sum(x**2+2*x+1)
print(x)
print(x**2+2*x+1)
print(y)
print(x.requires_grad)
print(y.requires_grad)
print("--------")
y.backward()
print(x.grad)
"""
上面的程序首先生成一个矩阵x，并指定其可以求导，
然后根据公司y=x**2+2*x+1计算标量y，因为x可以
求导故y也可以求导。然后通过y.backward()自动
计算y在x上的每个元素上的导数，然后通过x的gard
属性即可获取此时x的梯度信息，并且得到的梯度值为2x+2
"""

 二、torch.nn模块

该模块封装了卷积层、池化层、激活函数、循环层、全连接层，通过该模块，我们可以很轻松地构建起一个神经网络。

2.1 卷积层

卷积可以看做是输入和卷积核之间的内积运算，在卷积运算中，通常使用卷积核将输入数据进行卷积运算得到输出作为特征映射，每个卷积核可获得一个特征映射。针对二维图像使用2*2的卷积核，步长为1的运算过程如图所示

 通过上面的卷积运算示例可以发现，卷积操作将周围几个像素的取值经过计算得到一个像素值。使用卷积运算有三个好处：卷积稀疏连接、参数共享、等变表示。

在卷积神经网络中，通过输入卷积核来进行卷积操作，使得输入单元（图像或特征映射）和输出单元（特征映射）之间的连接是稀疏的，这样能够减少需要训练参数的数量，从而加快网络的计算速度。

卷积操作的参数共享特点，主要体现在模型中同一组参数可以被多个函数或操作共同使用。在卷积神经网络中，针对不同的输入会利用同样的卷积核来获得相应的输出。这种参数共享的特点是只需要训练一个参数集，而不需要对每个位置学习一个参数集合。由于卷积核尺寸远远小于输入尺寸，即减少需要学习的参数的数量，并且针对每个卷积层可以使用多个卷积核获取输入的特征映射，对数据具有很强的特征提取和表示能力，并且在卷积运算之后，使得卷积神经网络结构对输入的图像具有平移不变的性质。

在pytorch中针对卷积操作的对象和使用场景不同，有一维卷积、二维卷积、三维卷积与转置卷积。常用的卷积操作对应的类如下：

类	功能作用
torch.nn.Conv1d()	针对输入信号上应用1D卷积
torch.nn.Conv2d()	针对输入信号上应用2D卷积
torch.nn.Conv3d()	针对输入信号上应用3D卷积
torch.nn.ConvTranspose1d()	在输入信号上应用1D转置卷积
torch.nn.ConvTranspose2d()	在输入信号上应用2D转置卷积
torch.nn.ConvTranspose3d()	在输入信号上应用3D转置卷积

torch.nn.Conv2d(in_channels,
                out_channels,
                kernel_size,
                stride,
                padding,
                dilation,
                groups,
                bias=True)
"""
主要参数说明：
in_channels:(整数)输入图像的通道数
out_channels:(整数)经过卷积运算后，输出特征映射的数量
kernel_size:(整数或者元组)卷积核的大小
stride:(整数或者元组，正数)卷积的步长，默认为1
padding:(整数或者元组，正数)在输入两边进行0填充的数量，默认为0
dilation:(整数或者元组、正数)卷积核元素之间的步幅，该参数可调整空洞卷积的空洞大小，默认为1
groups:(整数，正数)从输入通道到输出通道的阻塞连接数
bias:(布尔值，正数)如果bias=True,则添加偏置，默认为True
"""

 下面我们使用一张图像让它经过二维卷积，看看输出后这张图像会是什么样子的。

这是原图

 

from PIL import Image
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
img=Image.open("C:\\Users\\zex\\Pictures\\Img512x512.png")
imgArray=np.array(img.convert("L"),dtype=np.float32)
print("imgArray大小:",imgArray.shape)
plt.figure(figsize=(6,6))
plt.imshow(imgArray,cmap=plt.cm.gray)
plt.axis("off")
plt.show()

上面的代码，使用Image.open()函数读取了图像数据，并且使用convert()方法将其转化为灰度图像，得到了512*512的灰度图像，最后使用plt.imshow(）将其可视化，结果如下图所示

下面我们对该灰度图像进行2D卷积操作，并将卷积处理的图片可视化 

from PIL import Image
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
img=Image.open("C:\\Users\\zex\\Pictures\\Img512x512.png")
imgArray=np.array(img.convert("L"),dtype=np.float32)
print("imgArray大小:",imgArray.shape)
# plt.figure(figsize=(6,6))
# plt.imshow(imgArray,cmap=plt.cm.gray)
# plt.axis("off")
# plt.show()
"""经过上述操作，得到一个512*512的数组，在使用pytorch进行卷积操作之前
 需要将其转化为1*1*512*512的张量
"""
imh,imw=imgArray.shape
imgTensor=torch.from_numpy(imgArray.reshape(1,1,imh,imw))
"""
卷积时需要将图像转化为四维来表示[batch,channel,h,w]
对图像进行卷积操作之后得到两个特征映射
第一个特征映射使用图像轮廓提取卷积核获取
第二个特征映射使用的卷积核为随机数，卷积核尺寸为5*5，对图像的边缘不使用0填充
所以卷积后输出特征映射的尺寸为508*508
"""
#对灰度图像进行卷积提取图像轮廓
kersize=5 #定义边缘检测卷积核，并将维度处理为1*1*5*5
ker=torch.ones(kersize,kersize,dtype=torch.float32)*-1
ker[2,2]=24
ker=ker.reshape(1,1,kersize,kersize)
#进行卷积操作
conv2d=nn.Conv2d(1,2,(kersize,kersize),bias=False)
#设置卷积时使用的核
conv2d.weight.data[0]=ker
#对灰度图像进行卷积操作
imconv2d_out=conv2d(imgTensor)
imconv2d_out_im=imconv2d_out.data.squeeze()
print("卷积后的尺寸",imconv2d_out.shape)
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.imshow(imconv2d_out_im[0],cmap=plt.cm.gray)
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(imconv2d_out_im[1],cmap=plt.cm.gray)
plt.axis("off")
plt.show()

 

 从上图可以看出，使用的边缘特征提取卷积核很好的提取出了图像的边缘信息，而右边的图像使用的卷积核为随机数，得到的卷积结果与原始图像很相似。

2.2 池化层

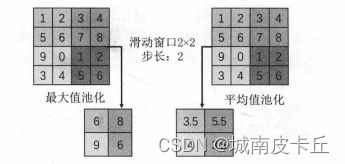
池化操作的一个重要的目的就是对卷积后得到的特征进行进一步的处理（主要降维），池化层可以起到对数据进一步浓缩的效果，从而缓解计算时内存的压力。池化会选取一定大小的区域，如果使用最大值代替则称为最大值池化，如果使用平均值代替则称为平均值池化。两种池化的区别如下图所示

在pytorch中提供了许多池化的类，具体如下表所示：

层对应的类	功能
torch.nn.MaxPool1d()	针对输入信号上应用1D最大值池化
torch.nn.MaxPool2d()	针对输入信号上应用2D最大值池化
torch.nn.MaxPool3d()	针对输入信号上应用3D最大值池化
torch.nn.MaxUnPool1d()	1D最大值池化的部分逆运算
torch.nn.MaxUnPool2d()	2D最大值池化的部分逆运算
torch.nn.MaxUnPool3d()	3D最大值池化的部分逆运算
torch.nn.AvgPool1d()	针对输入信号上应用1D平均值池化
torch.nn.AvgPool2d()	针对输入信号上应用2D平均值池化
torch.nn.AvgPool3d()	针对输入信号上应用3D平均值池化
torch.nn.AdaptiveMaxPool1d()	针对输入信号上应用1D自适应最大值池化
torch.nn.AdaptiveMaxPool2d()	针对输入信号上应用2D自适应最大值池化
torch.nn.AdaptiveMaxPool3d()	针对输入信号上应用3D自适应最大值池化
torch.nn.AdptiveAvgPool1d()	针对输入信号上应用1D自适应平均值池化
torch.nn.AdptiveAvgPool2d()	针对输入信号上应用2D自适应平均值池化
torch.nn.AdptiveAvgPool3d()	针对输入信号上应用3D自适应平均值池化

对于torch.nn.MaxPool2d（）池化操作相关参数的应用，其使用方法如下：

torch.nn.MaxPool2d(kernel_size,
                   stride,
                   padding,
                   dilation,
                   return_indices=False,
                   ceil_mode=False,
)

参数使用说明：

kernei_size:(整数或者数组)最大值池化的窗口大小

strdie:(整数或者数组，正数)最大值池化窗口移动的步长，默认值是kernel_size

padding(整数或者数组，正数)输入的每一条边补充0的层数

dilation:(整数或者数组，正数)一个控制窗口中元素步幅的参数

return_indices:如果为True，则会返回输出最大值得索引，这样就会更加便于之后的torch.nn.MaxUnPool2d操作。

ceil_mode:如果等于True,计算输出信号大小的时候，会使用向上取整，默认是向下取整。

 我们继续拓展上面的一个例子，在上面的例子中，我们对灰度图像进行卷积操作之后，直接进行了卷积结果维度压缩，然后可视化。我们现在在卷积层后面加入池化层，对卷积后的结果进行池化，然后对池化结果进行维度压缩，最后可视化。

首先我们使用最大值池化

from PIL import Image
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
img=Image.open("C:\\Users\\zex\\Pictures\\Img512x512.png")
imgArray=np.array(img.convert("L"),dtype=np.float32)
print("imgArray大小:",imgArray.shape)
"""经过上述操作，得到一个512*512的数组，在使用pytorch进行卷积操作之前
 需要将其转化为1*1*512*512的张量
"""
imh,imw=imgArray.shape
imgTensor=torch.from_numpy(imgArray.reshape(1,1,imh,imw))
"""
卷积时需要将图像转化为四维来表示[batch,channel,h,w]
对图像进行卷积操作之后得到两个特征映射
第一个特征映射使用图像轮廓提取卷积核获取
第二个特征映射使用的卷积核为随机数，卷积核尺寸为5*5，对图像的边缘不使用0填充
所以卷积后输出特征映射的尺寸为508*508
"""
#对灰度图像进行卷积提取图像轮廓
kersize=5 #定义边缘检测卷积核，并将维度处理为1*1*5*5
ker=torch.ones(kersize,kersize,dtype=torch.float32)*-1
ker[2,2]=24
ker=ker.reshape(1,1,kersize,kersize)
#进行卷积操作
conv2d=nn.Conv2d(1,2,(kersize,kersize),bias=False)
#设置卷积时使用的核
conv2d.weight.data[0]=ker
#对灰度图像进行卷积操作
imconv2d_out=conv2d(imgTensor)
#imconv2d_out_im=imconv2d_out.data.squeeze()
print("卷积后的尺寸",imconv2d_out.shape)
#对卷积后的结果进行最大值池化
maxpool2=nn.MaxPool2d(2,stride=2)
pool2_out=maxpool2(imconv2d_out)
#对池化后的输出进行维度压缩
pool2_out_im=pool2_out.squeeze()
print("池化后的尺寸：",pool2_out.shape)
#可视化池化后的图像
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.imshow(pool2_out_im[0].data,cmap=plt.cm.gray)
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(pool2_out_im[1].data,cmap=plt.cm.gray)
plt.axis("off")
plt.show()

 

通过加入窗口为2*2，步长为2的最大值池化层，卷积后输出的特征映射尺寸由508*508变化为254*254。

接下来使用nn.AvgPool2d()函数，对卷积后输出进行平均值池化，并对其进行可视化。

from PIL import Image
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
img=Image.open("C:\\Users\\zex\\Pictures\\Img512x512.png")
imgArray=np.array(img.convert("L"),dtype=np.float32)
print("imgArray大小:",imgArray.shape)
"""经过上述操作，得到一个512*512的数组，在使用pytorch进行卷积操作之前
 需要将其转化为1*1*512*512的张量
"""
imh,imw=imgArray.shape
imgTensor=torch.from_numpy(imgArray.reshape(1,1,imh,imw))
"""
卷积时需要将图像转化为四维来表示[batch,channel,h,w]
对图像进行卷积操作之后得到两个特征映射
第一个特征映射使用图像轮廓提取卷积核获取
第二个特征映射使用的卷积核为随机数，卷积核尺寸为5*5，对图像的边缘不使用0填充
所以卷积后输出特征映射的尺寸为508*508
"""
#对灰度图像进行卷积提取图像轮廓
kersize=5 #定义边缘检测卷积核，并将维度处理为1*1*5*5
ker=torch.ones(kersize,kersize,dtype=torch.float32)*-1
ker[2,2]=24
ker=ker.reshape(1,1,kersize,kersize)
#进行卷积操作
conv2d=nn.Conv2d(1,2,(kersize,kersize),bias=False)
#设置卷积时使用的核
conv2d.weight.data[0]=ker
#对灰度图像进行卷积操作
imconv2d_out=conv2d(imgTensor)
#imconv2d_out_im=imconv2d_out.data.squeeze()
print("卷积后的尺寸",imconv2d_out.shape)
#对卷积后的结果进行最大值池化
# maxpool2=nn.MaxPool2d(2,stride=2)
# pool2_out=maxpool2(imconv2d_out)
avgpool2=nn.AvgPool2d(2,stride=2)
pool2_out=avgpool2(imconv2d_out)
#对池化后的输出进行维度压缩
pool2_out_im=pool2_out.squeeze()
print("池化后的尺寸：",pool2_out.shape)
#可视化池化后的图像
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.imshow(pool2_out_im[0].data,cmap=plt.cm.gray)
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(pool2_out_im[1].data,cmap=plt.cm.gray)
plt.axis("off")
plt.show()

 接下来我们再使用nn.AdaptiveAvgPool2d()函数，对卷积后的输出进行自适应平均值池化并可视化，在使用该函数时，可以使用output_size参数指定输出特征映射的尺寸

from PIL import Image
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
img=Image.open("C:\\Users\\zex\\Pictures\\Img512x512.png")
imgArray=np.array(img.convert("L"),dtype=np.float32)
print("imgArray大小:",imgArray.shape)
"""经过上述操作，得到一个512*512的数组，在使用pytorch进行卷积操作之前
 需要将其转化为1*1*512*512的张量
"""
imh,imw=imgArray.shape
imgTensor=torch.from_numpy(imgArray.reshape(1,1,imh,imw))
"""
卷积时需要将图像转化为四维来表示[batch,channel,h,w]
对图像进行卷积操作之后得到两个特征映射
第一个特征映射使用图像轮廓提取卷积核获取
第二个特征映射使用的卷积核为随机数，卷积核尺寸为5*5，对图像的边缘不使用0填充
所以卷积后输出特征映射的尺寸为508*508
"""
#对灰度图像进行卷积提取图像轮廓
kersize=5 #定义边缘检测卷积核，并将维度处理为1*1*5*5
ker=torch.ones(kersize,kersize,dtype=torch.float32)*-1
ker[2,2]=24
ker=ker.reshape(1,1,kersize,kersize)
#进行卷积操作
conv2d=nn.Conv2d(1,2,(kersize,kersize),bias=False)
#设置卷积时使用的核
conv2d.weight.data[0]=ker
#对灰度图像进行卷积操作
imconv2d_out=conv2d(imgTensor)
#imconv2d_out_im=imconv2d_out.data.squeeze()
print("卷积后的尺寸",imconv2d_out.shape)
#对卷积后的结果进行最大值池化
# maxpool2=nn.MaxPool2d(2,stride=2)
# pool2_out=maxpool2(imconv2d_out)
# avgpool2=nn.AvgPool2d(2,stride=2)
# pool2_out=avgpool2(imconv2d_out)
AdaAvgpool2=nn.AdaptiveAvgPool2d(output_size=(100,100))
pool2_out=AdaAvgpool2(imconv2d_out)
#对池化后的输出进行维度压缩
pool2_out_im=pool2_out.squeeze()
print("池化后的尺寸：",pool2_out.shape)
#可视化池化后的图像
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.imshow(pool2_out_im[0].data,cmap=plt.cm.gray)
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(pool2_out_im[1].data,cmap=plt.cm.gray)
plt.axis("off")
plt.show()

有上图可以看出，经过自适应平均值池化后，特征映射尺寸变小，图像变得更加模糊。

2.3 激活函数

在pytorch中提供了十几种激活函数层所对应的类。

层对应的类	功能
torch.nn.Sigmoid	Sigmoid激活函数
torch.nn.Tanh	Tanh激活函数
torch.nn.ReLU	ReLU激活函数
torch.nn.Softplus	ReLU激活函数的平滑近似

torch.nn.Sigmoid（）对应的Sigmoid激活函数也叫logistic激活函数，计算公式为

 

 从函数图像可以看出，Sigmoid激活函数值域在（0,1）这个开区间内。该函数在神经网络早期也是很常用的激活函数之一，但是当输入远离坐标原点时，函数的梯度就变得很小，几乎为0，所以会影响参数的更新速度。

 torch.nn.Tanh()对应的双曲正切函数，计算公式为：

 由上面的函数图像可以看出，该函数的输出区间是（-1,1），整个函数是以0为中心，虽然Tanh函数曲线和Sigmoid函数的曲线形状比较相近，在输入很大或者很小时，梯度很小，不利于权重更新，但由于Tanh的取值输出以0对称，使用效果会比Sigmoid好很多。

torch.nn.ReLU（）对应的ReLU函数又叫修正线性单元，计算公式为：

 ReLU函数只保留大于0的输出，其他输出会设置为0.在输入正数的时候，不存在梯度饱和的问题。计算速度相对于其他类型的激活函数要快得多，而且ReLU函数只有线性关系，所以不管是前向传播还是反向传播，计算速度都很快。

torch.nn.Softplus()对应的平滑近似ReLU的激活函数，其计算公式为：

 

 默认取值为1.该函数对任意位置都可以计算导数，而且尽可能保留了ReLU激活函数的优点。

下面对以上四种激活函数进行可视化

import torch
from PIL import Image
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
x=torch.linspace(-6,6,100)

sigmoid=nn.Sigmoid()#Sigmoid函数
ysigmoid=sigmoid(x)

tanh=nn.Tanh()#Tanh激活函数
ytanh=tanh(x)

relu=nn.ReLU()
yrelu=relu(x)

softplus=nn.Softplus()#Softplus激活函数
ysoftplus=softplus(x)

plt.figure(figsize=(14,3))

plt.subplot(1,4,1)
plt.plot(x.data.numpy(),ysigmoid.data.numpy(),"r-")
plt.title("sigmoid")
plt.grid()

plt.subplot(1,4,2)
plt.plot(x.data.numpy(),ytanh.data.numpy(),"r-")
plt.title("tanh")
plt.grid()

plt.subplot(1,4,3)
plt.plot(x.data.numpy(),yrelu.data.numpy(),"r-")
plt.title("ReLU")
plt.grid()

plt.subplot(1,4,4)
plt.plot(x.data.numpy(),ysoftplus.data.numpy(),"r-")
plt.title("Softplus")
plt.grid()

plt.show()

 2.4 循环层

在pytorch中，提供了三种循环层的实现，分别如下表所示：

层对应的类	功能
torch.nn.RNN()	多层RNN单元
torch.nn.LSTM()	多层长短期记忆LSTM单元
torch.nn.GRU()	多层门循环GRU单元
torch.nn.RNNCell()	一个RNN循环层单元
torch.nn.LSTMCell()	一个长短期记忆LSTM单元
torch.nn.GRUCell()	一个门限环GRU单元

以torch.nn.RNN()输入一个多层的Elman RNN进行学习，激活函数可以使用tanh或者ReLU。对于输入序列中的每一个元素，RNN每层的计算公式为： 

 是时刻t的隐状态。是上一层时刻t的隐状态，或者是第一层在时刻t的输入。若nonlinearity=relu,则使用ReLU函数代替tanh函数作为激活函数。

下面以torch.nn.RNN()为例，介绍循环层的参数，输入和输出。

参数说明如下：

input_size:输入x的特征数量

hidden_size:隐藏层的特征数量

num_layers:RNN网络的层数

nonlinearity:指定非线性函数使用tanh还是relu,默认是tanh

bias:如果是False,那么RNN层就不会使用偏置权重，默认是True

batch_first：如果是True,那么输入和输出的shape应该是[batch_size,time_step,feature]

dropout:如果值非零，那么除了最后一层外，其他RNN层的输出都会套上一个dropout层，默认为0.

bidirectional:如果是True,将会变成一个双向RNN,默认为False

RNN的输入为input和h_0,其中input是一个形状为（seq_len,batch,input_size）的张量。h_0则是一个形状为（num_layers * num_directions,batch,hidden_size）保存着初始隐状态的张量。如果不提供就默认为0.如果是双向RNN,num_directions等于2，否则等于1.

RNN的输出为output和h_n,其中：ouyput是一个形状为（seq_len,batch,hidden_size * num_directions）的张量。保存着RNN最后一层的输出特征。如果输入是被填充过的序列，那么输出也是被填充过的序列。h_n是一个形状为（num_layers * num_directions,batch,hidden_size）的张量，保存着最后一个时刻的隐状态。

 2.5 全连接层

全连接层是指一个由多个神经元所组成的层，其所有的输出和该层的所有输入都有连接，即每个输入都会影响所有神经元的输出。在pytorch中的nn.Linear()表示线性变换，全连接层可以看做是nn.Linear()表示线性变层再加上一个激活函数层所构成的结构。

nn.Linear()全连接操作及相关参数如下：

torch.nn.Linear(in_features,out_features,bias=True)

参数说明如下：

in_features:每个输入样本的特征数量

out_features:每个输出样本的特征数量

bias:若设置为False，则该层不会学习偏置。默认值为True

torch.nn.Linear()的输入为（N,in_features）的张量，输出为（N,out_eatures）的张量。

全连接层组成的网络是全连接神经网络，可用于数据的分类或者回归预测，卷积神经网络和循环神经网络的末端通常会由多个全连接层组成。