数模笔记13-BP神经网络

BP神经网络算法

1. 什么是人工神经网络

   • “人工神经网络是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。”
   • 人工神经网络(ANN)具有自学习、自组织、较好的容错性和优良的非线性逼近能力。
   • 在实际应用中，80%～90%的人工神经网络模型是采用误差反传算法或其变化形式的网络模型。

2. ANN能干什么？

   数学近似映射（函数逼近）

   • 拟合—>预测
   • 分类—聚类分析

3. 神经网络模型和网络结构

   • 神经元模型
   • 激活函数
   • 网络结构
   • 工作状态
   • 学习方式

4. 建立和应用神经网络的步骤

   1. 网络结构的确定

      包含网络的拓扑结构和每个神经元相应函数的选取；

   2. 权值和阈值的确定

      通过学习得到，为有指导的学习，也就是利用已知的一组正确的输入、输出数据，调整权和阈值使得网络输出与理想输出偏差尽量小；

   3. 工作阶段

      用带有确定权重和阈值的神经网络解决实际问题的过程，也叫模拟（simulate）。

• 神经元信息传递

  神经元的信息传递和处理是一种电化学活动．树突由于电化学作用接受外界的刺激；通过胞体内的活动体现为轴突电位，当轴突电位达到一定的值则形成神经脉冲或动作电位；再通过轴突末梢传递给其它的神经元．从控制论的观点来看；这一过程可以看作一个多输入单输出非线性系统的动态过程。

• 人工神经元的模型

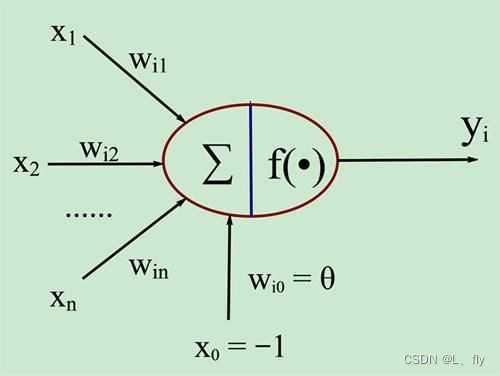
  • 作为神经网络的基本元素，神经元的模型如下：

    

    • x1~xn 是从其他神经元传来的输入信号
    • wij表示从神经元j到神经元i的连接权值
    • θ 表示一个阈值( threshold ) ，或称为偏置( bias )。

    $$\begin{gathered} 神经元的输出与输入的关系为： \\ 净激活量：ne{t}_i=\sum _{j=1}^n{w}_{ij}{x}_j-\theta =\sum _{j=0}^n{w}_{ij}{x}_j \\ 激活函数：y_i=f(ne{t}_i) \\ 若用X表示输入向量，用W表示权重向量： \\ X=[x_0,x_1,x_2,...,x_n],W=[w_{i0},w_{i1},w_{i2},...,w_{in}{]}^T \\ 则ne{t}_i=XW,y_i=f(XW) \end{gathered}$$

• 激活函数

  • 激活函数是对净激活量与输出进行映射的函数。一些常用的激活函数, 由于输入数据与期望值之间可能并不是量级一样，所以需要激活。

  • 线性函数
    $$f(x)=k\ast x+c$$

  • 阈值函数
    $$f(x)=\{\begin{array}{l}T,x>c\\ k\ast x,|x|\le c\\ -T,x<-c\end{array}$$

  • S形函数
    $$f(x)=\frac{1}{1+e^{-\alpha x}}$$

  • 双极S形函数
    $$f(x)=\frac{2}{1+e^{-\alpha x}}-1$$

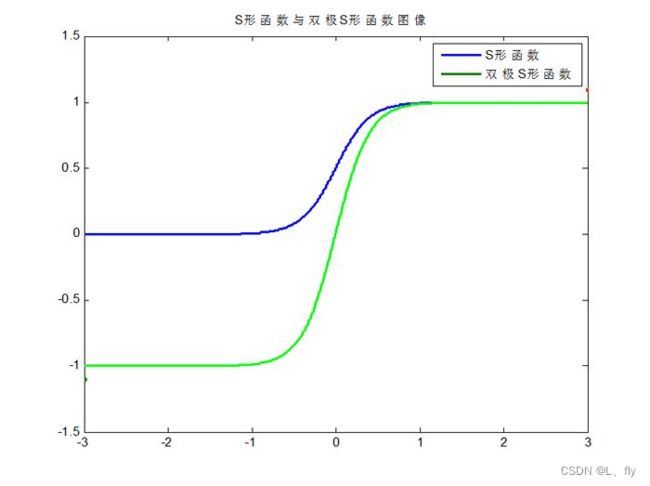
  S形函数和双极S形函数图像为：

  

  S形和双极S形函数的导函数均为连续函数。

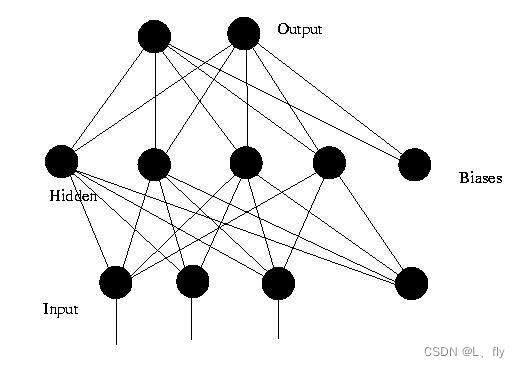
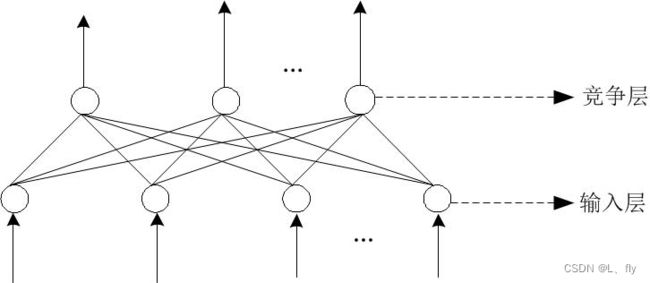
• 网络模型

  根据网络中神经元的互联方式的不同，网络模型分为：

  • 前馈神经网络

    只在训练过程会有反馈信号，而在分类过程中数据只能向前传送，直到到达输出层，层间没有向后的反馈信号

    

  • 反馈神经网络

    从输出到输入具有反馈连接的神经网络，其结构比前馈网络要复杂得多

    

  • 自组织网络

    通过自动寻找样本中的内在规律和本质属性，自组织、自适应地改变网络参数与结构。

    

• 工作状态

  神经网络的工作状态分为学习和工作两种状态

  • 学习

    利用学习算法来调整神经元间的连接权重，使得网络输出更符合实际

  • 工作

    神经元间的连接权值不变，可以作为分类器或者预测数据之用。

• 学习方式

  学习分为有导师学习与无导师学习

  • 有导师学习

    将一组训练集送入网络，根据网络的实际输出与期望输出间的差别来调整连接权

    例如：BP算法

  • 无导师学习

    抽取样本集合中蕴含的统计特性，并以神经元之间的联接权的形式存于网络中。

    例如：Hebb学习率

BP算法（Back Propagation）

采用BP学习算法的前馈神经网络称为BP神经网络

• BP算法基本原理

  利用输出后的误差来估计输出层的直接前导层的误差，再用这个误差估计更前一层的误差，如此一层一层的反传下去，就获得了所有其他各层的误差估计。

  信号的正向传播&误差的反向传播

  • 正向传播：

    – 输入样本－－－输入层－－－各隐层－－－输出层

  • 判断是否转入反向传播阶段：

    – 若输出层的实际输出与期望的输出不符

  • 误差反传

    – 误差以某种形式在各层表示－－－修正各层单元的权值

    网络输出的误差减少到可接受的程度进行到预先设定的学习次数为止

  ---

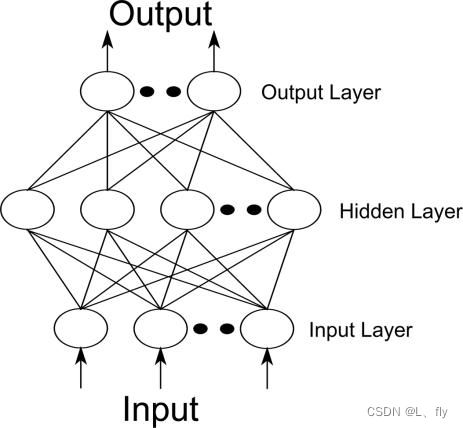
  假设输入层有n个神经元，隐含层有p个神经元 ，输出层有q个神经元

  • 符号定义

    • 输入向量；
      $$x=(x_1,x_2,...,x_n)$$

    • 隐含层输入向量；
      $$hi=(h{i}_1,h{i}_2,...,h{i}_p)$$

    • 隐含层输出向量；
      $$ho=(h{o}_1,h{o}_2,...,h{o}_p)$$

    • 输出层输入向量；
      $$yi=(y{i}_1,y{i}_2,...,y{i}_q)$$

    • 输出层输出向量；
      $$yo=(y{o}_1,y{o}_2,...,y{o}_q)$$

    • 期望输出向量；
      $$d_o=(d_1,d_2,...,d_q)$$

    • 误差函数
      $$e=\frac{1}{2}\sum _{o=1}^q(d_o(k)-y{o}_o(k){)}^2$$

  • 首先，计算各层神经元的输入和输出
    $$\begin{gathered} h{i}_h(k)=\sum _{i=0}^n{w}_{hi}{x}_i(k),h=1,2,...,p \\ h{o}_h(k)=f(h{i}_h(k)),h=1,2,...,p \\ y{i}_o(k)=\sum _{i=0}^p{w}_{oh}h{o}_h(k),o=1,2,...,q \\ y{o}_o(k)=f(y{i}_o(k)),o=1,2,...,q \end{gathered}$$

  • 第二步利用网络期望输出和实际输出，计算误差函数对输出层的各神经元的偏导数。
    $$\begin{gathered} \frac{\partial e}{\partial w_{oh}}=\frac{\partial e}{\partial y{i}_o}\frac{\partial y{i}_o}{\partial w_{oh}} \\ \frac{\partial e}{\partial y{i}_o}=\frac{\partial (\frac{1}{2}{\sum }_{o=1}^q(d_o(k)-y{o}_o(k){)}^2)}{\partial y{i}_o}=-(d_o(k)-y{o}_o(k))y{o}_o^{\prime }(k)=-(d_o(k)-y{o}_o(k))f^{\prime }(y{i}_o(k))\triangleq -{\delta }_o(k) \\ \frac{\partial y{i}_o(k)}{\partial w_{oh}}=\frac{\partial ({\sum }_h^p{w}_{oh}h{o}_h(k))}{\partial w_{oh}}=h{o}_h(k) \end{gathered}$$

  • 第三步：利用隐含层到输出层的连接权值、输出层的δ _ o(k)和隐含层的输出计算误差函数对隐含层各神经元的偏导数δ_h(k)。
    $$\begin{gathered} \frac{\partial e}{\partial w_{oh}}=\frac{\partial e}{\partial y{i}_o}\frac{\partial y{i}_o}{\partial w_{oh}}=-{\delta }_o(k)h{o}_h(k) \\ \frac{\partial e}{\partial w_{hi}}=\frac{\partial e}{\partial h{i}_h(k)}\frac{\partial h{i}_h(k)}{\partial w_{hi}} \\ \frac{\partial h{i}_h(k)}{\partial w_{hi}}=\frac{\partial ({\sum }_{i=0}^n{w}_{hi}{x}_i(k))}{\partial w_{hi}}=x_i(k) \\ \frac{\partial e}{\partial h{i}_h(k)}=\frac{\partial (\frac{1}{2}{\sum }_{o=1}^q(d_o(k)-y{o}_o(k){)}^2)}{\partial h{o}_h(k)}\frac{\partial h{o}_h(k)}{\partial h{i}_h(k)}=\frac{\partial (\frac{1}{2}{\sum }_{o=1}^q(d_o(k)-f(y{i}_o(k)){)}^2)}{\partial h{o}_h(k)}\frac{\partial h{o}_h(k)}{\partial h{i}_h(k)} \\ =\frac{\partial (\frac{1}{2}{\sum }_{o=1}^q((d_o(k)-f({\sum }_{o=1}^q{w}_{ho}h{o}_h(k){)}^2))}{\partial h{o}_h(k)}\frac{\partial h{o}_h(k)}{\partial h{i}_h(k)}=-\sum _{o=1}^q(d_o(k)-y{o}_o(k))f^{\prime }(y{i}_o(k))w_{ho}\frac{\partial h{o}_h(k)}{\partial h{i}_h(k)} \\ =-(\sum _{o=1}^q{\delta }_o(k)w_{ho})f^{\prime }(h{i}_h(k))\triangleq -{\delta }_h(k) \end{gathered}$$

  • 第四步，利用输出层各神经元的δ _ o(k)和隐含层各神经元的输出来修正连接权值w_oh(k)。
    $$\begin{gathered} △w_{oh}(k)=-\mu \frac{\partial e}{\partial w_{oh}}=\mu {\delta }_o(k)h{o}_h(k) \\ {w}_{oh}^{N+1}=w_{oh}^N+\mu {\delta }_o(k)h{o}_h(k) \\ \mu 是设置的学习率 \end{gathered}$$

  • 第五步，利用隐含层各神经元的δ _ h(k)和输入层各神经元的输入修正连接权。
    $$\begin{gathered} △w_{hi}(k)=-\mu \frac{\partial e}{\partial w_{hi}}={\delta }_h(k)x_i(k) \\ {w}_{hi}^{N+1}=w_{hi}^N+\mu {\delta }_h(k)x_i(k) \end{gathered}$$

  • 第六步，计算全局误差
    $$E=\frac{1}{2m}\sum _{k=1}^m\sum _{o=1}^q(d_o(k)-y_o(k){)}^2$$

  • 第七步，判断网络误差是否满足要求。当误差达到预设精度或学习次数大于设定的最大次数，则结束算法。否则，选取下一个学习样本及对应的期望输出，返回进入下一轮学习。