python计算机视觉第三章 图像到图像的映射

3.1单线性变换

单应性变换是将一个平面内的点映射到另一个平面内的二维投影变换。在这里，平
面是指图像或者三维中的平面表面。单应性变换具有很强的实用性，比如图像配准、
图像纠正和纹理扭曲，以及创建全景图像。

其实本质上就是一个单线性矩阵H，按照方程来映射图像二维

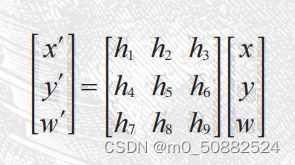
对于图像平面内（甚至是三维中）的点，齐次坐标是个非常有用的表示方式。点的齐次坐标是依赖于其尺度定义的，所以，x=[x,y,w]=[αx,αy,αw]=[x/w,y/w,1]都表示同一个二维点。因此，单应性矩阵H也仅依赖尺度定义，所以，单应性矩阵具有8个独立的自由度。我们通常使用w=1来归一化点，这样，点具有唯一的图像坐标x和y。这个额外的坐标是的我们可以简单地使用一个矩阵来表示变换。

def normallize(points):
    """在齐次坐标意义下，对点集进行归一化，是最后一行为1"""
    for row in points:
        row /= points[-1]
    return points
 
def make_homog(points):
    """将点集（dim×n的数组）转换为齐次坐标表示"""
 
    return vstack((points,ones((1, points.shape[1]))))
 

上面的程序可以实现对点的归一化处理以及转化齐次坐标的功能。

进行点和变换的处理时。我们会按照列优先的原则存储这些点。因此，n个二维点集将会存储为齐次坐标意义下的一个3×n数组。这种格式使得矩阵乘法和点的变换操作更加容易。对于其他的例子，比如对于聚类和分类的特征，我们将使用典型的行数组来存储数据。

在这些投影变换中，有一些特别重要的变换。比如，仿射变换

保持了 w=1, 不具有投影变换所具有的强大变形能力。仿射变换包含一个可逆矩阵 A
和一个平移向量 t=[tx,ty]。仿射变换可以用于很多应用，比如图像扭曲。

还有相似变换

是一个包含尺度变化的二维刚体变换。上式中的向量 s 指定了变换的尺度，R 是角
度为 θ 的旋转矩阵，t=[tx,ty] 在这里也是一个平移向量。

接下来设计用于估计单应性矩阵的算法，然后看一下使用仿射变
换进行图像扭曲，使用相似变换进行图像匹配，以及使用完全投影变换进行创建全
景图像的一些例子。

3.1.1直接线性变换算法

单应性矩阵可以有两幅图像（或者平面）中对应点对计算出来。前面已经提到过，一个完全射影变换具有8个自由度。根据对应点约束，每个对应点对可以写出两个方程，分别对应于x和y坐标。因此，计算单应性矩阵H需要4个对应点对。

DLT（Direct Linear Transformation，直接线性变换）是给定4个点或者更多对应点对矩阵，来计算单应性矩阵H的算法。将单应性矩阵H作用在对应点上，重新写出该方程，我们可以得到下面的方程：

或者Ah=0，其中A是一个具有对应点对二倍数量行数的矩阵。将这些对应点对方程的系数堆叠到一个矩阵红，我们可以使用SVD算法找到H的最小二乘解。下面是算法代码，我们也将其加入到 homography.py 文件里：

def H_from_points(fp, tp):
    """使用线性DLT方法，计算单应性矩阵H，使fp映射到tp。点自动进行归一化"""

    if fp.shape != tp.shape:
        raise RuntimeError('number of points do not match')

    # 对点进行归一化（对数值计算很重要）
    # --- 映射起始点 ---
    m = mean(fp[:2], axis=1)
    maxstd = max(std(fp[:2], axis=1)) + 1e-9
    C1 = diag([1 / maxstd, 1 / maxstd, 1])
    C1[0][2] = -m[0] / maxstd
    C1[1][2] = -m[1] / maxstd
    fp = dot(C1, fp)

    # --- 映射对应点 ---
    m = mean(tp[:2], axis=1)
    maxstd = max(std(tp[:2], axis=1)) + 1e-9
    C2 = diag([1 / maxstd, 1 / maxstd, 1])
    C2[0][2] = -m[0] / maxstd
    C2[1][2] = -m[1] / maxstd
    tp = dot(C2, tp)

    # 创建用于线性方法的矩阵，对于每个对应对，在矩阵中会出现两行数值
    nbr_correspondences = fp.shape[1]
    A = zeros((2 * nbr_correspondences, 9))
    for i in range(nbr_correspondences):
        A[2 * i] = [-fp[0][i], -fp[1][i], -1, 0, 0, 0,
                    tp[0][i] * fp[0][i], tp[0][i] * fp[1][i], tp[0][i]]
        A[2 * i + 1] = [0, 0, 0, -fp[0][i], -fp[1][i], -1,
                        tp[1][i] * fp[0][i], tp[1][i] * fp[1][i], tp[1][i]]

    U, S, V = linalg.svd(A)
    H = V[8].reshape((3, 3))

    # 反归一化
    H = dot(linalg.inv(C2), dot(H, C1))

    # 归一化，然后返回
    return H / H[2, 2]

上面的函数的第一步操作是检查点对两个数组中点的数目是否相同。如果不相同，函数将会抛出异常信息。这对于写出稳健的代码来说非常有用。

代码先对这些点进行归一化操作，使其均值为0，方差为1。因为算法的稳定性取决于坐标的表示情况和部分数值计算的问题，所以归一化操作非常重要。接下来我们使用对应点对来构造矩阵A。最小二乘解即为矩阵SVD分解后所得矩阵V的最后一行。该行经过变换后得到矩阵H。然后对这个矩阵进行处理和归一化，返回输出。

3.1.2仿射变换

由于仿射变换具有6个自由度，因此我们需要三个对应点来估计矩阵H。通过将最后两个元素设置为0，即h7=h8=0，仿射变换可以用上面的DLT算法估计得出。

下面的函数使用对应点来计算放射变换矩阵，我们继续将其添加到 homography.py 文件中。

def Haffine_from_points(fp, tp):
    """计算H仿射变换，使得tp是fp经过仿射变换H得到的"""

    if fp.shape != tp.shape:
        raise RuntimeError('number of points do not match')

    # 对点进行归一化（对数值计算很重要）
    # --- 映射起始点 ---
    m = mean(fp[:2], axis=1)
    maxstd = max(std(fp[:2], axis=1)) + 1e-9
    C1 = diag([1 / maxstd, 1 / maxstd, 1])
    C1[0][2] = -m[0] / maxstd
    C1[1][2] = -m[1] / maxstd
    fp_cond = dot(C1, fp)

    # --- 映射对应点 ---
    m = mean(tp[:2], axis=1)
    C2 = C1.copy()  # 两个点集，必须都进行相同的缩放
    C2[0][2] = -m[0] / maxstd
    C2[1][2] = -m[1] / maxstd
    tp_cond = dot(C2, tp)

    # 因为归一化后点的均值为0，所以平移量为0
    A = concatenate((fp_cond[:2], tp_cond[:2]), axis=0)
    U, S, V = linalg.svd(A.T)

    # 如Hartley和Zisserman著的Multiplr View Geometry In Computer,Scond Edition所示，
    # 创建矩阵B和C
    tmp = V[:2].T
    B = tmp[:2]
    C = tmp[2:4]

    tmp2 = concatenate((dot(C, linalg.pinv(B)), zeros((2, 1))), axis=1)
    H = vstack((tmp2, [0, 0, 1]))

    # 反归一化
    H = dot(linalg.inv(C2), dot(H, C1))

    return H / H[2, 2]

同样的，类似于DLT算法，这些点需要经过预处理和去处理化操作。

3.2图像扭曲

对图像块应用仿射变换，我们将其称为图像扭曲（或者 仿射扭曲）。该操作不仅经常在计算机图形学中，而且经常出现在计算机视觉算法总。扭曲的操作可以使用SciPy工具包中的ndimage包来简单完成。命令：

transform_im = ndimage.affine_transform(im, A, b, size)

使用上面所示的一个线性变换A和一个平移向量b来对图像块应用放射变换。选项参数 size 可以用来指定输出图像的大小。
下面我们可以运行来看一下是如何工作的

from numpy import *
from matplotlib.pyplot import *
from scipy import ndimage
from PIL import Image

# 解决中文乱码
rcParams['font.sans-serif'] = 'SimHei'
rcParams['axes.unicode_minus'] = False

im = array(Image.open('image/image1.jpg').convert('L'))
H = array([[1.4,0.05,-100],[0.05,1.5,-100],[0,0,1]])
im2 = ndimage.affine_transform(im, H[:2,:2],(H[0,2],H[1,2]))

gray()
subplot(121)
imshow(im)
title("原始图像")
axis('off')
subplot(122)
imshow(im2)
title("扭曲后的图像")
axis('off')
show()

分析：从实验结果我们可以看出来，原始图像（左）和扭曲后的图像（右）的差别，扭曲后的图像中丢失的像素用零来填充。

3.2.1图像中的图像

仿射扭曲的一个简单例子是，将图像或者图像的一部分放置在另一幅图像中，是的他们能够和指定的区域或者标记物对齐。

将函数 image_in_image() 添加到 wary.py 文件中。该函数的输入参数为两幅图像和一个坐标。该坐标为将第一幅图像放置到第二幅图像中的角点坐标：

3.2.2图像配准

图像配准是对图像进行变换，使变换后的图像能够在常见的坐标系中对齐。配准可
以是严格配准，也可以是非严格配准。为了能够进行图像对比和更精细的图像分析，
图像配准是一步非常重要的操作。

配准算法的一般步骤：

1 特征提取
特征提取是指分别提取两幅图像中共有的图像特征，这种特征是出现在两幅图像中对比列、旋转、平移等变换保持一致性的特征，如线交叉点、物体边缘角点、虚圆闭区域的中心等可提取的特征。特征包括：点、线和面三类。
2 特征匹配
对特征作描述
利用相似度准则进行特征匹配
3 估计变换模型
空间变换模型是所有配准技术中需要考虑的一个重要因素，各种配准技术都要建立自己的变换模型，变换空间的选取与图像的变形特性有关。常用的空间变换模型有：刚体变换、仿射变换、投影变换、非线性变换。
4 图像重采样及变换
在得到两幅图像的变换参数后，要将输入图像做相应参数的变换，使之与参考图像处于同一坐标系下，则矫正后的输入图像与参考图像可用作后续的图像融合、目标变化检测处理或图像镶嵌；涉及输入图像变换后所得点坐标不一定为整像素数，则应进行插值处理。常用的插值算法有最近领域法，双线性插值法和立方卷积插值法。
SIFT特征匹配算法包括两个阶段：

1 SIFT特征的生成
2 SIFT特征向量的匹配
SIFT特征向量的生成算法包括四步：

1 尺度空间极值检测，以初步确定关键点位置和所在尺度。
2 拟和三维二次函数精确确定位置和尺度，同时去除低对比度的关键点和不稳定的边缘响应点。
3 利用关键点领域像素的梯度方向分布特性为每个关键点指定参数方向，使算子具备旋转不变性。
4 生成SIFT特征向量

import numpy as np
import cv2
 
def sift_kp(image):
    gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    sift = cv2.xfeatures2d_SIFT.create()
    kp, des = sift.detectAndCompute(image, None)
    kp_image = cv2.drawKeypoints(gray_image, kp, None)
    return kp_image, kp, des
 
def get_good_match(des1, des2):
    bf = cv2.BFMatcher()
    matches = bf.knnMatch(des1, des2, k=2)
    good = []
    for m, n in matches:
        if m.distance < 0.75 * n.distance:
            good.append(m)
    return good
 
def siftImageAlignment(img1, img2):
    _, kp1, des1 = sift_kp(img1)
    _, kp2, des2 = sift_kp(img2)
    goodMatch = get_good_match(des1, des2)
    if len(goodMatch) > 4:
        ptsA = np.float32([kp1[m.queryIdx].pt for m in goodMatch]).reshape(-1, 1, 2)
        ptsB = np.float32([kp2[m.trainIdx].pt for m in goodMatch]).reshape(-1, 1, 2)
        ransacReprojThreshold = 4
        H, status = cv2.findHomography(ptsA, ptsB, cv2.RANSAC, ransacReprojThreshold);
        # 其中H为求得的单应性矩阵矩阵
        # status则返回一个列表来表征匹配成功的特征点。
        # ptsA,ptsB为关键点
        # cv2.RANSAC, ransacReprojThreshold这两个参数与RANSAC有关
        imgOut = cv2.warpPerspective(img2, H, (img1.shape[1], img1.shape[0]),
                                     flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP)
    return imgOut, H, status
 
img1 = cv2.imread('')
img2 = cv2.imread('')
while img1.shape[0] > 1000 or img1.shape[1] > 1000:
    img1 = cv2.resize(img1, None, fx=0.5, fy=0.5, interpolation=cv2.INTER_AREA)
while img2.shape[0] > 1000 or img2.shape[1] > 1000:
    img2 = cv2.resize(img2, None, fx=0.5, fy=0.5, interpolation=cv2.INTER_AREA)
 
result, _, _ = siftImageAlignment(img1, img2)
allImg = np.concatenate((img1, img2, result), axis=1)
cv2.namedWindow('1', cv2.WINDOW_NORMAL)
cv2.namedWindow('2', cv2.WINDOW_NORMAL)
cv2.namedWindow('Result', cv2.WINDOW_NORMAL)
cv2.imshow('1', img1)
cv2.imshow('2', img2)
cv2.imshow('Result', result)
# cv2.imshow('Result',allImg)
if cv2.waitKey(200000) & 0xff == ord('q'):
    cv2.destroyAllWindows()
    cv2.waitKey(1)

基于SIFT算法的图像配准，实验结果并没有跑出来，具体原因目前还有没找到。

3.3创建全景图

在同一位置（即图像的照相机位置相同）拍摄的两幅或者多幅图像是单应性相关的 。我们经常使用该约束将很多图像缝补起来，拼成一个大的图像来创建全景图像。在本节中，我们将探讨如何创建全景图像。

3.3.1RANSAC

RANSAC 是“RANdom SAmple Consensus”（随机一致性采样）的缩写。该方法是
用来找到正确模型来拟合带有噪声数据的迭代方法。给定一个模型，例如点集之间
的单应性矩阵，RANSAC 基本的思想是，数据中包含正确的点和噪声点，合理的模
型应该能够在描述正确数据点的同时摒弃噪声点。

RANSAC的基本假设是：

1 数据由“局内点”组成，例如：数据的分布可以用一些模型参数来解释；
2 “局外点”是不能适应该模型的数据；
3 除此之外的数据属于噪声。
局外点产生的原因有：噪声的极值；错误的测量方法；对数据的错误假设。

RANSAC也做了以下假设：给定一组（通常很小的）局内点，存在一个可以估计模型参数的过程；而该模型能够解释或者适用于局内点。

RANSAC算法的输入是一组观测数据，一个可以解释或者适应于观测数据的参数化模型，一些可信的参数。 RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点，并用下述方法进行验证：

1 首先我们先随机假设一小组局内点为初始值。然后用此局内点拟合一个模型，此模型适应于假设的局内点，所有的未知参数都能从假设的局内点计算得出。
2 用1中得到的模型去测试所有的其它数据，如果某个点适用于估计的模型，认为它也是局内点，将局内点扩充。
3 如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理。
4 然后，用所有假设的局内点去重新估计模型，因为此模型仅仅是在初始的假设的局内点估计的，后续有扩充后，需要更新。
5 最后，通过估计局内点与模型的错误率来评估模型。
整个这个过程为迭代一次，此过程被重复执行固定的次数，每次产生的模型有两个结 局：

要么因为局内点太少，还不如上一次的模型，而被舍弃。
要么因为比现有的模型更好而被选用。

iterations = 0
best_model = null
best_consensus_set = null
best_error = 无穷大
while ( iterations < k )
maybe_inliers = 从数据集中随机选择n个点
maybe_model = 适合于maybe_inliers的模型参数
consensus_set = maybe_inliers
 
for ( 每个数据集中不属于maybe_inliers的点 ）
if ( 如果点适合于maybe_model，且错误小于t ）
将点添加到consensus_set
if （ consensus_set中的元素数目大于d ）
已经找到了好的模型，现在测试该模型到底有多好
better_model = 适合于consensus_set中所有点的模型参数
this_error = better_model究竟如何适合这些点的度量
if ( this_error < best_error )
我们发现了比以前好的模型，保存该模型直到更好的模型出现
best_model =  better_model
best_consensus_set = consensus_set
best_error =  this_error
增加迭代次数
返回 best_model, best_consensus_set, best_error

RANSAC的优缺点
RANSAC的优点是它能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。RANSAC的缺点是它计算参数的迭代次数没有上限；如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型，概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。 RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型，RANSAC不能找到别的模型。

3.3.2稳健的单应性矩阵估计

我们在任何模型中都可以使用 RANSAC 模块。在使用 RANSAC 模块时，我们只需
要在相应 Python 类中实现 fit() 和 get_error() 方法，剩下就是正确地使用 ransac.py。
我们这里使用可能的对应点集来自动找到用于全景图像的单应性矩阵。

使用 SIFT 特征自动找到匹配对应：
可以通过运行一下的命令

import sift
featname = ['Univ'+str(i+1)+'.sift' for i in range(5)]
imname = ['Univ'+str(i+1)+'.jpg' for i in range(5)]
l = {}
d = {}
for i in range(5):
 sift.process_image(imname[i],featname[i])
 l[i],d[i] = sift.read_features_from_file(featname[i]) 
matches = {}
for i in range(4):
 matches[i] = sift.match(d[i+1],d[i])

但是，并不是所有图像中的对应点对都是正确的。实际上，SIFT 是具有很强稳健性
的描述子，能够比其他描述子，例如图像块相关的 Harris 角点，产生更少的错误的
匹配。但是该方法仍然远非完美。

3.3.3拼接图像

估计出图像间的单应性矩阵（使用 RANSAC 算法），现在我们需要将所有的图像扭
曲到一个公共的图像平面上。通常，这里的公共平面为中心图像平面（否则，需要
进行大量变形）。一种方法是创建一个很大的图像，比如图像中全部填充 0，使其和
中心图像平行，然后将所有的图像扭曲到上面。由于我们所有的图像是由照相机水平
旋转拍摄的，因此我们可以使用一个较简单的步骤：将中心图像左边或者右边的区域填充０，以便为扭曲的图像腾出空间。

# -*- coding: utf-8 -*-
from pylab import *
from numpy import *
from PIL import Image
 
# If you have PCV installed, these imports should work
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift
 
"""
This is the panorama example from section 3.3.
"""
 
# 设置数据文件夹的路径
featname = ['G:\\picture\\path\\' + str(i + 1) + '.sift' for i in range(5)]
imname = ['G:\\picture\\path\\' + str(i + 1) + '.jpg' for i in range(5)]
 
# 提取特征并匹配使用sift算法
l = {}
d = {}
for i in range(5):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])
 
matches = {}
for i in range(4):
    matches[i] = sift.match(d[i + 1], d[i])
 
# 可视化匹配
for i in range(4):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i + 1]))
    figure()
    sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)
 
 
# 将匹配转换成齐次坐标点的函数
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j + 1][ndx, :2].T)
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2, :2].T)
 
    # switch x and y - TODO this should move elsewhere
    fp = vstack([fp[1], fp[0], fp[2]])
    tp = vstack([tp[1], tp[0], tp[2]])
    return fp, tp
 
 
# 估计单应性矩阵
model = homography.RansacModel()
 
fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0]  # im 1 to 2
 
fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0]  # im 0 to 1
 
tp, fp = convert_points(2)  # NB: reverse order
H_32 = homography.H_from_ransac(fp, tp, model)[0]  # im 3 to 2
 
tp, fp = convert_points(3)  # NB: reverse order
H_43 = homography.H_from_ransac(fp, tp, model)[0]  # im 4 to 3
 
# 扭曲图像
delta = 2000  # for padding and translation用于填充和平移
 
im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12,im1,im2,delta,delta)
 
im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12,H_01),im1,im_12,delta,delta)
 
im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32,im1,im_02,delta,delta)
 
im1 = array(Image.open(imname[4]), "f")
im_42 = warp.panorama(dot(H_32,H_43),im1,im_32,delta,2*delta)
 
figure()
imshow(array(im_42, "uint8"))
axis('off')
show()
 

实验并没有跑出来，解决方法还在寻找中，但是从书本中的例子可以看出，创建的全景图结果正如你所看到的，图像曝光不同，在单个图像的边界上存在边缘效
应。商业的创建全景图像软件里有额外的操作来对强度进行归一化，并对平移进行
平滑场景转换，以使得结果看上去更好。

在这次的学习里我遇到了不少困难包括库的安装与实验代码的调试，同时也发现了很多自己的不足，本章内容仍旧需要继续加强学习。