线性代数之 矩阵求导(3)标量、向量求导的快速记忆
线性代数之 矩阵求导(3)标量、向量求导的快速记忆
- 前言
- 基本约定
- 引例
-
- 标量对标量求导
- 标量对向量求导
- 向量对向量求导
- 包含两个变量的求导
- 总结
- 扩展
前言
上一次记录了矩阵求导的基本法则和公式,并且大部分给出了基于矩阵乘法的证明(本质证明)。然而这样记忆矩阵求导还是比较困难的。
这里给出一种作者使用的快速记忆矩阵求导的方法。
注意:该方法仅是作者个人记忆用方法,公式推导并不严格符合数学规范。
基本约定
默认向量是列向量。只涉及标量对向量,向量对向量的求导。
本次矩阵求导默认使用分子布局,即分子不变分母转置。
引例
标量对标量求导
我们都知道下面函数的求导:
f ( x 0 ) = a x 0 2 + b x 0 + c f ′ ( x 0 ) = 2 a x 0 + b f(x_0)=ax_0^2+bx_0+c \\ f'(x_0)=2ax_0+b f(x0)=ax02+bx0+cf′(x0)=2ax0+b
其中,多项式的系数写在自变量的前面。我们把这种表示叫做变量后置。对于标量而言,变量前置后置是没有区别的。
标量对向量求导
先看一个分母布局的例子:
f ( x ) = a T x ∂ ( a T x ) T / ∂ x = a f(x)=a^Tx \\ \quad \\ \partial (a^Tx)^T/\partial x= a f(x)=aTx∂(aTx)T/∂x=a
a T x a^Tx aTx这个标量对列向量求导,得到列向量 a a a。但是结果出现了 a T a^T aT的转置,不好记。
而从直观的角度上, ∂ ( a T x ) / ∂ x = a T \partial (a^Tx)/\partial x= a^T ∂(aTx)/∂x=aT这种类似标量对标量求导的表示更符合我们的思维直觉。
分子布局刚好符合这种直觉:
f ( x ) = a T x ∂ ( a T x ) / ∂ x T = a T f(x)=a^Tx \\ \quad \\ \partial (a^Tx)/\partial x^T= a^T f(x)=aTx∂(aTx)/∂xT=aT
只是分子布局里出现了 ∂ x T \partial x^T ∂xT。不过没有关系,我们认为通过分子布局进行求导时默认 ∂ x \partial x ∂x是 ∂ x T \partial x^T ∂xT。那么就有:
f ( x ) = a T x ∂ ( a T x ) / ∂ x = a T f(x)=a^Tx \\ \quad \\ \partial (a^Tx)/\partial x= a^T f(x)=aTx∂(aTx)/∂x=aT
这么记起来就容易多了。我们管这样的表达方法叫后置变量求导,系数不变。
那么对应的就有前置变量求导,系数前置并转置:
f ( x ) = x T a ∂ ( x T a ) / ∂ x = ∂ ( x T a ) T / ∂ x = a T f(x)=x^Ta \\ \quad \\ \partial (x^Ta)/\partial x =\partial (x^Ta)^T/\partial x= a^T f(x)=xTa∂(xTa)/∂x=∂(xTa)T/∂x=aT
总而言之,后置变量求导,系数的位置和表示不变;前置变量求导,系数的位置要前置,表示要转置。
向量对向量求导
对于向量之间的求导,以上记忆方法仍然是成立的。举例:
∂ ( A x ) / ∂ x = A ∂ ( x T A ) / ∂ x = A T \partial (Ax)/\partial x =A \\ \partial (x^TA)/\partial x =A^T \\ ∂(Ax)/∂x=A∂(xTA)/∂x=AT
包含两个变量的求导
以下函数包含两个变量:
f ( x ) = x T A x f(x)=x^TAx \\ \quad \\ f(x)=xTAx
对于这种函数,可以类比标量对标量的乘积求导:
∂ ( x T A x ) / ∂ x = ∂ ( ( x T ) ( A x ) ) / ∂ x 对 于 前 置 变 量 x T , A x 是 系 数 , 系 数 要 前 置 并 转 置 对 于 后 置 复 合 变 量 A x , x T 是 系 数 , 系 数 不 变 ∂ ( ( x T ) ( A x ) ) / ∂ x = ( A x ) T ∂ ( x T ) / ∂ x + x T ∂ ( A x ) / ∂ x = x T A T + x T A \partial (x^TAx)/\partial x=\partial ((x^T)(Ax))/\partial x \\ \quad \\ 对于前置变量x^T,Ax是系数,系数要前置并转置\\对于后置复合变量Ax,x^T是系数,系数不变 \\ \quad \\ \partial ((x^T)(Ax))/\partial x = (Ax)^T\partial (x^T)/\partial x\\+x^T\partial (Ax)/\partial x\\ =x^TA^T+x^TA ∂(xTAx)/∂x=∂((xT)(Ax))/∂x对于前置变量xT,Ax是系数,系数要前置并转置对于后置复合变量Ax,xT是系数,系数不变∂((xT)(Ax))/∂x=(Ax)T∂(xT)/∂x+xT∂(Ax)/∂x=xTAT+xTA
总结
标量对向量求导,默认使用分子布局并默认用 ∂ x \partial x ∂x简写 ∂ x T \partial x^T ∂xT, a T x a^Tx aTx被称为变量 x x x后置, x T a x^Ta xTa称为变量 x x x前置,对后置变量求导系数不变,对前置变量求导系数转置并前置。
举例1:
∂ ( a T x x T b ) / ∂ x 把 乘 积 变 成 两 个 变 量 的 乘 积 形 式 ∂ ( a T x x T b ) / ∂ x = ∂ ( ( a T x ) ( x T b ) ) / ∂ x = x T b ∂ ( a T x ) / ∂ x + ( a T x ) ∂ ( x T b ) / ∂ x = x T b a T + a T x b T = x T b a T + x T a b T \partial (a^Txx^Tb)/\partial x \\ \quad \\ 把乘积变成两个变量的乘积形式 \\ \quad \\ \partial (a^Txx^Tb)/\partial x = \partial ((a^Tx)(x^Tb))/\partial x \\ = x^Tb\partial (a^Tx)/\partial x+(a^Tx)\partial (x^Tb)/\partial x \\ = x^Tba^T+a^Txb^T=x^Tba^T+x^Tab^T ∂(aTxxTb)/∂x把乘积变成两个变量的乘积形式∂(aTxxTb)/∂x=∂((aTx)(xTb))/∂x=xTb∂(aTx)/∂x+(aTx)∂(xTb)/∂x=xTbaT+aTxbT=xTbaT+xTabT
举例2:
∂ ( x T x ) / ∂ x 这 个 式 子 可 写 作 ∂ ( ∥ x ∥ 2 ) / ∂ x ∂ ( x T x ) / ∂ x = x T + x T = 2 x T \partial (x^Tx)/\partial x \\ \quad \\ 这个式子可写作\partial (\Vert x \Vert^2)/\partial x \\ \quad \\ \partial (x^Tx)/\partial x = x^T+x^T=2x^T ∂(xTx)/∂x这个式子可写作∂(∥x∥2)/∂x∂(xTx)/∂x=xT+xT=2xT
举例3:
∂ ( A x + b ) T C ( D x + e ) / ∂ x = ( C ( D x + e ) ) T ∂ ( A x + b ) T / ∂ x + ( A x + b ) T C ∂ ( D x + e ) / ∂ x = ( D x + e ) T C T A + ( A x + b ) T C D \partial (Ax+b)^TC(Dx+e)/\partial x\\ =(C(Dx+e))^T\partial (Ax+b)^T/\partial x + (Ax+b)^TC\partial (Dx+e)/\partial x \\ =(Dx+e)^TC^TA+(Ax+b)^TCD ∂(Ax+b)TC(Dx+e)/∂x=(C(Dx+e))T∂(Ax+b)T/∂x+(Ax+b)TC∂(Dx+e)/∂x=(Dx+e)TCTA+(Ax+b)TCD
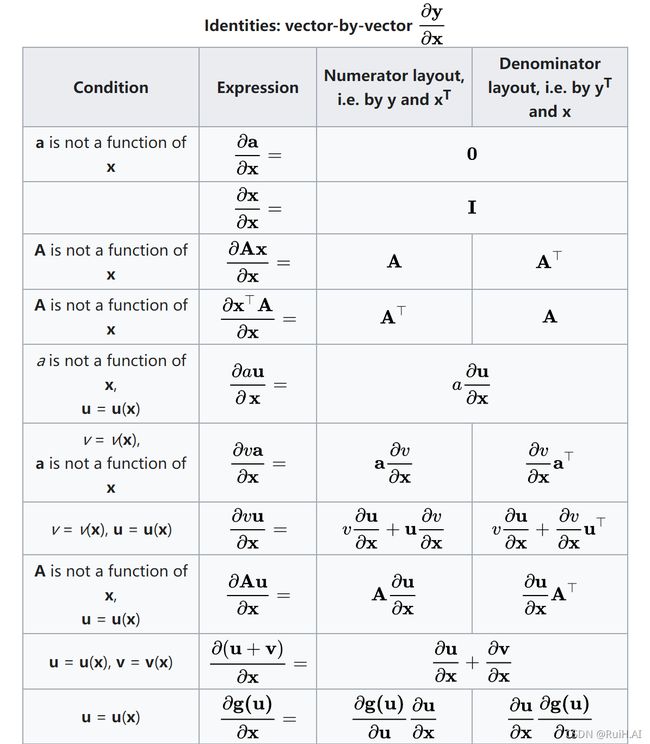
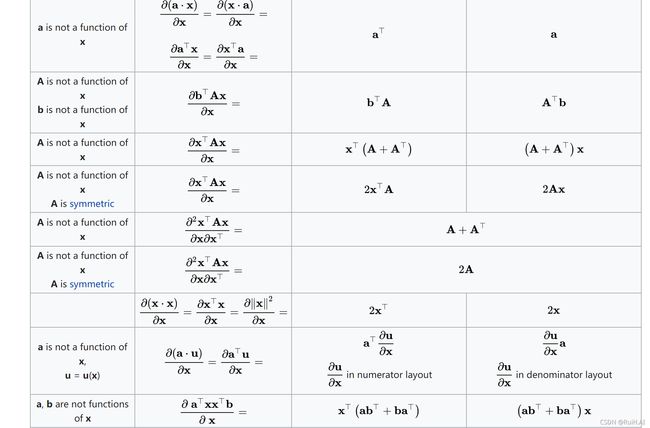
这里给出一个wiki上的求导法则和公式做对照:
向量对向量求导:
标量对向量:

扩展
对于分母布局而言,其快速记忆法其实刚好与以上相反:后置变量,系数后置并转置,前置变量,系数不变。其实就是分子布局求导结果的转置。