从Transformer到ViT:多模态编码器算法原理解析与实现
从Transformer到ViT:多模态编码器算法原理解析与实现
- 模型架构与算法原理
-
- Image Token Embedding
- Multi-head Self-attention流程
-
- 线性变换
- MatMul
- Scale和softmax
- MatMul
- 前向层模块
- ADD NORM模块
- 思考
- 多模态模型应用的感想
- Paddle实现vit模型
Transformer架构是一种使用自注意力机制的神经网络,最初是由谷歌提出的,被广泛应用于自然语言处理和图像处理任务中。它是一种基于注意力机制的深度学习模型,适用于序列到序列的学习任务,例如机器翻译、语音识别、文本摘要等。
多模态Transformer前部分encoder算法是近年来在计算机视觉领域备受瞩目的研究方向之一。它的出现极大地推动了多模态信息的融合与处理,被广泛应用于图像、文本等多种数据类型的处理。
其中,Vision Transformer(ViT)是一种以Transformer为基础的视觉编码器,已经在各种视觉任务中取得了极佳的效果。本篇博客将介绍多模态Transformer前部分encoder算法的原理,重点讲解其在ViT中的实现,同时附带完整的ViT代码实现。如果您对多模态Transformer前部分encoder算法感兴趣,或是对ViT的实现方式想要深入了解,本文或许能为您提供帮助。
下面是vit模型核心架构图,下文是对模型架构各部分做了详细的介绍。
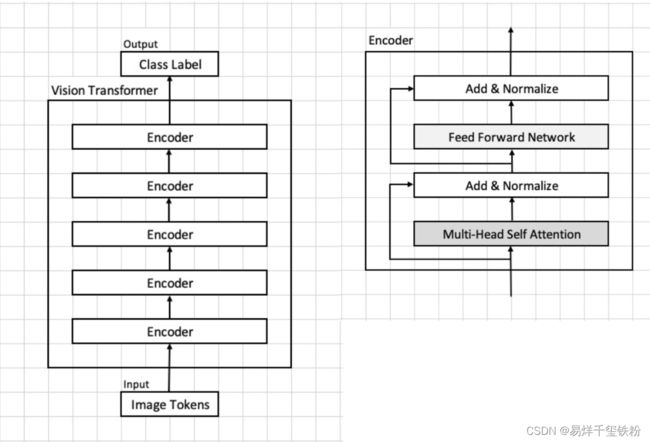
模型架构与算法原理
Image Token Embedding
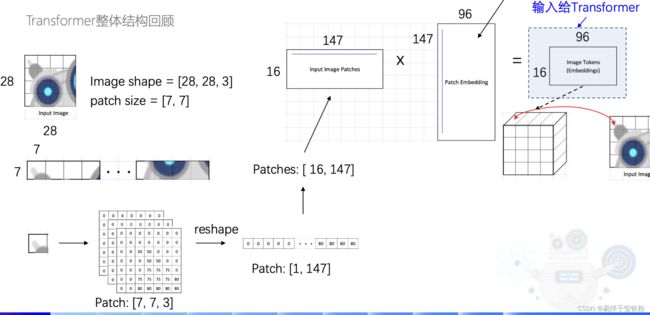
模型输入一个将一张28x28x3的图片,模型先将图片切成一个16块,每一块为7x7。还是3通道的。
再将7x7,3通道的数据,并成一行,[1,7x7x3]=[1,147],
有16块那就是[16,147]。
接着将图片转为特征向量Embedding:
I m a g e 16 ∗ 147 Image_{16*147} Image16∗147* W 147 ∗ 96 W_{147*96} W147∗96= E m b e d d i n g Embedding Embedding
其中 W 147 ∗ 96 W_{147*96} W147∗96就是要训练的参数,也就是下图中的Patch Embedding,
Multi-head Self-attention流程
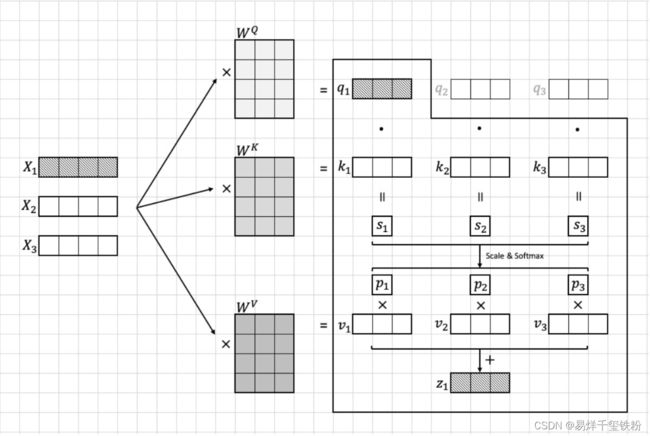
依据模型输入的图片转换为的Image token Embedding,我们假设这个图像块集合为 [ x 1 , x 2 , . . . , x 16 ] [{x_1, x_2, ..., x_{16}}] [x1,x2,...,x16],每个图像块的维度为 96 × 16 96 \times 16 96×16,接着将这个embedding输入到transformer中。

在transformer首先进入到Multi-head Self-attention进行以下四个步骤:线性变换、多头机制、scale和softmax、多头机制。下面我们将逐步说明这些步骤的算法流程。
线性变换
我们首先将每个图像块 x i x_i xi映射到一个10维的向量 z i z_i zi。
这个映射是通过对 x i x_i xi做一个线性变换得到的,具体而言,我们将 x i x_i xi乘以一个 96 × 10 96 \times 10 96×10的权重矩阵 W q W_q Wq得到一个10维的向量 z i z_i zi:
 z i = W q a i z_i = W_q a_i zi=Wqai
z i = W q a i z_i = W_q a_i zi=Wqai
其中 z i z_i zi向量包含有 q i , k i , v i q_i,k_i,v_i qi,ki,vi,模型训练需要算出参数有三个变换矩阵 W q , W k , W v W_q,W_k,W_v Wq,Wk,Wv
MatMul
我们计算每个图像块 x i x_i xi与其他所有图像块的注意力分数。具体而言,我们计算每对图像块 ( x i , x j ) (x_i, x_j) (xi,xj)的注意力分数 a i , j a_{i,j} ai,j,并将其用于加权求和所有图像块的向量表示。
为了计算注意力分数,我们需要先计算每对图像块之间的“相似度”
这个相似度是通过将 q i q_i qi与 k j k_j kj做点积得到的。
其中, q i q_i qi和 k j k_j kj分别是图像块 i i i和图像块 j j j通过线性变换得到的向量。这个点积的结果可以看作是两个向量的余弦相似度,用于衡量它们之间的相似程度, i ∈ [ 1 , 16 ] , j ∈ [ 1 , 16 ] i \in[1,16],j\in [1,16] i∈[1,16],j∈[1,16]
s j = q i ⋅ k j s_j = q_i \cdot k_j sj=qi⋅kj
Scale和softmax
然而,直接计算点积可能会因为向量维度较大而导致计算上的不稳定性,因此我们在计算前先将 q i q_i qi和 k j k_j kj除以一个缩放因子 10 \sqrt{10} 10,就是特征的维度10,从而保证点积的值较小,不容易出现计算上的不稳定性,然后在进行softmax函数计算。
具体公式如下:
p j = s o f t m a x ( ∑ i ∑ j q i ⋅ k j 10 ) = q i ⋅ k j 10 ∑ i ∑ j q i ⋅ k j 10 p_j =softmax(\sum_{i}\sum_{j}\frac{q_i \cdot k_j}{\sqrt{10}})=\frac{ \frac{q_i \cdot k_j}{\sqrt{10}}}{\sum_{i}\sum_{j} \frac{q_i \cdot k_j}{\sqrt{10}}} pj=softmax(i∑j∑10qi⋅kj)=∑i∑j10qi⋅kj10qi⋅kj
其中, ⋅ \cdot ⋅ 表示向量点积运算。注意力分数的分母 10 \sqrt{10} 10是一个缩放因子,用于确保点积的结果不会过大或过小。
MatMul
最后结合向量 v i v_i vi计算出 x i x_i xi的注意力特征向量 z i z_i zi:
z i = ∑ i i = 16 p i ∗ v i z_i=\sum_{i}^{i=16} p_i*v_i zi=∑ii=16pi∗vi
具体流程可以看下图
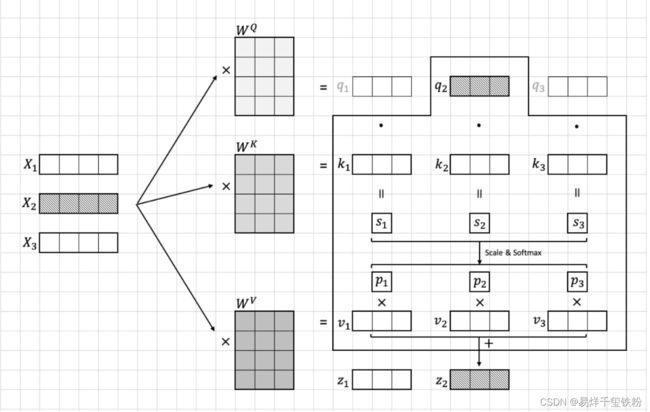
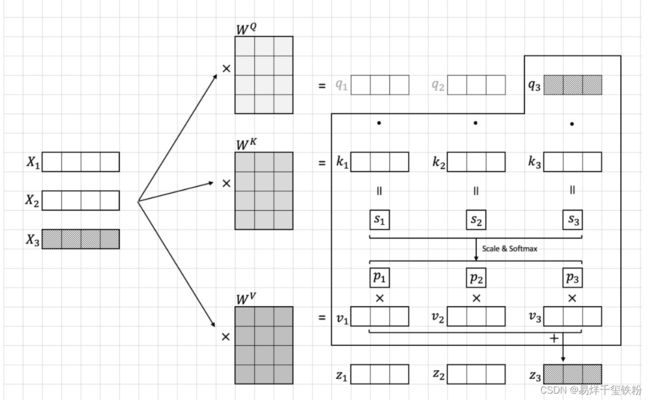
上面这种是对于自注意力的,还有一种多注意力
多注意力实现其实就是多个自注意力这样的结构结合起来,如下图所示

上面的 x x x,就是 [ x 1 , x 2 , x 3 , . . . , x 16 ] [x_1,x_2,x_3,...,x_{16}] [x1,x2,x3,...,x16]组合起来,以第一个自注意力来看, Q 1 , K 1 , V 1 Q_1,K_1,V_1 Q1,K1,V1其实就是自注意力里的 [ q 1 , q 2 , q 3 , . . . , q 16 ] , [ k 1 , k 2 , k 3 , . . . , k 16 ] , [ v 1 , v 2 , v 3 , . . . , v 16 ] [q_1,q_2,q_3,...,q_{16}],[k_1,k_2,k_3,...,k_{16}],[v_1,v_2,v_3,...,v_{16}] [q1,q2,q3,...,q16],[k1,k2,k3,...,k16],[v1,v2,v3,...,v16]
多头只是从计算上来说,每一个自注意的q不仅要与自己的k和v计算,还要结合其他的自注意的k和v计算。
最简单的例子来理解注意力,举例一个生活的例子来说
当我们将自注意力算法类比为一个学生学习一门学科的过程时,可以将 q q q看作是学生的注意力, k k k看作是这门学科的大纲, v v v则代表着这个学科的教材的内容。通过计算 q q q与 k k k的相似度,可以得到学生消耗注意力与大纲中不同知识点之间的分配权重,从而确定学生应该集中注意力去学习哪些知识点。最后,通过将这些权重乘以 v v v,可以得到学生学习到的知识内容。
多头注意力算法可以被类比为一个学生在学习多门学科的情况。在这种情况下,不同的学科可能具有不同的难度、内容和格式。因此,学生的注意力在不同的学科中可能有所不同。通过多头注意力算法,我们可以将学生的注意力 q q q与不同学科大纲中的知识点 k k k以及学科的教材内容 v v v相乘,从而得到不同学科下的学习成果。这样做的好处是,可以更好地利用不同学科中的优势,进一步提高学生的学习效果。
前向层模块
前向层模块由两个全连接层和一个残差连接组成。残差连接将输入直接添加到模块的输出上。全连接层包括一个线性变换和一个激活函数,其中线性变换将输入 x 乘以一个权重矩阵 W1,并加上偏置 b1,然后将结果输入激活函数进行非线性转换。激活函数通常为 ReLU。
前向层模块的计算公式如下:
F F N ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 + x \mathrm{FFN}(x) = \max(0, xW_1+b_1)W_2+b_2 + x FFN(x)=max(0,xW1+b1)W2+b2+x
其中 x x x 表示输入, W 1 W_1 W1 和 b 1 b_1 b1 是第一个全连接层的权重矩阵和偏置向量, W 2 W_2 W2 和 b 2 b_2 b2 是第二个全连接层的权重矩阵和偏置向量。
ADD NORM模块
ADD NORM 模块由一个残差连接和一个 Layer Normalization 组成。残差连接将输入直接添加到模块的输出上。Layer Normalization 用于归一化每个样本在不同维度上的特征。
ADD NORM 模块的计算公式如下:
L a y e r N o r m ( x + S u b l a y e r ( x ) ) \mathrm{LayerNorm}(x+\mathrm{Sublayer}(x)) LayerNorm(x+Sublayer(x))
其中 x x x 表示输入,Sublayer 表示 Transformer 模型中的一个子层(如自注意力模块或前向层模块)。 x + S u b l a y e r ( x ) x+\mathrm{Sublayer}(x) x+Sublayer(x) 表示输入加上子层的输出。LayerNorm 对 x + S u b l a y e r ( x ) x+\mathrm{Sublayer}(x) x+Sublayer(x) 进行归一化。
思考
搞懂了算法各结构的原理,如下是我个人的几个思考
为什么这种transformer结构,将原始特征向量通过与上下文(或者上下图像)的相似度计算,得出的新的特征向量能够更准确的代表这个数据的特征向量呢?
Transformer 结构在自然语言处理和计算机视觉等领域广泛应用,主要原因是它具有以下优点:
- 上下文信息丰富。相比于传统的基于手工设计特征的方法,Transformer能够利用上下文信息对特征向量进行更加准确的表示。在自然语言处理中,上下文可以是当前单词所处的句子或段落,而在计算机视觉中,上下文可以是当前像素所处的图像区域。
- 处理长序列能力强。由于使用了自注意力机制,Transformer 能够对长序列进行有效的处理。在自然语言处理中,这使得Transformer 能够处理长文本,而在计算机视觉中,这使得 Transformer 能够对高分辨率的图像进行处理。
- 端到端的学习。Transformer结构能够直接从原始数据中学习特征表示,而无需手工设计特征。这使得模型能够从原始数据中学习到更加准确的特征表示,从而提高了模型的性能。
为什么多头注意力,比自注意力效果更好呢
多头注意力是一种在 Transformer 模型中使用的注意力机制,相比于单独使用自注意力机制,它能够提高模型的表现。这主要是由于以下几个原因:
- 多头注意力能够并行处理不同信息。在多头注意力中,模型使用多个注意力头同时学习不同的信息。这意味着模型能够并行处理多个不同的信息,从而加速模型的训练和推断过程。
- 多头注意力能够学习更加复杂的特征表示。由于多头注意力能够并行处理多个信息,模型能够学习更加复杂的特征表示。这能够帮助模型捕捉更加丰富和多样化的特征,从而提高模型的表现。
- 多头注意力能够提高模型的泛化能力。在多头注意力中,每个注意力头都能够学习不同的特征表示,这使得模型更加鲁棒并能够更好地泛化到新的数据。
总的来说,多头注意力能够并行处理多个信息,学习更加复杂的特征表示,并提高模型的泛化能力,这使得它比单独使用自注意力机制效果更好。
在transformer中encoder叠加了多个,它的作用是什么呢,是不断更精细化的求出图像与图像相似度之间的关系吗
在 Transformer 模型中,encoder 叠加了多个层,每个层都包含了多头注意力和前馈神经网络。encoder 叠加多层的作用是逐渐提取和组合输入序列中的信息,并生成更加准确的特征表示。这些特征表示最终被用于后续的任务,如机器翻译、语言模型、文本分类等。
具体来说,encoder 中的每一层都能够进一步优化模型的特征表示。通过多层叠加,模型能够逐渐捕捉输入序列中的更多信息,从而生成更加准确的特征表示。这些特征表示能够反映输入序列中的重要信息,并能够被用于后续的任务。
因此,encoder 叠加多层的作用并不是仅仅更精细地求出图像与图像之间的相似度,而是逐渐提取和组合输入序列中的信息,生成更加准确的特征表示,从而提高模型的性能。在计算机视觉任务中,输入序列可能是图像的像素值序列或者是图像的特征表示序列,而不仅仅是图像与图像之间的相似度。
多模态模型应用的感想
掌握了transformer就是前半部分,就算是知道了,我们现在有的数据图像、语音、文本是如何转为模型的特征向量了,
能获取到这些特征向量,应该说就可以输出任何标签类的任务,从实现原理熵也就是在transformer结构下游,增加全连接层实现输出。(这也是在大模型中使用预训练模型微调的一种方法)。

Paddle实现vit模型
# ViT Online Class
# Author: Dr. Zhu
# Project: PaddleViT (https://github.com/BR-IDL/PaddleViT)
# 2021.11
import paddle
import paddle.nn as nn
import numpy as np
from PIL import Image
paddle.set_device('cpu')
class Identity(nn.Layer):
def __init__(self):
super().__init__()
def forward(self, x):
return x
class Mlp(nn.Layer):
def __init__(self, embed_dim, mlp_ratio=4.0, dropout=0.):
super().__init__()
self.fc1 = nn.Linear(embed_dim, int(embed_dim * mlp_ratio))
self.fc2 = nn.Linear(int(embed_dim * mlp_ratio), embed_dim)
self.act = nn.GELU()
self.dropout = nn.Dropout(dropout)
def forward(self, x):
x = self.fc1(x)
x = self.act(x)
x = self.dropout(x)
x = self.fc2(x)
return x
class PatchEmbedding(nn.Layer):
def __init__(self, image_size, patch_size, in_channels, embed_dim, dropout=0.):
super().__init__()
self.patch_embedding = nn.Conv2D(in_channels, embed_dim, patch_size, patch_size)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
# [n, c, h, w]
x = self.patch_embedding(x) # [n, c', h', w']
x = x.flatten(2) # [n, c', h'*w']
x = x.transpose([0, 2, 1]) # [n, h'*w', c']
x = self.dropout(x)
return x
class Attention(nn.Layer):
# TODO: 补全时,删除pass
def __init__(self, embed_dim, num_heads, qkv_bias=False, qk_scale=None, dropout=0., attention_dropout=0.):
super().__init__()
self.num_heads = num_heads
self.attn_head_size = int(embed_dim / self.num_heads)
self.all_head_size = self.attn_head_size * self.num_heads
self.qkv = nn.Linear(embed_dim, self.all_head_size*3)
if qk_scale == None:
self.scales = self.attn_head_size ** -0.5
else:
self.scales = qk_scale
self.proj = nn.Linear(self.all_head_size, embed_dim)
self.attn_dropout = nn.Dropout(attention_dropout)
self.proj_dropout = nn.Dropout(dropout)
self.softmax = nn.Softmax(axis=-1)
def transpose_multihead(self, x):
new_shape = x.shape[:-1] + [self.num_heads, self.attn_head_size]
x = x.reshape(new_shape)
x = x.transpose([0, 2, 1, 3])
return x
def forward(self, x):
qkv = self.qkv(x).chunk(3, axis=-1)
q, k, v = map(self.transpose_multihead, qkv)
attn = paddle.matmul(q, k, transpose_y=True)
attn = attn * self.scales
attn = self.softmax(attn)
attn_weights = attn
attn = self.attn_dropout(attn)
z = paddle.matmul(attn, v)
z = z.transpose([0, 2, 1, 3])
new_shape = z.shape[:-2] + [self.all_head_size]
z = z.reshape(new_shape)
z = self.proj(z)
z = self.proj_dropout(z)
return z, attn_weights
class EncoderLayer(nn.Layer):
def __init__(self, embed_dim):
super().__init__()
self.attn_norm = nn.LayerNorm(embed_dim)
self.attn = Attention()
self.mlp_norm = nn.LayerNorm(embed_dim)
self.mlp = Mlp(embed_dim)
def forward(self, x):
h = x
x = self.attn_norm(x)
x = self.attn(x)
x = x + h
h = x
x = self.mlp_norm(x)
x = self.mlp(x)
x = x + h
return x
class ViT(nn.Layer):
def __init__(self):
super().__init__()
self.patch_embed = PatchEmbedding(224, 7, 3, 16)
layer_list = [EncoderLayer(16) for i in range(5)]
self.encoders = nn.LayerList(layer_list)
self.head = nn.Linear(16, 10)
self.avgpool = nn.AdaptiveAvgPool1D(1)
self.norm = nn.LayerNorm(16)
def forward(self, x):
x = self.patch_embed(x) # [n, h*w, c]: 4, 1024, 16
for encoder in self.encoders:
x = encoder(x)
# avg
x = self.norm(x)
x = x.transpose([0, 2, 1])
x = self.avgpool(x)
x = x.flatten(1)
x = self.head(x)
return x
def main():
t = paddle.randn([4, 16, 96])
print('input shape = ', t.shape)
model = Attention(embed_dim=96, num_heads=8,
qkv_bias=False, qk_scale=None, dropout=0., attention_dropout=0.)
print(model)
out, attn_weights = model(t)
print(out.shape)
print(attn_weights.shape)
if __name__ == "__main__":
main()