html5 Canvas画图6:曲线之arcTo
上一篇文章讲了canvas的arc方法,这一篇讲和他有关的arcTo方法。
arc与arcTo,从名字都能看出来相似。arcTo也是画曲线的方法,而且他画出的曲线也是正圆的一段弧线。但他的参数和arc简直是不共戴天~
ctx.arcTo(x1,y1,x2,y2,radius);
arcTo的参数中包括两个点,而且这两个点中并没有表示圆心的点,仅仅最后的参数是圆的半径,表示arcTo和圆有那么点关系。
网上关于arcTo的文章很少,好不容易找到一篇还是外国的;而且canvas画图木有直观工具,只能靠猜,arcTo害我猜了半天。。
为了直观的描述,我采取了一种辅助办法:arcTo画到哪里,我就用lineTo也画到相应的点,以查看他们的关系。就是画辅助线。
var x0=100, y0=400, x1 = 500, y1 = 400, x2 = 450, y2 = 450; ctx.beginPath(); ctx.moveTo(x0,y0); ctx.strokeStyle = "#f00"; ctx.lineWidth = 2; ctx.arcTo(x1,y1,x2,y2,20); ctx.stroke(); ctx.beginPath(); ctx.strokeStyle = "rgba(0,0,0,0.5)"; ctx.lineWidth = 1; ctx.moveTo(x0,y0); ctx.lineTo(x1,y1); ctx.fillText('x1,y1',x1+10,y1+10) ctx.lineTo(x2,y2); ctx.fillText('x2,y2',x2+10,y2) ctx.stroke();
看起来代码有点多,其实很简单。我用了几个变量来保存坐标值,其余的都是canvas的操作了。
变量说明:x0,y0是起点坐标,x1,y1是第一个点坐标,x2,y2就是第二个点坐标。其中lineTo画的直线是半透明的1px黑线,arcTo画的线条是2px的红线。
刷新页面,即可看到下图。

不得不说这条红线很像一个钩子。
于是arcTo的规律就找到了,他其实是通过起点,第1点,第2点的两条直线,组成了一个夹角,而这两条线,也是参数圆的切线。
其中圆的半径决定了圆会在什么位置与线条发生切边。就像一个球往一个死角里面滚,球越小就滚得越进去,越靠近死角;球大则反之。
这是一个很严肃的学术问题,大家可不要YY。
让我们把球球变大吧!
ctx.arcTo(x1,y1,x2,y2,50); //半径改成50

如图,你可以看到圆弧变得很大,甚至都不和直线相切了。
当然,实际上他们还是相切的,因为切线是无限延长的。
我们继续探索,把圆继续变大,把起点与第1点的距离缩短。
var x0=400; //起点x坐标从100变400 ... ctx.arcTo(x1,y1,x2,y2,100); //圆的半径变大到100
然后你就会看到这么个奇特的图形。
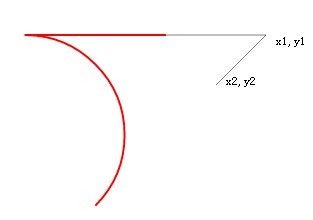
本来是个钩子,现在被硬生生的掰弯了,还掰到反方向了!有点像酒瓶架了。
不过,大家注意看,这个圆依然是和两条线相切的!只是现在两条线的长度都满足不了这个圆了!他已经把两条线都无线延长了!
这个钩子柄什么时候会发生反转呢?如果你几何学的好,你可以试着理解一下点与圆的切线方程。。
arcTo方法中有个很重要的点,这个重要的点就是代码中的(x1,y1),只要他到圆的切点的距离,超过了他到起点(x0,y0)的距离,就会发生反转。
从图中我们可以看到,(x2,y2)这个点的坐标可以无限变化,只要他始终是切线上的一个点,那么在圆的半径不变的情况下,arcTo画出的图形不会有任何变化。这点需要特别注意。
让我用我拿不上台面的几何知识来验证下这个命题吧。为了方便计算,我先把两条线的夹角改成90度。
var x0=100, y0=400, x1 = 500, y1 = 400, x2 = 500, y2 = 450;
更改后就是90度张开了哟!我们保持球的半径不变。刷新后:
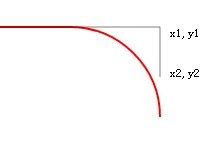
我们把y2变大,也就是延长了一条切线,把他变成550,刷新后:
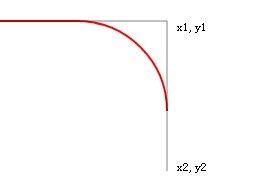
切线是延长了,但arcTo画出的红线没有任何变化。