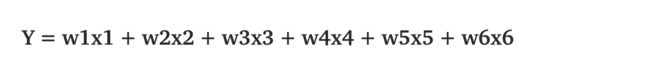遗传算法实例解析(python)
一.简介
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传机理的生物学进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
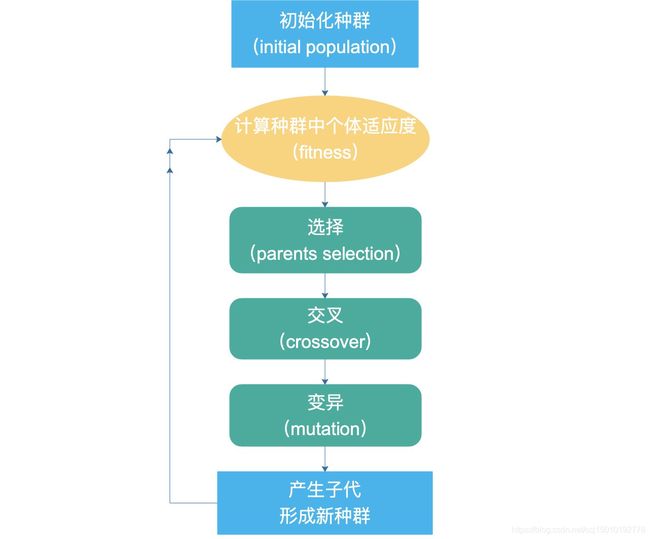
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。
二.遗传算法图解过程
三.程序实例
(一)题目简介
最大化目标函数Y。
其中(x1,x2,x3,x4,x5,x6)=(4,-2,3.5,5,-11,-4.7),求w1,w2,w3,w4,w5,w6。
(二)分步程序
1. 初始种群:
随机生成8个solution,即生成8组w1,w2,w3,w4,w5,w6。
# Inputs of the equation.
equation_inputs = [4,-2,3.5,5,-11,-4.7]
# Number of the weights we are looking to optimize.
num_weights = len(equation_inputs) # 6
sol_per_pop = 8
num_parents_mating = 4
# Defining the population size:shape(8,6).
pop_size = (sol_per_pop,num_weights)
# The population will have sol_per_pop chromosome where each chromosome has num_weights genes.
# Creating the initial population.
new_population = numpy.random.uniform(low=-4.0, high=4.0, size=pop_size)
print("initial population:")
print(new_population) # 输出随机生成的(8,6)population矩阵2.计算适应度:
计算每个solution的fitness,即带入公式计算出Y的值。
# 计算fitness
def cal_pop_fitness(equation_inputs, pop):
# Calculating the fitness value of each solution in the current population.
# The fitness function calculates the sum of products between each input and its corresponding weight.
fitness = numpy.sum(pop * equation_inputs, axis=1) # 每一行6位对应相乘相加得出和,一共计算出8个和值
return fitness
a = cal_pop_fitness(equation_inputs,new_population)
print('\ninitial fitness:\n', a)
# 输出计算出的8个solution的fitness值: (8,6)*(6,1)=(8,1)3.选择:
根据fitness值从大到小,选择最大的4个作为parent,以便后续交叉、变异生成子代。
# 选择parents
def select_mating_pool(pop, fitness, num_parents):
# Selecting the best individuals in the current generation as parents for producing the offspring of the next generation.
parents = numpy.empty((num_parents, pop.shape[1])) # parents用来存放被选择的parent,shape:(4,6)
for parent_num in range(num_parents):
max_fitness_idx = numpy.where(fitness == numpy.max(fitness))
# print(max_fitness_idx) 存的是array([3],),所以需要下一步取出具体的值3
max_fitness_idx = max_fitness_idx[0][0]
# print(max_fitness_idx)
parents[parent_num, :] = pop[max_fitness_idx, :] # 将fitness值大的solution放入parent
fitness[max_fitness_idx] = -99999999999 # 将已选的solution的fitness值赋为很小,以免再被选到
return parents
b = select_mating_pool(new_population,a,num_parents_mating)
print('\nparents:\n',b)
4.交叉:
随机生成一个数作为交叉点开始位置,从交叉点起始后的片段进行交叉。parent1与parent2交叉,把交叉第一个结果作为子代offspring1,同样,parent2与parent3交叉得到offspring2,parent3与parent4交叉得到offspring3,parent4与parent1交叉得到offspring4.
# 单点交叉crossover
def crossover(parents, offspring_size):
offspring = numpy.empty(offspring_size)
# The point at which crossover takes place between two parents. Usually, it is at the center.
crossover_point = numpy.uint8(offspring_size[1] / 2) # 6/2=3
print('\ncrossover point: ',crossover_point)
for k in range(offspring_size[0]):
# Index of the first parent to mate.
parent1_idx = k % parents.shape[0]
# Index of the second parent to mate.
parent2_idx = (k + 1) % parents.shape[0]
# The new offspring will have its first half of its genes taken from the first parent.
offspring[k, 0:crossover_point] = parents[parent1_idx, 0:crossover_point]
# The new offspring will have its second half of its genes taken from the second parent.
offspring[k, crossover_point:] = parents[parent2_idx, crossover_point:]
return offspring
offspring_size = (pop_size[0]-b.shape[0],num_weights) # 8-4=4
c = crossover(b,offspring_size)
print('crossover offspring:\n',c)
5.变异:
随机生成一个数,作为变异数。假定变异位为4,将交叉后生成的offspring每个位置4上的值都加上变异数,形成新的4个子代。
# 随机变异mutation
def mutation(offspring_crossover):
# Mutation changes a single gene in each offspring randomly.
for idx in range(offspring_crossover.shape[0]):
# The random value to be added to the gene.
random_value = numpy.random.uniform(-1.0, 1.0, 1)
# print(random_value) 随机生成突变数
offspring_crossover[idx, 4] = offspring_crossover[idx, 4] + random_value
return offspring_crossover
d = mutation(c)
print('\nmutation offspring:\n',d)
6.新种群:
将4个新生成的offspring加入原有的parents,形成新的种群。
# 新种群:4 parents+4 offsprings
new_population[0:b.shape[0], :] = b
new_population[b.shape[0]:, :] = d
print("\nnew population:\n",new_population)
7.计算新种群fitness
# 计算新种群fitness
e = cal_pop_fitness(equation_inputs,new_population)
print("\nnew population fitness:\n",e)
一次迭代过程结束。
(三)完整一次迭代程序
一次迭代程序完整代码如下:
import numpy
'''
一次迭代遗传算法实例
-----------------------------------------
The y=target is to maximize this equation:
y = w1x1+w2x2+w3x3+w4x4+w5x5+6wx6
where (x1,x2,x3,x4,x5,x6)=(4,-2,3.5,5,-11,-4.7)
What are the best values for the 6 weights w1 to w6?
------------------------------------------
原种群:随机生成8个solution
计算fitness:计算8个solution的fitness值
选择parent:fitness较高的其中4个solution
生成offspring:parent交叉、变异生成4个新的solution
新种群:4个parent + 4个offspring
计算新种群的fitness,观察是否有改进
------------------------------------------
'''
# Inputs of the equation.
equation_inputs = [4,-2,3.5,5,-11,-4.7]
# Number of the weights we are looking to optimize.
num_weights = len(equation_inputs) # 6
sol_per_pop = 8
num_parents_mating = 4
# Defining the population size:shape(8,6).
pop_size = (sol_per_pop,num_weights)
# The population will have sol_per_pop chromosome where each chromosome has num_weights genes.
# Creating the initial population.
new_population = numpy.random.uniform(low=-4.0, high=4.0, size=pop_size)
print("initial population:")
print(new_population) # 输出随机生成的(8,6)population矩阵
# 计算fitness
def cal_pop_fitness(equation_inputs, pop):
# Calculating the fitness value of each solution in the current population.
# The fitness function calculates the sum of products between each input and its corresponding weight.
fitness = numpy.sum(pop * equation_inputs, axis=1) # 每一行6位对应相乘相加得出和,一共计算出8个和值
return fitness
a = cal_pop_fitness(equation_inputs,new_population)
print('\ninitial fitness:\n', a)
# 输出计算出的8个solution的fitness值: (8,6)*(6,1)=(8,1)
# 选择parents
def select_mating_pool(pop, fitness, num_parents):
# Selecting the best individuals in the current generation as parents for producing the offspring of the next generation.
parents = numpy.empty((num_parents, pop.shape[1])) # parents用来存放被选择的parent,shape:(4,6)
for parent_num in range(num_parents):
max_fitness_idx = numpy.where(fitness == numpy.max(fitness))
# print(max_fitness_idx) 存的是array([3],),所以需要下一步取出具体的值3
max_fitness_idx = max_fitness_idx[0][0]
# print(max_fitness_idx)
parents[parent_num, :] = pop[max_fitness_idx, :] # 将fitness值大的solution放入parent
fitness[max_fitness_idx] = -99999999999 # 将已选的solution的fitness值赋为很小,以免再被选到
return parents
b = select_mating_pool(new_population,a,num_parents_mating)
print('\nparents:\n',b)
# 单点交叉crossover
def crossover(parents, offspring_size):
offspring = numpy.empty(offspring_size)
# The point at which crossover takes place between two parents. Usually, it is at the center.
crossover_point = numpy.uint8(offspring_size[1] / 2) # 6/2=3
print('\ncrossover point: ',crossover_point)
for k in range(offspring_size[0]):
# Index of the first parent to mate.
parent1_idx = k % parents.shape[0]
# Index of the second parent to mate.
parent2_idx = (k + 1) % parents.shape[0]
# The new offspring will have its first half of its genes taken from the first parent.
offspring[k, 0:crossover_point] = parents[parent1_idx, 0:crossover_point]
# The new offspring will have its second half of its genes taken from the second parent.
offspring[k, crossover_point:] = parents[parent2_idx, crossover_point:]
return offspring
offspring_size = (pop_size[0]-b.shape[0],num_weights) # 8-4=4
c = crossover(b,offspring_size)
print('crossover offspring:\n',c)
# 随机变异mutation
def mutation(offspring_crossover):
# Mutation changes a single gene in each offspring randomly.
for idx in range(offspring_crossover.shape[0]):
# The random value to be added to the gene.
random_value = numpy.random.uniform(-1.0, 1.0, 1)
# print(random_value) 随机生成突变数
offspring_crossover[idx, 4] = offspring_crossover[idx, 4] + random_value
return offspring_crossover
d = mutation(c)
print('\nmutation offspring:\n',d)
# 新种群:4 parents+4 offsprings
new_population[0:b.shape[0], :] = b
new_population[b.shape[0]:, :] = d
print("\nnew population:\n",new_population)
# 计算新种群fitness
e = cal_pop_fitness(equation_inputs,new_population)
print("\nnew population fitness:\n",e)
(四)程序输出结果
initial population:
[[ 1.49671815 0.93113301 1.52468311 2.1008358 0.52596433 1.98108016]
[ 0.02967332 3.04681893 1.97656438 2.7959895 3.15241166 3.91648211]
[-1.31178987 -1.27418233 -1.00478326 -1.29114282 1.8485721 3.13817543]
[ 2.65273704 1.00240443 3.92621841 1.7364455 1.46130962 -3.52271109]
[ 1.51475644 -2.1725475 1.47089756 -3.69968089 2.24351239 2.65613884]
[-2.54748948 1.26403815 -0.09425664 3.68666271 -1.41268268 -3.59376827]
[ 0.58807659 -0.57318307 -2.12536315 -1.06865911 3.62827415 -0.47741893]
[ 0.72622601 1.08531417 -1.14659535 -0.95386063 -1.96272369 -0.51242958]]
initial fitness:
[ 4.86849204 -38.16101585 -47.75496796 31.51246754 -40.10863106
37.81560145 -46.95054081 15.95026854]
parents:
[[-2.54748948 1.26403815 -0.09425664 3.68666271 -1.41268268 -3.59376827]
[ 2.65273704 1.00240443 3.92621841 1.7364455 1.46130962 -3.52271109]
[ 0.72622601 1.08531417 -1.14659535 -0.95386063 -1.96272369 -0.51242958]
[ 1.49671815 0.93113301 1.52468311 2.1008358 0.52596433 1.98108016]]
crossover point: 3
crossover offspring:
[[-2.54748948 1.26403815 -0.09425664 1.7364455 1.46130962 -3.52271109]
[ 2.65273704 1.00240443 3.92621841 -0.95386063 -1.96272369 -0.51242958]
[ 0.72622601 1.08531417 -1.14659535 2.1008358 0.52596433 1.98108016]
[ 1.49671815 0.93113301 1.52468311 3.68666271 -1.41268268 -3.59376827]]
mutation offspring:
[[-2.54748948 1.26403815 -0.09425664 1.7364455 2.1462265 -3.52271109]
[ 2.65273704 1.00240443 3.92621841 -0.95386063 -2.7350463 -0.51242958]
[ 0.72622601 1.08531417 -1.14659535 2.1008358 0.21911624 1.98108016]
[ 1.49671815 0.93113301 1.52468311 3.68666271 -2.21451672 -3.59376827]]
new population:
[[-2.54748948 1.26403815 -0.09425664 3.68666271 -1.41268268 -3.59376827]
[ 2.65273704 1.00240443 3.92621841 1.7364455 1.46130962 -3.52271109]
[ 0.72622601 1.08531417 -1.14659535 -0.95386063 -1.96272369 -0.51242958]
[ 1.49671815 0.93113301 1.52468311 2.1008358 0.52596433 1.98108016]
[-2.54748948 1.26403815 -0.09425664 1.7364455 2.1462265 -3.52271109]
[ 2.65273704 1.00240443 3.92621841 -0.95386063 -2.7350463 -0.51242958]
[ 0.72622601 1.08531417 -1.14659535 2.1008358 0.21911624 1.98108016]
[ 1.49671815 0.93113301 1.52468311 3.68666271 -2.21451672 -3.59376827]]
new population fitness:
[ 37.81560145 31.51246754 15.95026854 4.86849204 -11.41745433
50.07252895 -4.4959844 69.14470585]对比new population fitness 和 initial fitness,结果有了很大改善。初始解中最大值是37.81560145,经过遗传算法一次选择交叉变异后,最大值变为了69.14470585,效果显著。循环多次选择交叉变异过程,将越来越接近最优解。
参考资料:
https://www.jianshu.com/p/ae5157c26af9
https://towardsdatascience.com/genetic-algorithm-implementation-in-python-5ab67bb124a6