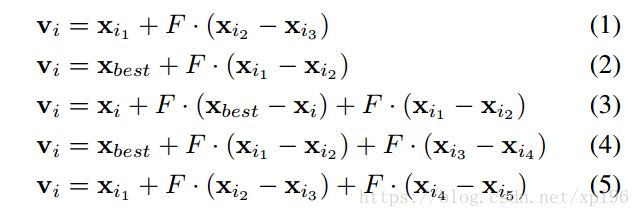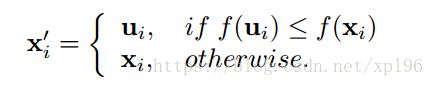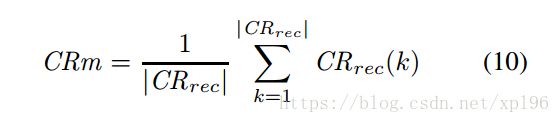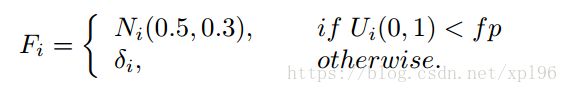优化算法 —— SaNSDE

一、背景介绍

传统的差分进化 (DE) 包括几种变异策略以及三个控制参数：种群大小 NP，缩放因子 F，以及交叉率 CR，除了 NP 是对所有基于种群的算法是通用的之外，变异策略，参数 F，CR 对问题的适应度是 DE 搜索过程中最关键的问题。

Self-adaptive Differential Evolution with Neighborhood Search (SaNSDE) 是对 NSDE 进行了一些改进，参考了 SaDE 中提出的一些方法。SaDE 中主要侧重于交叉率 CR 的适应度以及对不同变异策略的自适应（变异策略通常是很依赖问题的），NSDE 没有采用自适应的策略，通过参数 F 将不同的 NS 算子（NS 策略的细节可以参考演化编程）的搜索偏差混合起来；SaNSDE 继承了 SaDE 中的自适应变异方案，并且采用自适应策略调整 NSDE 中的参数 fp，通过加权策略对 SaDE 中 CR 的自适应能力做了一下改进。

二、算法介绍

2.1 标准 DE 算法

基本的 DE 算法中，个体表示为一组 D 维向量，演化过程包括了变异、交叉、选择三个部分：

1. 差分进化变异的基本公式为序号 (1) (2)，i1，i2，i3 均选择的与 i 不相同的个体，其中公式 (2) 的基准个体为 best，具有更强的收敛性； 缩放因子 F 在标准 DE 中通常设置为常量  F = 0.5；

2. 差分进化交叉操作是针对维度进行的，新个体有 CR 的概率选择 vi 中的维度，其余维度选择 xi，j = j rand 保证了 ui 中一定有某一维度是来自于 vi 中，否则会额外浪费一次进化机会。CR 在标准 DE 中通常设置为 CR = 0.9；

3. 选择操作在于在变异个体 ui 和旧个体 xi 中选取更好的个体，生成的新个体 xi’ 是 xi 的子代（本文以最小化问题举例）。

2.2 NSDE 算法

NSDE 是 DE 算法的一个变种，利用了演化编程 (EP) 中邻域搜索 (NS) 的策略，NSDE 基本与标准 DE 类似，区别在于对缩放因子 F 做了进一步的调整：

i 是当前目标个体的索引，Ui(0, 1) 表示 0 - 1 之间均匀分布的向量，Ni (0.5, 0.5) 表示均值，标准差均为 0.5 的高斯分布，delta i 表示尺度参数 t = 1 的柯西随机变量， 参数 fp 在NSDE 中设置为常量 fp = 0.5；

NSDE 相较于标准 DE 的优势在于，在没有先验知识的情况下，NSDE 可以不陷入局部最优解。

2.3 SaDE 算法

SaDE 尝试使用两种不同的变异策略， 用以解决变异策略高度依赖于问题的难题。算法引入了概率 p 来控制选择变异策略，p 根据学习经验进行自适应，此外， p 引入了两种方式用以自适应 DE 中的参数 F 和 CR，如下所示：

1. 变异策略自适应：p 初始化为 p = 0.5，当种群在本轮全部演化完成后，记录分别由公式 (1) 和公式 (3) 成功进入下一代的个体数 ns1，ns2，以及由公式 (1) 和公式 (3) 没有进入下一代的个体数 nf1，nf2；对这两组数分别记录 50 代，称为“学习周期”，概率 p 由公式 (8) 计算，当概率 p 在学习周期之后更新完毕，重设 ns1，ns2，nf1，nf2的值。

2. 参数 F 的设置：

3. 自适应交叉率 CR (SaCR)：SaDE 中给每一个个体都分配了交叉率 CRi，CRm 初始化为 CRm = 0.5，种群中 CRi 每 5 代进行一次更新。每一代中，CRm 的值与子代成功进入下一代相关，进入下一代的个体对应的 CRi 进入数组 CRrec 中，每隔 25 代进行一次更新，更新完后，对 CRrec 数组进行一次清空。

2.4 SaNSDE

SaNSDE 算法主要在于吸取 SaDE 和 NSDE 算法的优势，一方面使得所有参数自适应，另一方面希望引入邻域搜索不至于陷入局部最优解，综上提出的算法如下：

1. 变异策略：采用与 SaDE 相同的变异策略，即公式 (7) (8). 

2. 自适应缩放因子 F：SaNSDE 继承了 NSDE 中对 F 的参数设置，并将 fp 动态化，采用公式 (8) 中的 p 值作为新的 fp 值

3. 自适应加权交叉率 CR (SaCRW)：SaNSDE 采用了 SaDE 中自适应 CR 的策略，并对此作了部分改进，对 CRm 进行了加权处理，在记录 CRrec 的同时，计算当前适应值变化 delta frec，并将该值引入 CRm 中：

参数 CR 决定了变异向量有多少成分能进入下一代的候选解当中，所以，从同一个父代获得的子代中，较小的 CR 值更有可能优于父代个体。综上，SaCR 中的 CRm 在自适应过程中会隐性偏向于较小的 CR 值。当处理不可分函数时，这种偏向会降低优化性能，因为需要更大 CR 值来同时改变不可分的变量；

在进一步实验之后，可以假设较大的 CR 值会对不可分函数有更大的改进，因为可以对不可分变量同时进行改变，所以可以通过基于提升适应值大小对 SaCR 进行加权，用以平衡 SaCR 中的偏向，实验结果证明了该方案的有效性。

---

[1] Yang Z, Tang K, Yao X. Self-adaptive differential evolution with neighborhood search[C]//Evolutionary Computation, 2008. CEC 2008.(IEEE World Congress on Computational Intelligence). IEEE Congress on. IEEE, 2008: 1110-1116.