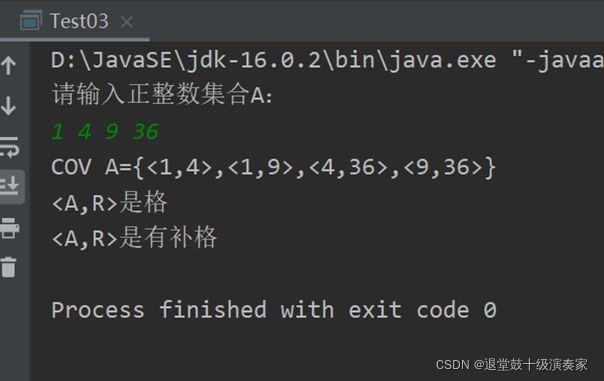
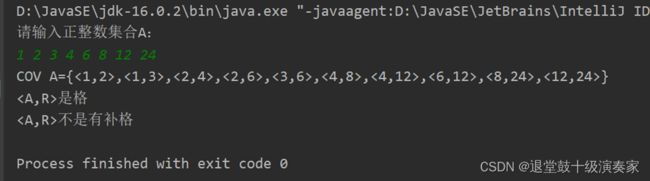
士兵过河2025B卷目录点击查看:华为OD机试2025B卷真题题库目录|机考题库+算法考点详解华为OD2025B卷200分题型题目描述一支N个士兵的军队正在趁夜色逃亡,途中遇到一条湍急的大河。敌军在T的时长后到达河面,没到过对岸的士兵都会被消灭。现在军队只找到了1只小船,这船最多能同时坐上2个士兵。当1个士兵划船过河,用时为a[i];0<=i
Spring MVC 架构详解
Java廖志伟
Java场景面试宝典SpringMVCWebApplicationDevelopmentMVCArchitecture
我是廖志伟,一名Java开发工程师、《Java项目实战——深入理解大型互联网企业通用技术》(基础篇)、(进阶篇)、(架构篇)清华大学出版社签约作家、Java领域优质创作者、CSDN博客专家、阿里云专家博主、51CTO专家博主、产品软文专业写手、技术文章评审老师、技术类问卷调查设计师、幕后大佬社区创始人、开源项目贡献者。拥有多年一线研发和团队管理经验,研究过主流框架的底层源码(Spring、Spri
仓颉编程语言:从入门到精通
为啥要瞅瞅仓颉这玩意儿?有一说一,现在的编程语言多得跟米一样,对吧?那一门新语言想火,没点绝活儿肯定不行。仓颉(Cangjie)这哥们儿,是华为搞出来的新玩意儿,静态编译的,主打的就是一个现代化、性能炸裂、安全感满满,而且天生就会搞并发。就凭这几点,已经有不少大佬开始关注了。这篇博客呢,就是你的“老司机”指南,带你把仓颉这车开得明明白白。不管你是刚上路的小白,还是开惯了Rust、Go、Java、N
java组件化设计_构建之路—谈谈组件化后端构建和实现
前言这一篇文章,准备了很久,构思了很久,草稿了很久。从个人编程至今,历经了C,C++,Java,到现如今的NodeJS。也后端到前端,再回到后端。更从学校里的学生信息管理系统到大型商业系统构建,是的,我曾一直以为编程也就是如此了,由瀑布模型,敏捷开发,设计模式等等组成的软件工程大致就是如此了。相信可能很多人也会有和我类似的想法,是否也都曾迷茫过?幸运的是,伴随着对前端的接触和深入,云雾散开。前端组
如何安装JavaFX
dingdingfish
JavaJavaJavaFX
JavaFX的官方网站在这里,从JDK11开始,javaFX未包含在JDK中。安装过程如下:安装JDK,本例为JDK11,下载地址。下载JavaFX11,下载地址。安装JavaFX11首先找到当前SDK的路径->/usr/java/jdk-11.0.4:#whichjavac/bin/javac#ls-ljavaclrwxrwxrwx.1rootroot23Aug1911:09javac->/et
JavaSE的集合(Collection)
pkhlll
java
集合主要分为两大系列:Collection和MapCollection:Collection的子接口有Set、List、QueueCollection是层次结构的根接口,是所有单列集合的父接口,在Collection中定义了单列集合(List和Set)的通用的一些方法:1、添加元素(1)add(Eobj):添加元素对象到当前集合中(2)addAll(Collectionother):添加other
排序的艺术:Spring Data JPA 如何玩转关联实体排序 (. 运算符的奥秘) ✨
小丁学Java
SpringDataJPAjpa
这次我们来深入探讨SpringDataJPA分页排序中一个非常实用但又容易混淆的技巧:如何优雅地对关联实体(或嵌套属性)进行排序。排序的艺术:SpringDataJPA如何玩转关联实体排序(.运算符的奥秘)你好,我是坚持哥!在构建Web应用时,分页查询是家常便饭。SpringDataJPA(JavaPersistenceAPI)提供了强大的Pageable接口,让分页和排序变得异常简单。但当你的排
【2025B卷专题】华为OD机试2025B卷统一考试题库清单,时间紧张就刷这个
专栏导读本专栏收录于《华为OD机试(JAVA)真题(B卷+A卷+C卷+D卷+E卷)》。刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新,全天CSDN在线答疑。2025年5月12日,华为官方已经将华为OD机试(A卷)切换为B卷。目前正在考的是B卷,按照华
【全网首发】华为OD机试 2025B卷 机考真题库清单(全真题库)含考点说明
哪 吒
搬砖工逆袭Java架构师华为odjava2025B卷华为OD机试
专栏导读本专栏收录于《华为OD机试(JAVA)真题(E卷+D卷+A卷+B卷+C卷)》。刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新,全天CSDN在线答疑。2025年5月12日,华为官方已经将华为OD机试(A卷)切换为B卷。目前正在考的是B卷,按照华
【2025B卷首发】华为OD机试真题+全流程解析+备考攻略+经验分享+Java最佳实现
专栏导读本专栏收录于《华为OD机试(JAVA)真题(E卷+D卷+A卷+B卷+C卷)》。刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新,全天CSDN在线答疑。2025年5月12日,华为官方已经将华为OD机试(A卷)切换为B卷。目前正在考的是B卷,按照华
后端领域的自然语言处理技术应用
大厂资深架构师
SpringBoot开发实战自然语言处理easyui人工智能ai
后端领域的自然语言处理技术应用关键词:后端领域、自然语言处理、技术应用、算法原理、实际案例摘要:本文聚焦于后端领域中自然语言处理技术的应用。首先介绍了相关背景,包括目的范围、预期读者等。接着阐述核心概念与联系,通过文本示意图和Mermaid流程图展示其原理和架构。详细讲解了核心算法原理并给出Python源代码示例,同时介绍了数学模型和公式。通过项目实战,展示代码实际案例并进行详细解释。分析了自然语
Conda安装与使用
目录一、软件安装及conda管理1.conda下载2.miniconda安装二、环境配置1.配置镜像:2.创建环境、移除环境:3.查看小环境4.进入、退出小环境5.查找并安装软件三、一步到位其他:参考资料:一、软件安装及conda管理conda可以来管理大量的生物信息学软件,或者想要复现一些文章中的实验结果需要不同环境的切换。1.conda下载(1)anacondaanaconda|镜像站使用帮助
java 同步redis到mysql_Yii2 redis同步数据到mysql
兰艳知己
java同步redis到mysql
将redis数据写入mysql中:本次案例讲解将如何将商城中商品浏览次数通过缓存记录并写入mysql中具体的redis安装过程暂且就省略了.....一、安装redis插件|配置rediscomposerrequireyiisoft/yii2-redis找到common的config文件,在components下加入redis配置参数'redis'=>['class'=>'yii\redis\Con
linux环境下tomcat安装
M.za
linuxtomcat运维服务器
Tomcat一、什么是Tomcat?1.1、Tomcat介绍Tomcat又叫ApacheTomcat最早是sun公司开发的,1999年捐献给apache基金会,隶属于雅加达项目,现在已经独立成一个顶级项目,因为tomcat技术先进,性能稳定,又是一个开源的web应用服务器,所以很多企业都在使用,很多Java开发者也在使用,开发调试jsp的首选,被更多企业用于Java容器。Tomcat官网:http
redis做同步或异步队列
瞧着不像好人呐
redisredisjava数据库
redis实现队列主要是使用数据结构中的list,相当于Java中的ArrayList因为它是按照塞入顺序排序的结构,我们就可以按照左边塞入,右边取出的方式来实现先入先出的队列需求。publicvoidrpush(Stringkey,Stringvalue){Jedisjedis=null;try{jedis=jedisPool.getResource();jedis.rpush(key,valu
企业内网系统:从传统开发到智能赋能的进化之路
飞算JavaAI开发助手
科技人工智能大数据java
在当今数字化浪潮中,企业内网系统作为支撑日常运营的核心基础设施,其开发效率与质量直接关系到企业的竞争力。传统开发模式下,程序员需要手动完成需求分析、架构设计、代码编写、测试调试等全流程工作,不仅耗时费力,还容易因人为疏忽导致质量隐患。而随着人工智能技术的突破性进展,以飞算JavaAI为代表的智能开发工具正在重塑企业内网系统的开发范式,为程序员提供从设计到落地的全链路智能支持。一、传统企业内网系统开
钉钉企业应用开发系列:前端实现钉钉扫码登录功能
脑袋大大的
钉钉生态创业者专栏钉钉前端第三方登录
本文将围绕“钉钉扫码登录”这一功能点展开讲解,并结合前端技术栈(HTML+JavaScript+Vue3)进行实现。我们将通过调用钉钉开放平台提供的JSAPI来实现扫码登录的功能,并展示完整的代码示例。一、前置准备1.注册钉钉开发者账号并创建企业应用访问钉钉开放平台。创建一个企业内部应用或第三方企业应用。获取corpId和redirect_uri等信息,用于后续配置。2.获取扫码登录权限确保你的应
从实验到文化 - “混沌日”与持续混沌
weixin_42587823
混沌数据库混沌
从实验到文化-“混沌日”与持续混沌第一部分:锻炼团队的“免疫系统”-混沌日(GameDay)什么是“混沌日”?混沌日是一场有计划、有组织的演习活动。在活动中,团队成员们齐聚一堂(无论是线上还是线下),在一个受控的环境中(理想情况是生产环境,但从预生产环境开始是更安全的选择),主动触发一次模拟的真实故障场景。它就像一次针对技术团队和系统的消防演习。它的价值何在?混沌实验不仅仅测试机器,它同样也测试人
Java基础学习笔记2
qichi333
学习笔记javaeclipse
今天是Java基础学习第二天,加油!!!下面是我今天记的一些笔记。(有点懒惰了,爬虫今天没学,因为赖床了(bushi),但我会勤奋起来的^_^,一定一定!明天不能偷懒了天!!)一、运算符例子:inta=10;intb=20;intc=a+b;其中,“+”是运算符,且是算术运算符;“a+b”是表达式,且是算术表达式。1.算术运算符例1:publicclassdemo3{publicstaticvoi
Spring框架中的Component与Bean注解
SpringBoot中的@Bean与@ComponentSpring的@Component和@Bean注解的关键区别在于:@Bean注解可用于暴露您自己编写的JavaBeans,而@Component注解可用于暴露源代码由他人维护的JavaBeans。Sprin
量子计算的数学地基:解码希尔伯特空间的魔法
牧之112
量子计算
在科技圈,“量子计算”早已不是陌生的名词。从谷歌的“量子霸权”实验到IBM的量子云服务,从药物研发的分子模拟到密码学的革命性突破,量子计算正以颠覆式的姿态重塑着人类对计算的认知。但在这些令人惊叹的应用背后,藏着一个关键的数学基石——希尔伯特空间(HilbertSpace)。它像一片隐形的“量子舞台”,支撑着量子比特的叠加、纠缠与计算,是理解量子计算本质绕不开的概念。一、从“普通空间”到“量子空间”
JavaScript中的系统对话框:alert、confirm、prompt
JavaScript中的系统对话框:alert、confirm、prompt在Web开发的世界里,JavaScript始终扮演着“桥梁”的角色——它连接用户与网页,让静态的页面焕发活力。而在这座桥梁上,系统对话框(SystemDialogs)是最基础却最实用的工具之一。它们像是一位贴心的助手,在用户需要确认、提示或输入时,悄然出现,又在任务完成后无声退场。今天,我们就来聊聊JavaScript中三
Go内存压力测试:模拟与应对高负载
Go高并发架构_王工
golang压力测试后端
一、引言在当今微服务架构和云原生应用盛行的时代,Go语言凭借其出色的并发处理能力和较低的资源消耗,成为构建高性能后端服务的首选语言之一。然而,随着业务规模的扩大和用户量的增长,我们的服务经常会面临突如其来的流量高峰和持续的高负载挑战。就像一辆汽车需要在极端条件下测试其性能极限一样,我们的Go应用也需要在上线前经受住内存压力测试的洗礼。这不仅能帮助我们发现潜在的内存泄漏和性能瓶颈,还能确保系统在高负
Nginx中如何配置WebSocket代理?
m0_74824025
面试学习路线阿里巴巴nginxwebsocket运维
Nginx可以配置为WebSocket代理,将WebSocket连接从客户端转发到后端服务器。以下是如何在Nginx中配置WebSocket代理的详细步骤和示例配置。1.安装Nginx确保你已经安装了Nginx。如果没有安装,可以使用以下命令进行安装:sudoapt-getupdatesudoapt-getinstallnginx2.配置WebSocket代理编辑Nginx配置文件,通常位于/et
SpringBoot+AOP+自定义注解,实现日志记录
一.定义自定义注解importjava.lang.annotation.*;/***@authorawen*定义注解目的想让他当作切点*/@Target({ElementType.METHOD})@Retention(RetentionPolicy.RUNTIME)//.java.class字节码@Documentedpublic@interfaceLog{/***处理类型**@return{@l
xml解析
小猪猪08
xml
1、DOM解析的步奏
准备工作:
1.创建DocumentBuilderFactory的对象
2.创建DocumentBuilder对象
3.通过DocumentBuilder对象的parse(String fileName)方法解析xml文件
4.通过Document的getElem
每个开发人员都需要了解的一个SQL技巧
brotherlamp
linuxlinux视频linux教程linux自学linux资料
对于数据过滤而言CHECK约束已经算是相当不错了。然而它仍存在一些缺陷,比如说它们是应用到表上面的,但有的时候你可能希望指定一条约束,而它只在特定条件下才生效。
使用SQL标准的WITH CHECK OPTION子句就能完成这点,至少Oracle和SQL Server都实现了这个功能。下面是实现方式:
CREATE TABLE books (
id &
Quartz——CronTrigger触发器
eksliang
quartzCronTrigger
转载请出自出处:http://eksliang.iteye.com/blog/2208295 一.概述
CronTrigger 能够提供比 SimpleTrigger 更有具体实际意义的调度方案,调度规则基于 Cron 表达式,CronTrigger 支持日历相关的重复时间间隔(比如每月第一个周一执行),而不是简单的周期时间间隔。 二.Cron表达式介绍 1)Cron表达式规则表
Quartz
Informatica基础
18289753290
InformaticaMonitormanagerworkflowDesigner
1.
1)PowerCenter Designer:设计开发环境,定义源及目标数据结构;设计转换规则,生成ETL映射。
2)Workflow Manager:合理地实现复杂的ETL工作流,基于时间,事件的作业调度
3)Workflow Monitor:监控Workflow和Session运行情况,生成日志和报告
4)Repository Manager:
linux下为程序创建启动和关闭的的sh文件,scrapyd为例
酷的飞上天空
scrapy
对于一些未提供service管理的程序 每次启动和关闭都要加上全部路径,想到可以做一个简单的启动和关闭控制的文件
下面以scrapy启动server为例,文件名为run.sh:
#端口号,根据此端口号确定PID
PORT=6800
#启动命令所在目录
HOME='/home/jmscra/scrapy/'
#查询出监听了PORT端口
人--自私与无私
永夜-极光
今天上毛概课,老师提出一个问题--人是自私的还是无私的,根源是什么?
从客观的角度来看,人有自私的行为,也有无私的
Ubuntu安装NS-3 环境脚本
随便小屋
ubuntu
将附件下载下来之后解压,将解压后的文件ns3environment.sh复制到下载目录下(其实放在哪里都可以,就是为了和我下面的命令相统一)。输入命令:
sudo ./ns3environment.sh >>result
这样系统就自动安装ns3的环境,运行的结果在result文件中,如果提示
com
创业的简单感受
aijuans
创业的简单感受
2009年11月9日我进入a公司实习,2012年4月26日,我离开a公司,开始自己的创业之旅。
今天是2012年5月30日,我忽然很想谈谈自己创业一个月的感受。
当初离开边锋时,我就对自己说:“自己选择的路,就是跪着也要把他走完”,我也做好了心理准备,准备迎接一次次的困难。我这次走出来,不管成败
如何经营自己的独立人脉
aoyouzi
如何经营自己的独立人脉
独立人脉不是父母、亲戚的人脉,而是自己主动投入构造的人脉圈。“放长线,钓大鱼”,先行投入才能产生后续产出。 现在几乎做所有的事情都需要人脉。以银行柜员为例,需要拉储户,而其本质就是社会人脉,就是社交!很多人都说,人脉我不行,因为我爸不行、我妈不行、我姨不行、我舅不行……我谁谁谁都不行,怎么能建立人脉?我这里说的人脉,是你的独立人脉。 以一个普通的银行柜员
JSP基础
百合不是茶
jsp注释隐式对象
1,JSP语句的声明
<%! 声明 %> 声明:这个就是提供java代码声明变量、方法等的场所。
表达式 <%= 表达式 %> 这个相当于赋值,可以在页面上显示表达式的结果,
程序代码段/小型指令 <% 程序代码片段 %>
2,JSP的注释
<!-- -->
web.xml之session-config、mime-mapping
bijian1013
javaweb.xmlservletsession-configmime-mapping
session-config
1.定义:
<session-config>
<session-timeout>20</session-timeout>
</session-config>
2.作用:用于定义整个WEB站点session的有效期限,单位是分钟。
mime-mapping
1.定义:
<mime-m
互联网开放平台(1)
Bill_chen
互联网qq新浪微博百度腾讯
现在各互联网公司都推出了自己的开放平台供用户创造自己的应用,互联网的开放技术欣欣向荣,自己总结如下:
1.淘宝开放平台(TOP)
网址:http://open.taobao.com/
依赖淘宝强大的电子商务数据,将淘宝内部业务数据作为API开放出去,同时将外部ISV的应用引入进来。
目前TOP的三条主线:
TOP访问网站:open.taobao.com
ISV后台:my.open.ta
【MongoDB学习笔记九】MongoDB索引
bit1129
mongodb
索引
可以在任意列上建立索引
索引的构造和使用与传统关系型数据库几乎一样,适用于Oracle的索引优化技巧也适用于Mongodb
使用索引可以加快查询,但同时会降低修改,插入等的性能
内嵌文档照样可以建立使用索引
测试数据
var p1 = {
"name":"Jack",
"age&q
JDBC常用API之外的总结
白糖_
jdbc
做JAVA的人玩JDBC肯定已经很熟练了,像DriverManager、Connection、ResultSet、Statement这些基本类大家肯定很常用啦,我不赘述那些诸如注册JDBC驱动、创建连接、获取数据集的API了,在这我介绍一些写框架时常用的API,大家共同学习吧。
ResultSetMetaData获取ResultSet对象的元数据信息
apache VelocityEngine使用记录
bozch
VelocityEngine
VelocityEngine是一个模板引擎,能够基于模板生成指定的文件代码。
使用方法如下:
VelocityEngine engine = new VelocityEngine();// 定义模板引擎
Properties properties = new Properties();// 模板引擎属
编程之美-快速找出故障机器
bylijinnan
编程之美
package beautyOfCoding;
import java.util.Arrays;
public class TheLostID {
/*编程之美
假设一个机器仅存储一个标号为ID的记录,假设机器总量在10亿以下且ID是小于10亿的整数,假设每份数据保存两个备份,这样就有两个机器存储了同样的数据。
1.假设在某个时间得到一个数据文件ID的列表,是
关于Java中redirect与forward的区别
chenbowen00
javaservlet
在Servlet中两种实现:
forward方式:request.getRequestDispatcher(“/somePage.jsp”).forward(request, response);
redirect方式:response.sendRedirect(“/somePage.jsp”);
forward是服务器内部重定向,程序收到请求后重新定向到另一个程序,客户机并不知
[信号与系统]人体最关键的两个信号节点
comsci
系统
如果把人体看做是一个带生物磁场的导体,那么这个导体有两个很重要的节点,第一个在头部,中医的名称叫做 百汇穴, 另外一个节点在腰部,中医的名称叫做 命门
如果要保护自己的脑部磁场不受到外界有害信号的攻击,最简单的
oracle 存储过程执行权限
daizj
oracle存储过程权限执行者调用者
在数据库系统中存储过程是必不可少的利器,存储过程是预先编译好的为实现一个复杂功能的一段Sql语句集合。它的优点我就不多说了,说一下我碰到的问题吧。我在项目开发的过程中需要用存储过程来实现一个功能,其中涉及到判断一张表是否已经建立,没有建立就由存储过程来建立这张表。
CREATE OR REPLACE PROCEDURE TestProc
IS
fla
为mysql数据库建立索引
dengkane
mysql性能索引
前些时候,一位颇高级的程序员居然问我什么叫做索引,令我感到十分的惊奇,我想这绝不会是沧海一粟,因为有成千上万的开发者(可能大部分是使用MySQL的)都没有受过有关数据库的正规培训,尽管他们都为客户做过一些开发,但却对如何为数据库建立适当的索引所知较少,因此我起了写一篇相关文章的念头。 最普通的情况,是为出现在where子句的字段建一个索引。为方便讲述,我们先建立一个如下的表。
学习C语言常见误区 如何看懂一个程序 如何掌握一个程序以及几个小题目示例
dcj3sjt126com
c算法
如果看懂一个程序,分三步
1、流程
2、每个语句的功能
3、试数
如何学习一些小算法的程序
尝试自己去编程解决它,大部分人都自己无法解决
如果解决不了就看答案
关键是把答案看懂,这个是要花很大的精力,也是我们学习的重点
看懂之后尝试自己去修改程序,并且知道修改之后程序的不同输出结果的含义
照着答案去敲
调试错误
centos6.3安装php5.4报错
dcj3sjt126com
centos6
报错内容如下:
Resolving Dependencies
--> Running transaction check
---> Package php54w.x86_64 0:5.4.38-1.w6 will be installed
--> Processing Dependency: php54w-common(x86-64) = 5.4.38-1.w6 for
JSONP请求
flyer0126
jsonp
使用jsonp不能发起POST请求。
It is not possible to make a JSONP POST request.
JSONP works by creating a <script> tag that executes Javascript from a different domain; it is not pos
Spring Security(03)——核心类简介
234390216
Authentication
核心类简介
目录
1.1 Authentication
1.2 SecurityContextHolder
1.3 AuthenticationManager和AuthenticationProvider
1.3.1 &nb
在CentOS上部署JAVA服务
java--hhf
javajdkcentosJava服务
本文将介绍如何在CentOS上运行Java Web服务,其中将包括如何搭建JAVA运行环境、如何开启端口号、如何使得服务在命令执行窗口关闭后依旧运行
第一步:卸载旧Linux自带的JDK
①查看本机JDK版本
java -version
结果如下
java version "1.6.0"
oracle、sqlserver、mysql常用函数对比[to_char、to_number、to_date]
ldzyz007
oraclemysqlSQL Server
oracle &n
记Protocol Oriented Programming in Swift of WWDC 2015
ningandjin
protocolWWDC 2015Swift2.0
其实最先朋友让我就这个题目写篇文章的时候,我是拒绝的,因为觉得苹果就是在炒冷饭, 把已经流行了数十年的OOP中的“面向接口编程”还拿来讲,看完整个Session之后呢,虽然还是觉得在炒冷饭,但是毕竟还是加了蛋的,有些东西还是值得说说的。
通常谈到面向接口编程,其主要作用是把系统��设计和具体实现分离开,让系统的每个部分都可以在不影响别的部分的情况下,改变自身的具体实现。接口的设计就反映了系统
搭建 CentOS 6 服务器(15) - Keepalived、HAProxy、LVS
rensanning
keepalived
(一)Keepalived
(1)安装
# cd /usr/local/src
# wget http://www.keepalived.org/software/keepalived-1.2.15.tar.gz
# tar zxvf keepalived-1.2.15.tar.gz
# cd keepalived-1.2.15
# ./configure
# make &a
ORACLE数据库SCN和时间的互相转换
tomcat_oracle
oraclesql
SCN(System Change Number 简称 SCN)是当Oracle数据库更新后,由DBMS自动维护去累积递增的一个数字,可以理解成ORACLE数据库的时间戳,从ORACLE 10G开始,提供了函数可以实现SCN和时间进行相互转换;
用途:在进行数据库的还原和利用数据库的闪回功能时,进行SCN和时间的转换就变的非常必要了;
操作方法: 1、通过dbms_f
Spring MVC 方法注解拦截器
xp9802
spring mvc
应用场景,在方法级别对本次调用进行鉴权,如api接口中有个用户唯一标示accessToken,对于有accessToken的每次请求可以在方法加一个拦截器,获得本次请求的用户,存放到request或者session域。
python中,之前在python flask中可以使用装饰器来对方法进行预处理,进行权限处理
先看一个实例,使用@access_required拦截:
?