【数据结构第三章】- 栈

目录

一、栈的定义和特点

二、顺序栈的表示和实现

2.1 - SeqStack.h

2.2 - SeqStack.c

2.3 - test.c

三、链栈的表示和实现

3.1 - LinkStack.h

3.2 - LinkStack.c

3.3 - test.c

---

 

---

一、栈的定义和特点

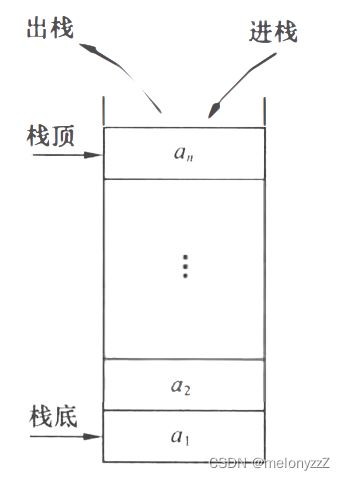
栈（stack）是限定仅在表尾进行插入或删除操作的线性表。因此，对栈来说，表尾端有其特殊含义，称为栈顶（top），相应地，表头端称为栈底（bottom）。不含元素的空表称为空栈。

假设栈 S = (a1, a2, ..., an)，则称 a1 为栈底元素，an 为栈顶元素。栈中元素按照 a1, a2, ..., an 的次序进栈，退栈的第一个元素应为栈顶元素。换句话说，栈的修改是按后进先出的原则进行，如下图所示。因此，栈又称为后进先出（Last In First Out, LIFO）的线性表。

 

栈的插入操作叫做进栈/压栈/入栈；栈的删除操作叫做出栈。

在日常生活中，还要很多类似栈的例子。例如，洗干净的盘子总是逐个往上叠好放在已经洗好的盘子上面，而用时从上往下逐个取用。栈的特点正是上述实际应用的抽象。在程序设计中，如果需要按照保存数据时相反的顺序来使用数据，则可以利用栈来实现。

 

 

---

二、顺序栈的表示和实现

顺序栈是指利用顺序存储结构实现的栈，即利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素。动态顺序栈的定义如下：

typedef struct SeqStack
{
    DataType* data;
    int top;
    int capacity;
}SeqStack;

 

2.1 - SeqStack.h

#pragma once

#include 

// 动态顺序栈
#define DEFAULT_CAPACITY 5  // 默认最大容量

typedef int DataType;

typedef struct SeqStack
{
	DataType* data;
	int top;
	int capacity;
}SeqStack;

// 基本操作
void SeqStackInit(SeqStack* pss);  // 初始化

bool SeqStackEmpty(const SeqStack* pss);  // 判断是否为空栈

void SeqStackPush(SeqStack* pss, DataType e);  // 入栈
void SeqStackPop(SeqStack* pss);  // 出栈

DataType SeqStackTop(const SeqStack* pss);  // 返回栈顶元素  

int SeqStackSize(const SeqStack* pss);  // 返回栈的有效元素个数

void SeqStackDestroy(SeqStack* pss);  // 销毁

 

2.2 - SeqStack.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "SeqStack.h"
#include 
#include 

// 初始化
void SeqStackInit(SeqStack* pss)
{
	assert(pss);
	pss->data = (DataType*)malloc(sizeof(DataType) * DEFAULT_CAPACITY);
	if (NULL == pss->data)
	{
		perror("initialization failed!");
		exit(-1);
	}
	pss->top = 0;
	pss->capacity = DEFAULT_CAPACITY;
}


// 判断是否为空栈
bool SeqStackEmpty(const SeqStack* pss)
{
	assert(pss);
	return pss->top == 0;  // 若为空栈，返回 true，否则返回 false
}


// 入栈
void SeqStackPush(SeqStack* pss, DataType e)
{
	assert(pss);
	// 判断是否需要扩容
	if (pss->top == pss->capacity)
	{
		DataType* tmp = (DataType*)realloc(pss->data, sizeof(DataType) * 2 * pss->capacity);
		if (NULL == tmp)
		{
			perror("realloc failed!");
			return;
		}
		pss->data = tmp;
		pss->capacity *= 2;
	}
	// 入栈
	pss->data[pss->top++] = e;
}


// 出栈
void SeqStackPop(SeqStack* pss)
{
	assert(pss);
	assert(!SeqStackEmpty(pss));  // 前提是栈非空
	// 出栈
	--pss->top;
}


// 返回栈顶元素
DataType SeqStackTop(const SeqStack* pss)
{
	assert(pss);
	assert(!SeqStackEmpty(pss));  // 前提是栈非空
	return pss->data[pss->top - 1];
}


// 返回栈的有效元素个数
int SeqStackSize(const SeqStack* pss)
{
	assert(pss);
	return pss->top;
}


// 销毁
void SeqStackDestroy(SeqStack* pss)
{
	assert(pss);
	free(pss->data);
	pss->data = NULL;
	pss->top = 0;
	pss->capacity = DEFAULT_CAPACITY;
}

 

2.3 - test.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "SeqStack.h"
#include 

int main()
{
	SeqStack s;
	// 初始化
	SeqStackInit(&s);  
	// 入栈：1 2 3 4
	SeqStackPush(&s, 1);
	SeqStackPush(&s, 2);
	SeqStackPush(&s, 3);
	SeqStackPush(&s, 4);
	printf("当前栈中有效元素个数为：%d\n", SeqStackSize(&s));  // 4
	// 出栈：4 3 2 1
	while (!SeqStackEmpty(&s))
	{
		printf("%d ", SeqStackTop(&s));
		SeqStackPop(&s);
	}
	printf("\n");
	// 销毁
	SeqStackDestroy(&s);
}

 

 

---

三、链栈的表示和实现

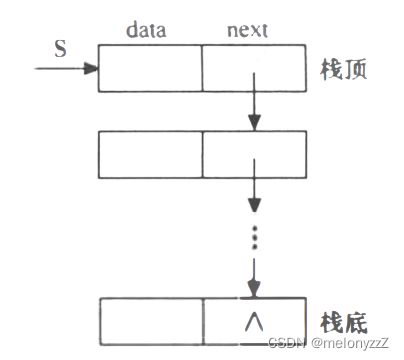
链栈是指采用链式存储结构实现的栈。通常链栈用单链表来表示，如下图所示。

 

由于栈的主要操作是在栈顶插入和删除，显然以链表的头部作为栈顶是最方便的。

链栈的定义如下：

typedef struct StackNode
{
    DataType data;
    struct StackNode* next;
}StackNode, *LinkStack;

 

3.1 - LinkStack.h

#pragma once

#include 
#include 

// 链栈
typedef int DataType;

typedef struct StackNode
{
	DataType data;
	struct StackNode* next;
}StackNode, *LinkStack;

// 基本操作
void LinkStackInit(LinkStack* pphead);  // 初始化

bool LinkStackEmpty(const LinkStack phead);  // 判断是否为空栈

void LinkStackPush(LinkStack* pphead, DataType e);  // 入栈
void LinkStackPop(LinkStack* pphead);  // 出栈

DataType LinkStackTop(const LinkStack phead);  // 返回栈顶元素

int LinkStackSize(const LinkStack phead);  // 返回栈的有效元素个数

void LinkStackDestroy(LinkStack* pphead);  // 销毁

 

3.2 - LinkStack.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "LinkStack.h"
#include 
#include 

// 初始化
void LinkStackInit(LinkStack* pphead)
{
	assert(pphead);
	*pphead = NULL;
}


// 判断是否为空栈
bool LinkStackEmpty(const LinkStack phead)
{
	return phead == NULL;
}


// 入栈
void LinkStackPush(LinkStack* pphead, DataType e)
{
	assert(pphead);
	StackNode* newnode = (StackNode*)malloc(sizeof(StackNode));
	if (NULL == newnode)
	{
		perror("malloc failed!");
		return;
	}
	newnode->data = e;
	newnode->next = *pphead;  // 将新结点插入栈顶
	*pphead = newnode;  // 修改头指针
}


// 出栈
void LinkStackPop(LinkStack* pphead)
{
	assert(pphead);
	assert(!LinkStackEmpty(*pphead));  // 前提是栈非空
	StackNode* tmp = *pphead;
	*pphead = (*pphead)->next;
	free(tmp);
}


// 返回栈顶元素
DataType LinkStackTop(const LinkStack phead)
{
	assert(!LinkStackEmpty(phead));  // 前提是栈非空
	return phead->data;
}


// 返回栈的有效元素个数
int LinkStackSize(const LinkStack phead)
{
	const StackNode* cur = phead;
	int sz = 0;
	while (cur != NULL)
	{
		++sz;
		cur = cur->next;
	}
	return sz;
}


// 销毁
void LinkStackDestroy(LinkStack* pphead)
{
	StackNode* cur = *pphead;
	while (cur != NULL)
	{
		StackNode* tmp = cur;
		cur = cur->next;
		free(tmp);
	}
	*pphead = NULL;
}

 

3.3 - test.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "LinkStack.h"

int main()
{
	LinkStack phead;
	// 初始化
	LinkStackInit(&phead);  
	// 入栈：1 2 3 4
	LinkStackPush(&phead, 1);
	LinkStackPush(&phead, 2);
	LinkStackPush(&phead, 3);
	LinkStackPush(&phead, 4);
	printf("当前栈中有效元素个数为：%d\n", LinkStackSize(phead));  // 4
	// 出栈：4 3 2 1
	while (!LinkStackEmpty(phead))
	{
		printf("%d ", LinkStackTop(phead));
		LinkStackPop(&phead);
	}
	printf("\n");
	// 销毁
	LinkStackDestroy(&phead);
	return 0;
}