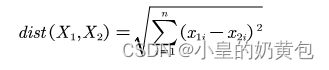Python实现最近邻数自动寻优的KNN算法

目录

摘要

0 绪论

1 材料准备

2 算法原理

3 算法实现

4 结论

5 备注

摘要

        KNN算法是一种传统的机器学习算法，在数学建模、数据挖掘和数据分析竞赛中也是常用的算法之一，网上的实现方法基本都是将最近邻数（n_neighbors）设为一个固定值，但实际上，这个n_neighbors是并不一定是最优的，所以，本文在这个背景下，在n_neighbors ∈ [1 , 11]中执行自动寻优，并将最优组合进行KNN算法的拟合，并利用混淆矩阵和F1-Score进行模型评估。

0 绪论

        在机器学习算法中，算法的实现固然重要，但是一次较为合理的数据预处理也是至关重要的，甚至对后续算法的精确率和预测都有很大的影响。本文仅对KNN算法的实现进行详细的说明，至于数据预处理，笔者默认所有读者已将你手上的数据完成了数据预处理部分。

        n_neighbors 是 KNN 算法中的一个参数，它指定了 KNN 算法使用的最近邻数。在 KNN 算法中，当你想要预测一个样本的类别时，会在训练数据中找到与该样本最近的 n 个样本（这些样本称为“最近邻”）。然后会使用这些最近邻的类别来预测该样本的类别。
        n_neighbors 就是指 KNN 算法使用的最近邻数。如果你将 n_neighbors 设为 5，则 KNN 算法会在训练数据中找到与待预测样本最近的 5 个样本，并使用这些样本的类别来预测待预测样本的类别。
        KNN 算法的 n_neighbors 参数越大，则会使用的最近邻样本数越多，这意味着预测的类别可能会受到更多样本的影响。因此，n_neighbors 越大时，预测的类别可能会变得更加稳定，但是模型的泛化能力可能会下降。

1 材料准备

        Python编译器：Pycharm社区版或个人版等

        数据准备：本文使用2022年数维杯国际大学生数学建模竞赛C题的附件数据为例。

        数据预处理：本文所使用的数据，已通过初步的数据清洗、异常值处理、空缺值处理、特征编码、相关性分析降维和决策树特征重要性二次特征降维等操作，得到‘CDRSB_bl’，'PIB_bl'，'FBB_bl'三个自变量特征，以及'DX_bl'目标特征。

2 算法原理

        KNN分类的过程主要是基于样本之间的距离比较，即需要从训练样本中找出K个与其最相近的样本，然后通过比较K个样本中所属类别个数的多少来判定测试样本的类别。KNN算法需要决定K的取值，K的取值不一样，也有可能对诊断的结果造成影响，因此，在本文主要采用欧式距离作为样本距离的度量。具体计算公式如下：

                        

        其中，dist(X1,X2)表示训练样本中两个对象之间的距离，距离越近表示两个对象越相似，x1i，x2i分别表示X1，X2第个属性值。

3 算法实现

        3.1 数据加载        

import numpy as np
import pandas as pd
# 加载数据
X = pd.DataFrame(pd.read_excel('DataX.xlsx')).values  # 输入特征
y = pd.DataFrame(pd.read_excel('DataY.xlsx')).values  # 目标变量
y = np.ravel(y)  # KNN算法要求目标变量是一位数组，利用numpy的ravel()函数进行转换

        此处将自变量特征存放在DataX.xlsx中，目标变量特征存放在DataY中，机器学习算法的目标变量限制为一维数据，所以此处用了numpy的ravel函数进行转化，避免没必要的错误和警告。

        如果比赛中需要对附加数据进行预测，可以存放在另一个文件中，格式与DataX.xlsx一致，利用predict函数进行预测即可。

        3.2 将数据集分为训练集和测试集

from sklearn.model_selection import train_test_split
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, train_size=0.7, random_state=42)

        此处将训练数据设为0.7，测试数据设为0.3，如需进行敏感性分析或稳定性分析，可适当调整训练测试数据占比。

        3.3 使用 GridSearchCV 对象进行自动寻优

from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsClassifier

# 创建 KNN 分类器
knn = KNeighborsClassifier()

# 定义要尝试的 n_neighbors 参数的取值范围
param_grid = {'n_neighbors': range(1, 11)}

# 创建 GridSearchCV 对象
grid_search = GridSearchCV(knn, param_grid, cv=5)

# 使用 GridSearchCV 对象进行自动寻优
grid_search.fit(X, y)

# 输出最优的参数组合
print(grid_search.best_params_)

        GridSearchCV 类可以自动尝试多种参数组合，并使用交叉验证来评估每组参数的性能。我们使用了交叉验证，每组参数尝试了 5 次，所以一共尝试了 5 * 10 = 50 种参数组合。最后，GridSearchCV 类会自动选择性能最优的参数组合。

        3.4 创建 KNN 分类器并训练模型

t = grid_search.best_params_['n_neighbors']
# 创建 KNN 分类器并训练模型
knn = KNeighborsClassifier(n_neighbors=t)
knn.fit(X_train, y_train)

        3.5 评估模型

# 在测试集上评估模型
y_pred = knn.predict(X_test)
#  输出结果分布矩阵
print(confusion_matrix(y_test, y_pred))
print("Accuracy:")
print(accuracy_score(y_test, y_pred))
# 输出混淆矩阵、F1-score 和精确率
print("Classification Report:")
print(classification_report(y_test, y_pred))

        一个分类器的好坏，需要通过混淆矩阵或F1-Score进行评估，此处都进行了输出，模型的混淆矩阵、F1-Score和精确率，都是用来做模型评估使用的。

        最好就是通过对比多个算法的F1-Score和精确率，说明你们团队选择KNN算法或其他算法的理由，一般来说，这一步是不可或缺的。

        3.6 完整实现代码

import numpy as np
import pandas as pd
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
from sklearn.model_selection import train_test_split

# 加载数据
X = pd.DataFrame(pd.read_excel('DataX.xlsx')).values  # 输入特征
y = pd.DataFrame(pd.read_excel('DataY.xlsx')).values  # 目标变量
y = np.ravel(y)  # KNN算法要求目标变量是一位数组，利用numpy的ravel()函数进行转换

# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, train_size=0.7, random_state=42)

from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsClassifier

# 创建 KNN 分类器
knn = KNeighborsClassifier()

# 定义要尝试的 n_neighbors 参数的取值范围
param_grid = {'n_neighbors': range(1, 11)}

# 创建 GridSearchCV 对象
grid_search = GridSearchCV(knn, param_grid, cv=5)

# 使用 GridSearchCV 对象进行自动寻优
grid_search.fit(X, y)

# 输出最优的参数组合
print(grid_search.best_params_)
t = grid_search.best_params_['n_neighbors']
# 创建 KNN 分类器并训练模型
knn = KNeighborsClassifier(n_neighbors=t)
knn.fit(X_train, y_train)

# 在测试集上评估模型
y_pred = knn.predict(X_test)
#  输出结果分布矩阵
print(confusion_matrix(y_test, y_pred))
print("Accuracy:")
print(accuracy_score(y_test, y_pred))
# 输出混淆矩阵、F1-score 和精确率
print("Classification Report:")
print(classification_report(y_test, y_pred))

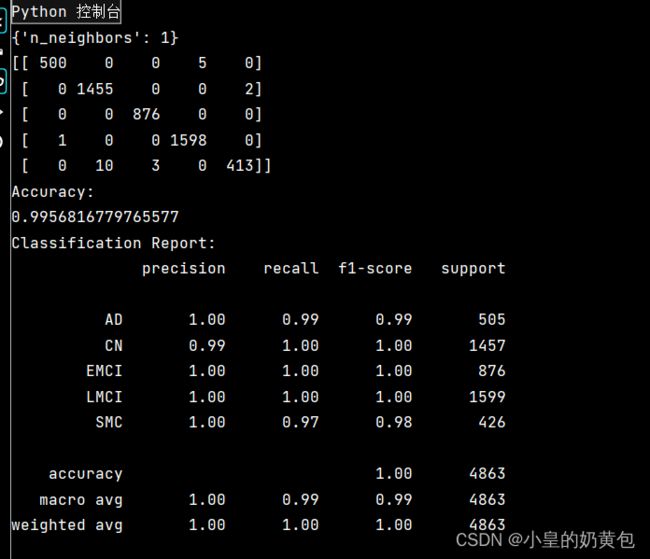
        3.7 样例输出

         上图是笔者的数据进行KNN算法所得到的输出样例，无论是精确率、召回率还是F1-Score，都是非常出色的，说明这个模型的拟合是优秀的。

4 结论

        利用Python进行自动寻优，实现KNN算法全过程，读者可在本示例中进行拓展，进行适应性调整，完成后续的竞赛。

5 备注

        本文为原创文章，禁止转载，违者必究。