HMM学习(2)-Generating Patterns

原文http://blog.csdn.net/yihucha166/archive/2007/12/17/1943774.aspx

2. Generating Patterns

2.1 Deterministic Patterns（确定性的模式）

Consider a set of traffic lights; the sequence of lights is red - red/amber - green - amber - red. The sequence can be pictured as a state machine, where the different states of the traffic lights follow each other.

考虑一个交通灯（红绿灯）的集合；灯的序列是 红 – 红和黄褐色 – 绿 – 黄褐色 – 红。这个序列可以画成一个状态机，其中交通灯的不同状态彼此更替。

e.g.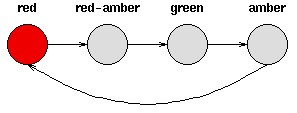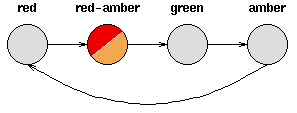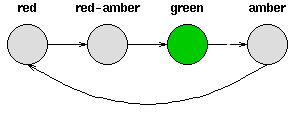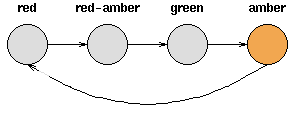

Notice that each state is dependent solely on the previous state, so if the lights are green, an amber light will always follow - that is, the system is deterministic. Deterministic systems are relatively easy to understand and analyse, once the transitions are fully known.

注意到每一个状态都仅仅依赖于前一个状态，所以如果灯是绿色的，则下一个肯定是黄色的-也就是这个系统是确定性的。一旦转移的关系都清楚之后，确定性的系统相对来说易于理解和分析。

2.2 Non-deterministic patterns（非确定的模式）

To make the weather example a little more realistic, introduce a third state - cloudy. Unlike the traffic light example, we cannot expect these three weather states to follow each other deterministically, but we might still hope to model the system that generates a weather pattern.

为了让天气的例子更为实际，引入了第三个状态-多云。不像交通灯的例子，我们不能够期望这三个天气的状态确定性的进行转换，但我们仍然可以希望建立一个系统来产生天气的模式。

One way to do this is to assume that the state of the model depends only upon the previous states of the model. This is called the Markov assumption and simplifies problems greatly. Obviously, this may be a gross simplification and much important information may be lost because of it.

一种方法是假设模型的状态仅仅依赖于这个模型上一次的状态。这被称作马尔科夫假设并能够大大简化问题。显然，这是一种粗略的简化，并因此可能会丢失大量的信息。

When considering the weather, the Markov assumption presumes that today's weather can always be predicted solely given knowledge of the weather of the past few days - factors such as wind, air pressure etc. are not considered. In this example, and many others, such assumptions are obviously unrealistic. Nevertheless, since such simplified systems can be subjected to analysis, we often accept the assumption in the knowledge that it may generate information that is not fully accurate.

当考虑天气的时候，仅仅给出了前几天的天气情况的条件下（其他影响的因素如：风，气压等都没有考虑），马尔科夫假设假定今天的天气总是能够被预测出来。在这个例子中，以及其他很多的例子中，如此的假设非常的不实际。然而，因为如此简化后的系统能够被拿来分析，我们常常接受这样一个对于知识的假设，尽管它可能会产生一些不完全正确的信息。

2.2 Non-deterministic patterns（非确定的模式）

To make the weather example a little more realistic, introduce a third state - cloudy. Unlike the traffic light example, we cannot expect these three weather states to follow each other deterministically, but we might still hope to model the system that generates a weather pattern.

为了让天气的例子更为实际，引入了第三个状态-多云。不像交通灯的例子，我们不能够期望这三个天气的状态确定性的进行转移，但我们仍然可以希望建立一个系统来产生天气的模式。

One way to do this is to assume that the state of the model depends only upon the previous states of the model. This is called the Markov assumption and simplifies problems greatly. Obviously, this may be a gross simplification and much important information may be lost because of it.

一种方法是假设模型的状态仅仅依赖于这个模型上一次的状态。这被称作马尔科夫假设并能够大大简化问题。显然，这是一种粗略的简化，并因此可能会丢失大量的信息。

When considering the weather, the Markov assumption presumes that today's weather can always be predicted solely given knowledge of the weather of the past few days - factors such as wind, air pressure etc. are not considered. In this example, and many others, such assumptions are obviously unrealistic. Nevertheless, since such simplified systems can be subjected to analysis, we often accept the assumption in the knowledge that it may generate information that is not fully accurate.

当考虑天气的时候，仅仅给出了前几天的天气情况的条件下（其他影响的因素如：风，气压等都没有考虑），马尔科夫假设假定今天的天气总是能够被预测出来。在这个例子中，以及其他很多的例子中，如此的假设非常的不实际。然而，因为如此简化后的系统能够被拿来分析，我们常常接受这样一个对于知识的假设，尽管它可能会产生一些不完全正确的信息。

A Markov process is a process which moves from state to state depending (only) on the previous n states. The process is called an order n model where n is the number of states affecting the choice of next state. The simplest Markov process is a first order process, where the choice of state is made purely on the basis of the previous state. Notice this is not the same as a deterministic system, since we expect the choice to be made probabilistically, not deterministically.

一个过程从一个状态转移到另一个状态仅仅依赖于前n个状态被称作马尔科夫过程。这个过程被称作n阶（n order）模型，n表示能影响下一个状态选择的以前状态的数量。最简单的马尔科夫过程是一阶过程，也就是状态的选择仅仅基于上一个状态。注意这与确定性系统不同，因为我们期望做出的选择是或然的而不是必然的。

The figure below shows all possible first order transitions between the states of the weather example.

这幅图显示了天气的例子中的状态的所有可能的一阶转移。

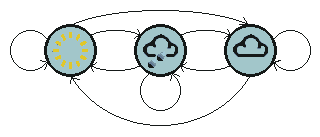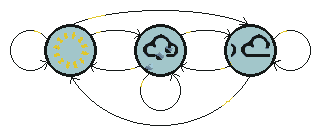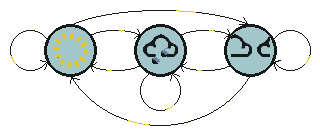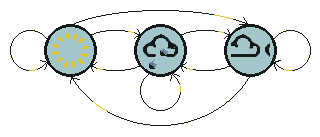
Notice that for a first order process with M states, there are M² transitions between states since it is possible for any one state to follow another. Associated with each transition is a probability called the state transition probability - this is the probability of moving from one state to another. These M² probabilities may be collected together in an obvious way into a state transition matrix. Notice that these probabilities do not vary in time - this is an important (if often unrealistic) assumption.

注意到对于一个一阶的马尔科夫过程有M个状态，则状态间会有M^2个转移，因为对于任何一个状态都可能转移到任意一个其他状态。每个转移都关联这一个概率称作状态转移概率-它是从一个状态转移到另一个状态的概率。这些M ^2个概率可能可以被收集在一起用一种明确的方法放在一个状态转移矩阵中。注意到这些概率不会随时间改变——这是一个非常重要的假设（尽管实际情况常常不是这样）。

The state transition matrix below shows possible transition probabilities for the weather example;

下面的这个状态转移矩阵显示了在天气的例子中可能的转移概率；

- that is, if it was sunny yesterday, there is a probability of 0.5 that it will be sunny today, and 0.25 that it will be cloudy or rainy. Notice that (because the numbers are probabilities) the sum of the entries for each column is 1.

——也就是，如果昨天是晴天，那么有0.5的概率今天也是晴天，各有0.25的概率会是多云或下雨。注意到表中每列之和都是1（因为这些数字都是概率<因为总会有一个状态会转移到这个状态>）。

To initialize such a system, we need to state what the weather was (or probably was) on the day after creation; we define this in a vector of initial probabilities, called the vector.

为了初始化这样一个系统，我们需要在创建后的这天声明天气是怎样（或可能是怎样）；我们把这定义为一个初始化的概率向量，称作向量 。

- that is, we know it was sunny on day 1.

- 如上，这就是说我们知道第一天是晴天。

We have now defined a first order Markov process consisting of :

我们现在已经定义了一个一阶的马尔科过程由以下部分组成：

• states : Three states - sunny, cloudy, rainy.
  状态：3个状态——晴，多云，雨。
• vector : Defining the probability of the system being in each of the states at time 0.
  向量 ：定义了系统在0时刻停留那一个状态的概率。
• state transition matrix : The probability of the weather given the previous day's weather.
  状态转移矩阵：根据前一天的天气来判断今天天气是何种状态的概率。

Any system that can be described in this manner is a Markov process.
任何可以被描述成为这样一种形式的系统就是马尔科夫过程。

2.3 Summary

We are trying to recognize patterns in time, and in order to do so we attempt to model the process that could have generated the pattern. We use discrete time steps, discrete states, and we may make the Markov assumption. Having made these assumptions, the system producing the patterns can be described as a Markov process consisting of a vector and a state transition matrix. An important point about the assumption is that the state transition probabilites do not vary in time - the matrix is fixed throughout the life of the system.

我们为了识别出关于时间的模式，所以我们试图对能够产生模式的过程进行建模。我们使用离散的时间步，离散的状态，并且我们可以使用马尔科假设。做了这么多的假设之后，产生模式的系统可以被描述成一个由一个π向量和一个状态转移概率矩阵的马尔科夫过程。关于这个假设非常重要的一点是状态转移概率并不随时间而改变——这个矩阵在这个系统整个的生命中是不会发生改变的。