一枚菜鸟的leetcode刷题笔记 - Day10

124 - 二叉树中的最大路径和

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。该路径 至少包含一个 节点，且不一定经过根节点。路径和 是路径中各节点值的总和。给你一个二叉树的根节点 root ，返回其 最大路径和。

示例一：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZkqxOCI3-1611197311847)(media/16081082147898/exx1.jpg)]
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.maxSum = float('-inf')  #maxSum如果不设置为类的属性，会报错
    
    def maxPathSum(self, root: TreeNode) -> int:
        def maxUpPath(node):
            if not node:
                return 0    #base情况，叶子节点的左右子节点(None)被设置为0
            leftSum = max(maxUpPath(node.left), 0)
            rightSum = max(maxUpPath(node.right), 0)
            if leftSum + rightSum + node.val > self.maxSum:
                self.maxSum = leftSum + rightSum + node.val
            return max(leftSum, rightSum) + node.val

        maxUpPath(root)
        return self.maxSum

这道题目完全参考了官方解答，我自己想根本不可能想出来的。

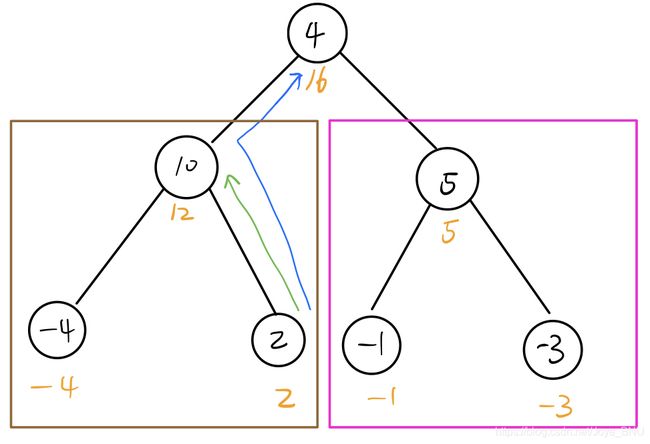
对于树的每一个节点，都计算一个以该节点为尾节点的最大上升路径和 maxUpPath(node)，该最大上升路径和是当前节点与其左右子树中的较大者求和的来，如图中的黄色数字，它有如下几种情况：

1. 若该节点的左右子树的最大上升路径和均为负值，那么该节点的最大上升路径和为其本身的值，如粉红色框起来的部分；
2. 若该节点的左右子树的最大上升路径和至少有一个是正值，那么该节点的最大上升路径和为其本身的值 + 左右子树中最大上升路径和较大者，如棕色框起来的部分；
   公式表示为：maxUpPath(node) = max(max(maxUpPath(node.left), 0), max(maxUpPath(node.right), 0)) + node.val. 遍历二叉树，得到所有节点的最大上升路径和。

但是此时还没有得到最大路径和，因为路径可能包含下降段，这就需要记录以当前节点为中心节点的最大路径和。并且维护另一变量maxSum，用来记录目前为止遇到的以不同节点为中心节点的最大路径和。即记录最大的 max(maxUpPath(node.left), 0) + max(maxUpPath(node.right), 0) + node.val. 最后当遍历完二叉树，maxSum就是我们要找的路径和。

• 解题思路类似于数组的最大子数组和，当时用了动态规划：dp[i] 代表以 nums[i] 为结尾的子数组的最大和。转移方程：dp[i] = max(dp[i-1], 0) + nums[i]

• 为什么不能直接维护以当前节点为中心顶点的最大路径和呢？
  很简单，因为此种情况没办法写出转移方程，该节点的最大路径和倒是写出来了，那么上一级节点呢，没有联系性。

121 - 买卖股票最佳时机

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。
注意：你不能在买入股票前卖出股票。

示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        ret = 0
        for i in range(n-1):
            for j in range(i+1, n):
                if prices[j] - prices[i] > ret:
                    ret = prices[j] - prices[i]
        return ret

超时了。两重循环的想法本质上是以prices数组中的每一个值为起点，然后在该值后面找使利润最大的值。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        minVal = prices[0]
        ans = 0
        for i in range(1,n):
            if prices[i] < minVal:
            #只有小于min的值才可能导致更大的利润出现
                minVal = prices[i]
            if prices[i] - minVal > ans:
                ans = prices[i] - minVal
        return ans

但其实不是每一个值都有必要作为起点，精简循环的方法是使用变量min记录下当前储存的最小值，存储min的目的是为寻找下一个可能出现的最大回报，而不是说当前的min就一定是最大回报的起始值。例如 prices = [7,2,8,1,6,4,3]，最大 return 为 8-2=6，但是最终 min 值为 1. 若后续prices[i]与当前最小值的差值大于当前ans，则更新ans.

本解法通过给定min和ans的初始值，并不断更新min和ans减少了一重循环。

122 - 买卖股票的最佳时机 II

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例一：
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        ans = 0
        n = len(prices)
        for i in range(1, n):
            ret = prices[i] - prices[i-1]
            if ret > 0:
                ans += ret
        return ans

完全参考了买卖股票的最佳时机 II （贪心，清晰图解）