分治法原理和其应用（循环赛问题和最近点对问题）

Divide and Conquer

分而治之

前言：
即将迎来紧张刺激的期末考试，灵机一动，想出更博以促学习，妙哉。

问题能用分治法求解的三要素

1.分解
原问题能够按一定方法分解成若干规模较小，相对独立，且与原问题类型相同的子问题。
2.求解
子问题足够小时可以求解
3.合并
能够将子问题的解组合成原问题的解

---

分治法的应用

目录：

• 1.循环赛问题
• 2.最近点对问题

1.循环赛问题

问题描述：
有$n(n=2^k$)个队伍参加循环赛，要求设计满足以下要求的比赛日程表：
(1)每个队伍每天要比赛一场
(2)每个队伍要与其他$n-1$个队伍比赛一次
(3)比赛进行$n-1$天

问题分析：
每天进行$n/2$场比赛

解决方案：
以8个队伍为例

日程表设计


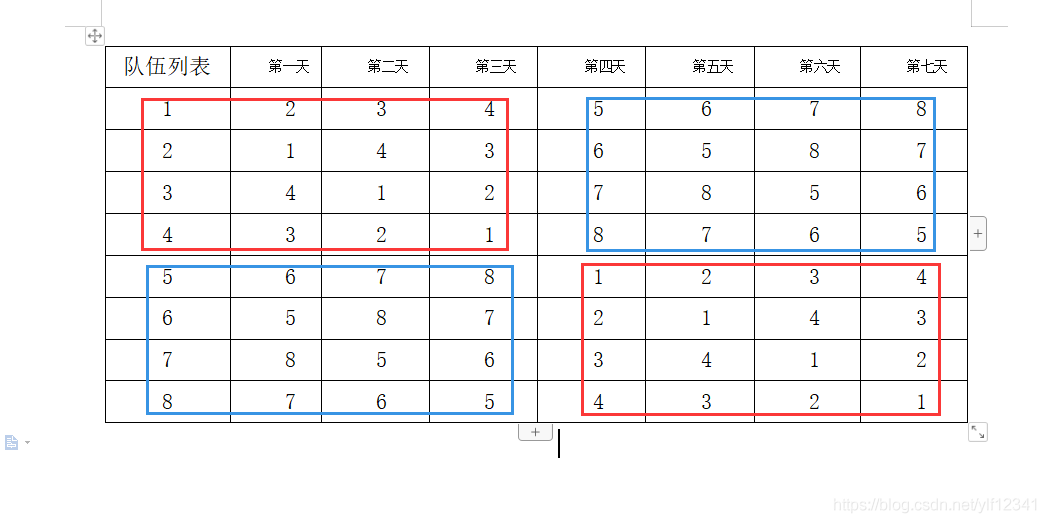
根据已经得到的8个队伍的日程表，可以发现解决问题的一些特性
1.可以把整个比赛赛程分成两半
一共7天的比赛日程分成前3天和后4天
2.把所有队伍分成两个赛区
规定比赛的前半程，为同属赛区互殴 （同一个赛区除了自己打3场）
比赛的后半程为不同赛区的队伍互殴 （不同赛区打满4场）

以上图左上角矩阵为例，一共四个队伍（1,2,3,4）,比赛三天。

容易发现
满足题目要求的矩阵生成策略是：
每一行，每一列，都没有一个相同的数字

那么在左上角矩阵的基础上，给每个元素加4，可以得到右上角的矩阵和左下角的矩阵
1.右上角的矩阵自身满足题目要求
2.右上角的矩阵中不会出现左上角矩阵出现的数字
这样就可以判断出上方生成的矩阵是正确的

思路：
解决上述问题，8个队伍的比赛可以由4个队伍比赛的日程决定

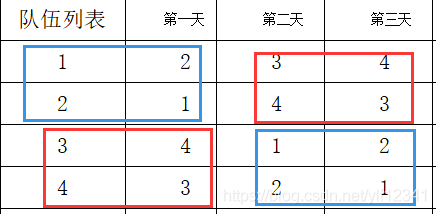
那么4个队伍的比赛日程可以由2个队伍比赛决定

这时候我们可以脱离这个题目的限制了，我们要知道的是，要解决题目
只要用算法生成一个每一行每一列都不同的矩阵就行了
这是一种解决问题的办法
如果硬是要把算法和题目联系在一起，就会很难受，因为矩阵的第一列在题目中的意义是队伍列表，和其他元素代表的意义不同
网上有人把第一列硬是看成了第0天自己和自己打（自己预热）
但考虑到整个赛程安排依赖于左上角的矩阵生成

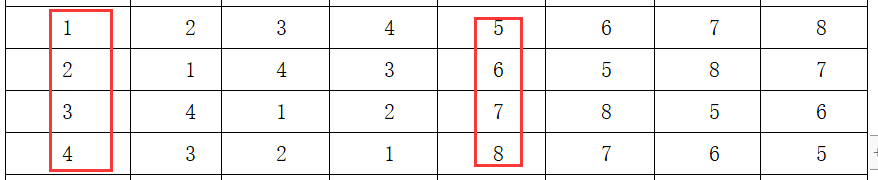
按照他的方法 左边的1234说的过去，但是右边的5678难道也是自己打自己吗？
但这个同学也是在努力的说服自己，让自己感觉舒适，说明他懂得自洽的重要性。

实际上，应该先从比赛入手，找到了一种矩阵生成策略，可以满足题目的要求
那么就把注意力集中在矩阵生成的过程中，跳出这个比赛的限制
我们只要知道，我们生成了这个矩阵，满足题目要求就行了
而这个矩阵生成的要求就是，每一行每一列都不同

反过来
矩阵生成的过程中，整个矩阵的生成依赖于左上角矩阵，而左上角矩阵生成又可以满足前半赛程，第一赛区的比赛要求

那么我们生成左上角矩阵，前半赛程，第一赛区的比赛安排符合要求
生成整个矩阵，所有比赛的比赛安排符合要求

矩阵生成运用了分治法的思想，那么整个题目也用到了分治法的思想

矩阵生成后，我们只要能理解矩阵的第一列是队伍列表的意思，2到n列是每一天的意思就行了

算法：
初始化一个数组a[n-1][n-1]
输入:队伍数目n
void round-robin(int n，int [][] a)
1.$n=0$的时候
$a[0][0]=1;$

2.$n>0$的时候
把问题一分为二
递归地把左上角的矩阵生成好
然后根据左上角矩阵，让右上角矩阵对应元素+n/2
再把左下角元素和右上角元素对应起来
右下角元素和左上角元素对应起来

整个问题的解决过程如下

---

3.最近点对问题

知识点：鸽舍定理
原理（一）：把多于n个元素，分配到n个集合，那么一定至少有一个集合中，至少有两个元素。
原理（二）：把多于m*n个物体放到n个抽屉中，那么一定有一个抽屉里有m+1或者m+1个以上的物体。

感觉像是废话，哈哈哈哈

问题描述：
n个点在公共空间中，求出所有点对中，欧几里得距离最小的点。
翻译：n个点找到距离最近的两个点。

解决方案：
运用分治法的思想，把所有点分成左右两堆
考虑三种情况：
（1）符合要求的点都在左边的堆
（2）符合要求的点都在右边的堆
（3）符合要求的点一个在左边，一个在右边

1.按什么方法把所有点分成两个部分？
获取所有点的横坐标X，进行一次快排，把按照X排序过的点存入数组
取数组的中间点的横坐标m,以$X=m$为分界线把点集分成两部分

2.这时候把一个大问题分成了两个子问题，两个子问题求解得到两组点，两个最小值。
取二者之中的更小值为最小值a。

3.现在要分析第三种情况一个在左边一个在右边
要想这样的情况成立，至少要满足两个点之间横坐标之差不能大于a
考虑左边点接近边界线的极限情况，右边点能出现的最远边界是$X=m+a$
相反情况下，左边点能出现的最远边界是$X=m-a$
故，要想在第三种情况下取得极小值 首先要满足点在红线范围内。

4.现在来获取这些落在范围X=m-a 到 X=m+a内的点
遍历之前的数组，得到符合条件的点集set[],左右点都放在其中

5.遍历所有的左边点集，与右边的点比较，为了减少时间复杂度，希望比较的次数越少越好。
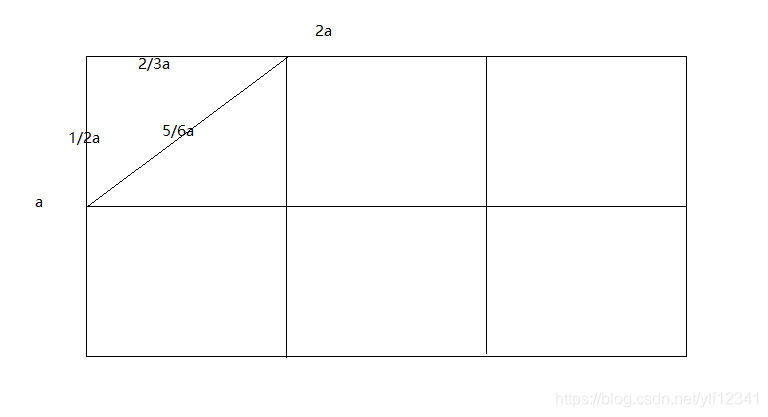
取左边点（x1,y1）,划定右边点可能存在的空间
只能是X=m 到 X=m+a Y=y1-a 到 Y=y1+a的矩形空间中
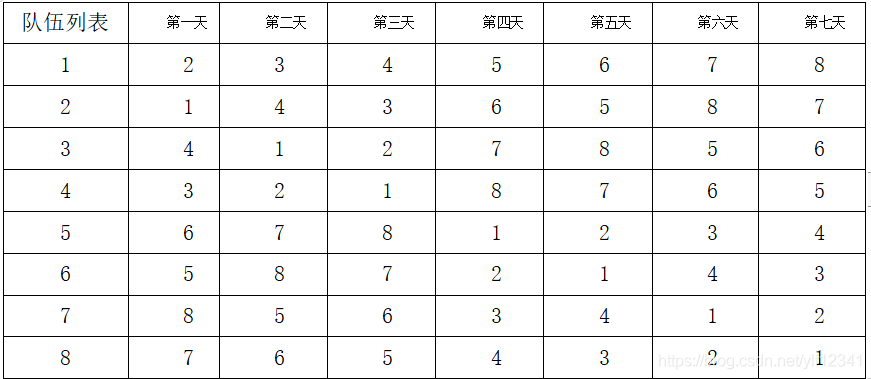
X的限制不用说，Y的限制是只考虑纵坐标之差要小于a,即下图中的2a*a的矩形区域

前面的鸽舍定理干嘛用的，就是这个时候用的
考虑到这个矩形区域的点有个前置条件，两点之间的距离要小于等于a,因为a是左右两堆中点对距离的最小值。
那么问题就是：在这个矩形区域中，任意两点距离大于等于a的情况下，最多有几个点？
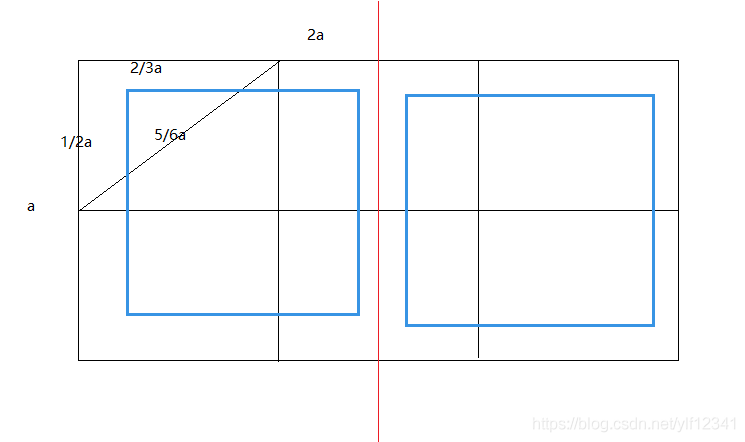
考虑下图：
由鸽舍定理知：
假设我们有6个以上的点，分配到这6个格子中，那么至少一个格子中，会出现两个以上的点。
但是在一个格子中，最大距离小于a,不满足前提条件，也就是说一个格子里最多一个点。
那么我们得到结论：
选择左侧一个点，在满足条件的区域内，右侧最多有6个点满足情况，可以考虑离左边这个点（Y值）最近的6个右边的点。
（据可靠的小道称，已经证明只有至多四个点满足情况）

6.接下来就是取得这些点，进行比较，更新最小值
把之前符合条件的点集set[] 按照Y值，进行一次快排。
这样可以比较快的得到目标点最近的点
具体怎么能刚好只比较6个点还比较难以操作
在不需要做多余判断的情况下，能想出来的办法就是往上找4个点，往下找4个点
因为上方下方空间最多包含4个格子

7.每个子问题的都与原问题类型相同，应用分治法可以解决上述问题。

---

原来计划昨天晚上就完成的，没想到这个编辑软件这么原始，都没有改变字体颜色的欲望，打字像是在敲代码，一直到现在将近12点，我竟然克服了打一把人机的欲望，正是难以想象。

代码就不贴了，给个解题思路。

“为什么是晚霞？”
“晚霞过后有星星，有月亮，朝霞过后…”
“就只剩光天化日下的现实…”