9.人工智能原理-深度学习：神奇的DeepLearning
目录
一、深度学习
二、Tensorflow
sigmoid函数的梯度消失：
relu激活函数
三、编程实验
四、总结
五、往期内容
一、深度学习
正如我们在第六节课中说的那样，深度学习就是不断的增加一个神经网络的隐藏层神经元，让输入的数据被这些神经元不断的抽象和理解，最后得到一个具有泛化能力的预测网络模型。而我们一般把隐藏层超过三层的网络也就称之为深度神经网络。
如此说来，深度学习这个听起来相当高端大气上档次，尤其是近些年来被媒体包装的十分具有神秘感的名字，瞬间你就觉得没有那么的道貌岸然。至于网络中每个节点到底在理解什么，很难用精确的数学手段去分析，我们唯一能做的事情就是收集数据，送入数据，进行训练，然后期待结果。当然，也不是说我们对一个深度神经网络完全不可把控，起码我们能在比如学习率、激活函数、神经元的层数和数量等等方面调节神经网络的大致工作行为，俗称调参。
二、Tensorflow
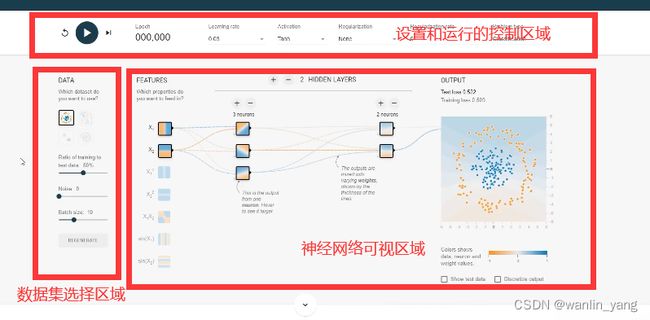
我们以著名的Tensorflow游乐场为例:
1.我们先选择第三个数据集，调参模拟训练一下：
分类的方式我们也说过，那就是让预测函数曲面的0.5等高线把它们分割开来。我们知道对于这种线性可分的问题，使用单个的神经元就可以完成分类，所以我们点击隐藏层的设置区域的减号，把隐藏层减少到0层，也就是说只保留一个输出层的神经元。好的，我们再设置一下神经元的激活函数，这里它默认使用的是双曲正切tanh函数，这个激活函数目前为止我们还没有接触道，那么我们还是选择熟悉的老伙计sigmoid函数,学习率设置为0.03，然后点击运行按钮运行一下，果然很轻松的就让输出预测曲面的0.5等高线完美的分割了两类豆豆。
训练结果：
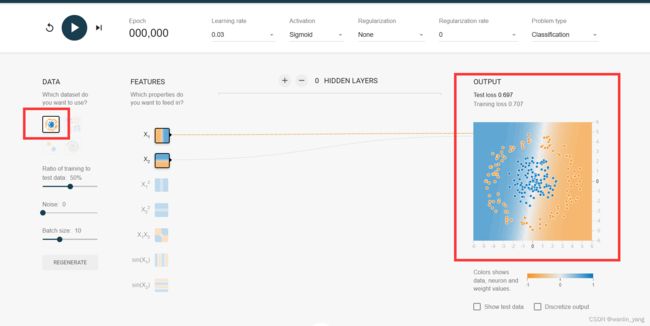
2.我们再试试第一个数据集：
我们思考，这个需要几个神经元来分类呢？
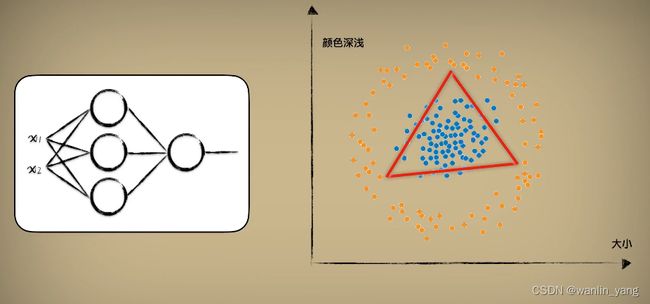
我们定性分析一下，还是看图说话，一个神经元是一条直线，三个神经元形成三条直线刚好形成闭合的形状。
把这三个神经元的计算结果再通过一个输出层的神经元进行汇合，通过sigmoid的激活函数修饰一下之后就可以了。如此也就可以解决这种圈圈分布数据的分类问题，圈内是一类，圈外是另一类。我们点击隐藏层设置区域的加号，把隐藏层增加到1层，再点击这一层的设置区域上的加号，把这一层的神经元数量增加到3个，如此就得到了一个有3个神经元的1层隐藏层，学习率还是0.03，不必修改，运行一下，最后输出的预测曲面的0.5等高线也完美的分割出了这两枚豆豆。
3.再来看看第二个数据集：
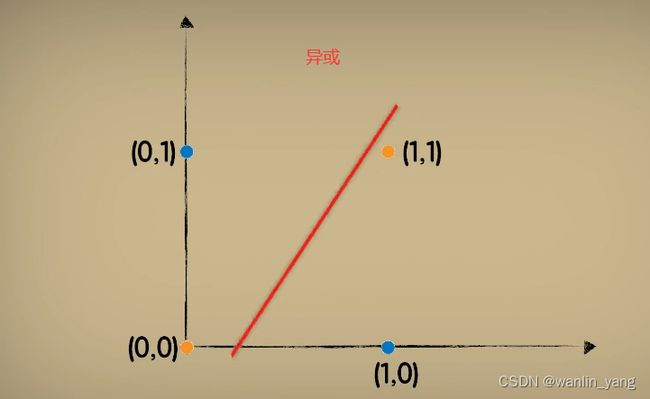
异或：这实际上就是在感知器最初发展阶段困扰研究人员很多年的一个问题。当时为了证明感知器模型并没有太大的卵用，于是人们提出了一种在计算机领域非常常见的问题，异或。
想要分割出这种分布数据的类型，单个神经元的感知器是无法做到这一点的，如此简单的问题都无法分类，所以证明感知器并没有什么卵用。但现在我们知道，实际使用具有包含三个神经元的隐藏层的神经网络就可以顺利的做出分类。
4.我们再来看最后一个蚊香一样的螺旋性数据集：
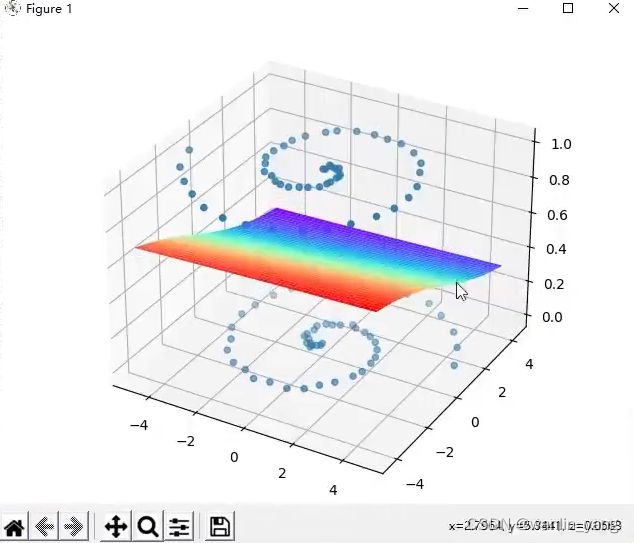
很明显只有一层包含3个神经元的隐藏层的神经网络在这种复杂的数据集上将表现得十分疲软，那我们就用更深、神经元数量也更多的网络来尝试一下。
一般的深度网络只超过三层，把隐藏层的数量增加到3层，每个隐藏层用4个神经元运行一下。
预测结果随着训练动也不动，这是因为我们的老伙计“sigmoid”的激活函数的问题。
sigmoid函数的梯度消失：
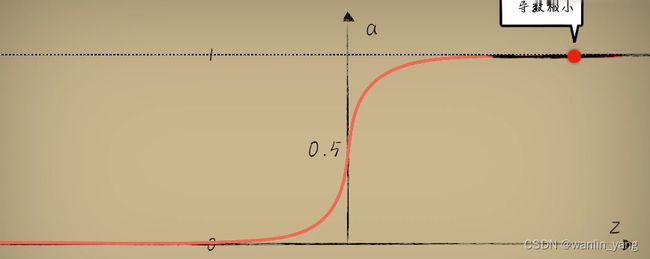
我们之前说过，之所以选择sigmoid的函数作为激活函数，那是因为相比于阶跃函数，sigmoid函数处处可到，而且导数处处不为零，这样在反向传播的时候，我们知道使用梯度下降算法计算函数的导数，然后利用这个导数去修正参数。但是我们并没有说sigmoid其实有一个很严重的问题，在sigmoid的中心位置附近，这没有啥问题，但如果一旦进入了sigmoid函数远离中心点的位置，比如这里虽然仍旧可导，导数仍旧不为零，但是导数却极其的小，这样梯度下降就很难进行。距离中心越远的位置，这个导数越小，也就是说所谓的梯度消失的问题，越深的神经网络就越容易出现这种梯度消失的问题，所以这个网络变的很难训练。
relu激活函数
所以目前人们普遍不再使用sigmoid结果函数，而经常使用一种叫做relu的激活函数，这是一个分段函数：
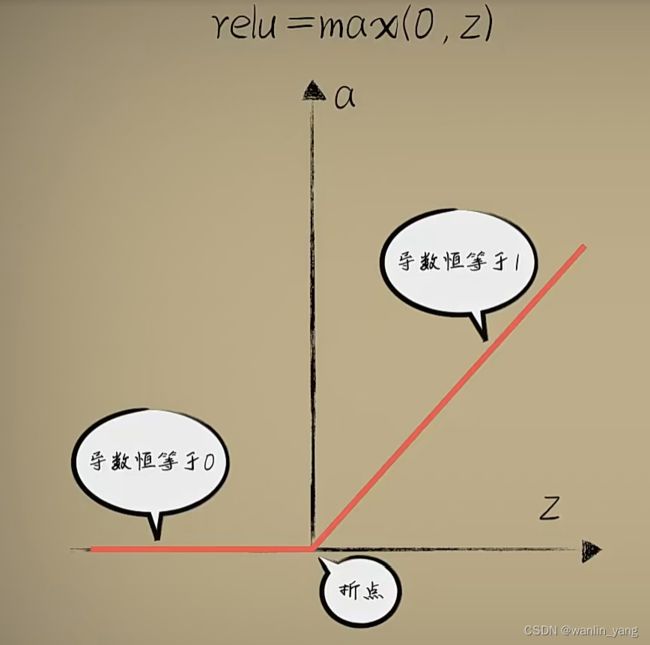在Z=0的时候出现了折点，从数学上来看，这个折点确实不可导数，但一般很难恰好遇到这个点，真要是遇到的，那就特殊处理一下，比如认为这一点的导数是0或者1，或者一个很小的值，比如0.01。
如果陷入了Z<0的部分，很有可能导致这个神经元死亡，也就是所谓的Dead Relu Problem。
死亡Relu问题因为根据反向传播中的链式求导法则，如果激活函数的导数是0，那么就锁定了这个神经元上的参数梯度为0，权重无法更新。
所以人们又提出了一种改进版的Relu函数(leaky-relu):
在Z小于零的时候，输出不再是零，而是一个缓缓倾斜的直线，如此就可以避免死亡Relu问题。
不过梯度消失不止与激活函数有关，还有其他因素有关，目前也有很多相关的研究，但按照经验使用relu激活函数都会有不错的效果。所以现在最为流行的激活函数还是relu。
我们就把激活函数改为relu，再练习一下：
实际上对于我们刚才研究的圈圈分布的数据，你会发现如果使用relu激活函数会比sigmoid函数，收敛的过程会更加的迅速。实际上对于隐藏层的神经元，如果没有其他想法或者特殊的需求，relu应该作为激活函数的第一选择。当然在最后的输出层，因为sigmoid的上下线刚好在0到1之间，很适合做分类，所以输出层的激活函数还是选择sigmoid。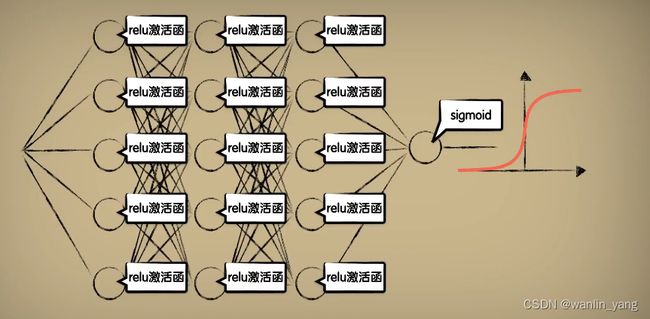
我们把每层的神经元增加到8个，看看效果如何：
结果表明，神经元越多，效果越好！
三、编程实验
本节课用Karas搭建一个深度神经网络，拟合一下这个长得像蚊香一样的螺旋性数据集。
1.豆豆数据集dataset.py
import numpy as np
import random
def get_beans(counts):
posX,posY = genSpiral(int(counts/2),0,1)
negX,negY = genSpiral(int(counts/2),np.pi,0)
X = np.vstack((posX,negX))
Y = np.hstack((posY,negY))
return X,Y
def genSpiral(counts,deltaT, label):
X = np.zeros((counts,2))
Y = np.zeros(counts)
for i in range(counts):
r = i / counts * 5
t = 1.75 * i / counts * 2 * np.pi + deltaT;
x1 = r * np.sin(t) + random.uniform(-0.1,0.1)
x2 = r * np.cos(t) + random.uniform(-0.1,0.1)
X[i] = np.array([x1,x2])
Y[i] = label
return X,Y
def dist(a, b):
dx = a['x'] - b['x'];
dy = a['y']- b['y'];
return np.sqrt(dx * dx + dy * dy);
def getCircleLabel(p, center):
radius = 1;
if dist(p, center) < (radius * 0.5):
return 1
else:
return 0
def randUniform(a=-1, b=1):
return np.random.rand() * (b - a) + a;
def classifyCircleData(numSamples=100, noise=0):
points = [];
Y = []
X = []
radius = 1;
num = int(numSamples/2)
for i in range(num):
r = randUniform(0, radius * 0.5);
angle = randUniform(0, 2 * np.pi);
x = r * np.sin(angle);
y = r * np.cos(angle);
noiseX = randUniform(-radius, radius) * noise;
noiseY = randUniform(-radius, radius) * noise;
label = getCircleLabel({'x': x + noiseX, 'y': y + noiseY}, {'x': 0, 'y': 0});
X.append([x+1,y+1])
Y.append(label)
for i in range(num):
r = randUniform(radius * 0.7, radius);
angle = randUniform(0, 2 * np.pi);
x = r * np.sin(angle);
y = r * np.cos(angle);
noiseX = randUniform(-radius, radius) * noise;
noiseY = randUniform(-radius, radius) * noise;
label = getCircleLabel({'x': x + noiseX, 'y': y + noiseY}, {'x': 0, 'y': 0});
X.append([x+1,y+1])
Y.append(label)
X = np.array(X)
Y = np.array(Y)
return X,Y豆豆毒性大小分布如下：
2.绘图封装工具：plot_utils.py
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from keras.models import Sequential#导入keras
def show_scatter_curve(X,Y,pres):
plt.scatter(X, Y)
plt.plot(X, pres)
plt.show()
def show_scatter(X,Y):
if X.ndim>1:
show_3d_scatter(X,Y)
else:
plt.scatter(X, Y)
plt.show()
def show_3d_scatter(X,Y):
x = X[:,0]
z = X[:,1]
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x, z, Y)
plt.show()
def show_surface(x,z,forward_propgation):
x = np.arange(np.min(x),np.max(x),0.1)
z = np.arange(np.min(z),np.max(z),0.1)
x,z = np.meshgrid(x,z)
y = forward_propgation(X)
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(x, z, y, cmap='rainbow')
plt.show()
def show_scatter_surface(X,Y,forward_propgation):
if type(forward_propgation) == Sequential:
show_scatter_surface_with_model(X,Y,forward_propgation)
return
x = X[:,0]
z = X[:,1]
y = Y
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x, z, y)
x = np.arange(np.min(x),np.max(x),0.1)
z = np.arange(np.min(z),np.max(z),0.1)
x,z = np.meshgrid(x,z)
X = np.column_stack((x[0],z[0]))
for j in range(z.shape[0]):
if j == 0:
continue
X = np.vstack((X,np.column_stack((x[0],z[j]))))
print(X.shape)
r = forward_propgation(X)
y = r[0]
if type(r) == np.ndarray:
y = r
y = np.array([y])
y = y.reshape(x.shape[0],z.shape[1])
ax.plot_surface(x, z, y, cmap='rainbow')
plt.show()
def show_scatter_surface_with_model(X,Y,model):
#model.predict(X)
x = X[:,0]
z = X[:,1]
y = Y
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x, z, y)
x = np.arange(np.min(x),np.max(x),0.1)
z = np.arange(np.min(z),np.max(z),0.1)
x,z = np.meshgrid(x,z)
X = np.column_stack((x[0],z[0]))
for j in range(z.shape[0]):
if j == 0:
continue
X = np.vstack((X,np.column_stack((x[0],z[j]))))
print(X.shape)
y = model.predict(X)
# return
# y = model.predcit(X)
y = np.array([y])
y = y.reshape(x.shape[0],z.shape[1])
ax.plot_surface(x, z, y, cmap='rainbow')
plt.show()
def pre(X,Y,model):
model.predict(X)3. 梯度下降代码（套用上节课代码）：beans_predict0.py
import dataset
import plot_utils
from keras.models import Sequential #堆叠神经网络序列的载体
from keras.layers import Dense #全连接层，一层神经网络
from keras.optimizers import SGD #引入keras.optimizers调整学习率
#获取豆豆数据
m = 100
X, Y = dataset.get_beans(m)
plot_utils.show_scatter(X, Y)
#创建堆叠神经网络序列的载体Sequential
model = Sequential()
#创建全连接层
# 当前层神经元的数量为2，激活函数类型：sigmoid，输入数据特征维度：2
model.add(Dense(units=2, activation='sigmoid', input_dim=2))
model.add(Dense(units=1, activation='sigmoid'))#输出层
#配置模型
model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.05), metrics=['accuracy'])
# loss（损失函数、代价函数）：mean_squared_error均方误差；
# # optimizer（优化器）：sgd（随机梯度下降算法）；
# metrics（评估标准）：accuracy（准确度）；
#训练数据fit
model.fit(X, Y, epochs=5000, batch_size=10)
# epochs：回合数（全部样本完成一次训练）、batch_size：批数量（一次训练使用多少个样本）
#预测数据predict
pres = model.predict(X)
plot_utils.show_scatter_surface(X, Y, model)
#得到模型的各个参数数据
print(model.get_weights())可以看出，训练结果不太行
看看最后得出的参数：
4.梯度下降代码：beans_predict.py
import dataset
import plot_utils
from keras.models import Sequential #堆叠神经网络序列的载体
from keras.layers import Dense #全连接层，一层神经网络
from keras.optimizers import SGD #引入keras.optimizers调整学习率
#获取豆豆数据
m = 100
X, Y = dataset.get_beans(m)
plot_utils.show_scatter(X, Y)
#创建堆叠神经网络序列的载体Sequential
model = Sequential()
#创建全连接层，加入隐藏层
model.add(Dense(units=8, activation='relu', input_dim=2))
# 当前层神经元的数量为8，激活函数类型：relu，输入数据特征维度：1
model.add(Dense(units=8, activation='relu'))
model.add(Dense(units=8, activation='relu'))
model.add(Dense(units=1, activation='sigmoid'))
#配置模型
model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.05), metrics=['accuracy'])
# loss（损失函数、代价函数）：mean_squared_error均方误差；
# # optimizer（优化器）：sgd（随机梯度下降算法）；
# metrics（评估标准）：accuracy（准确度）；
#训练数据fit
model.fit(X, Y, epochs=5000, batch_size=10)
# epochs：回合数（全部样本完成一次训练）、batch_size：批数量（一次训练使用多少个样本）
#预测数据predict
pres = model.predict(X)
plot_utils.show_scatter_surface(X, Y, model)
#得到模型的各个参数数据
print(model.get_weights())训练后图像：
四、总结
深度学习就是收集数据，送入数据，进行训练。我们可以在学习率、激活函数、神经元的层数和数量等等方面调节神经网络的大致工作行为，也就是调参。本节课还介绍了sigmoid函数的梯度消失的问题，从而引进了relu激活函数，但是也有就能出现死亡Relu问题，所以提出了一种改进版的Relu函数(leaky-relu)。本节课编程实验用Karas搭建一个深度神经网络，拟合一下长得像蚊香一样的螺旋性数据集。
五、往期内容
引言：来一场人工智能的奇妙冒险吧~
1.一元一次函数感知器：如何描述直觉
2.方差代价函数：知错
3.梯度下降：能改
4.曲面梯度下降和反向传播：能改
5.激活函数：给机器注入灵魂
6.隐藏层：神经网络为什么working
7.高维空间：机器如何面对越来越复杂的问题
8.初识Keras：轻松完成神经网络模型搭建
9.深度学习：神奇的DeepLearning
10.卷积神经网络：打破图像识别的瓶颈
11. 卷积神经网络：图像识别实战
12.循环：序列依赖问题
13.LSTM网络：自然语言处理实践
14.机器学习：最后一节课也是第一节课
视频链接：
https://pan.baidu.com/s/1fz0CX55bdG7M2t9HQt_wpQ?pwd=m5vz