LeetCode-数据结构(二)
LeetCode-数据结构二
- 第三天-数组
-
- 350-两个数组的交集II
- 121-买卖股票的最佳时机
- 第四天-数组
-
- 566-重塑数组
- 118-杨辉三角
第三天-数组
350-两个数组的交集II
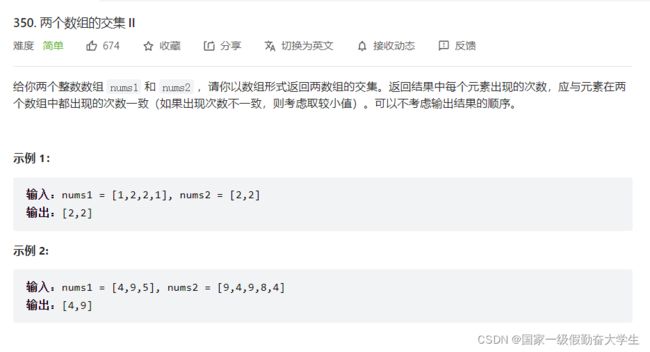
思路1:暴力解法,利用二重循环,定一动一,匹配到相同的则将其存储到vector ans中并将其置为-1
class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
vector<int> ans;
for(auto &it:nums1)
{
for(auto &item:nums2)
{
if(it==item)
{
ans.push_back(it);
item = -1;
break;
}
}
}
return ans;
}
};
思路2:利用排序后两个数组的特点,使用指针分别对两个数组进行查找:
- 当两个指针所指元素值相同时,结果保存,指针右移
- 当指针所指元素值不同时,较小的指针往前移动,直到该指针所指的元素不小于另一个指针所指元素
- 重复12操作,直到有一个指针走完数组中所有的元素,返回答案
class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
sort(nums1.begin(), nums1.end());
sort(nums2.begin(), nums2.end());
int i, j;
i=j=0;
vector<int> ans;
while(i<nums1.size()&&j<nums2.size())
{
if(nums1[i]==nums2[j])
{
ans.push_back(nums1[i]);
i++;
j++;
}
else
{
if(nums1[i]<nums2[j])
{
while(nums1[i]<nums2[j])
{
i++;
if(i>=nums1.size())
return ans;
}
}
else
{
while(nums2[j]<nums1[i])
{
j++;
if(j>=nums2.size())
return ans;
}
}
}
}
return ans;
}
};
思路3:利用unordered_map进行计数
1. 首先初始化存储nums1进入map中
//可以为了优化空间将nums1,nums2进行比较,长度较小的进行初始化存储
2. 对于第二个数组中的元素,count时存在,则说明两个数组中都包含该元素,push_back入ans中
3. 同时计数-1,如果计数为0,说明该元素在nums1中出现次数用完,则erase
class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
unordered_map<int , int> ans;
for(int i:nums1)
{
ans[i]++;
}
vector<int>res;
for(int i:nums2)
{
if(ans.count(i))
{
res.push_back(i);
ans[i]--;
if(ans[i]==0)
{
ans.erase(i);
}
}
}
return res;
}
};
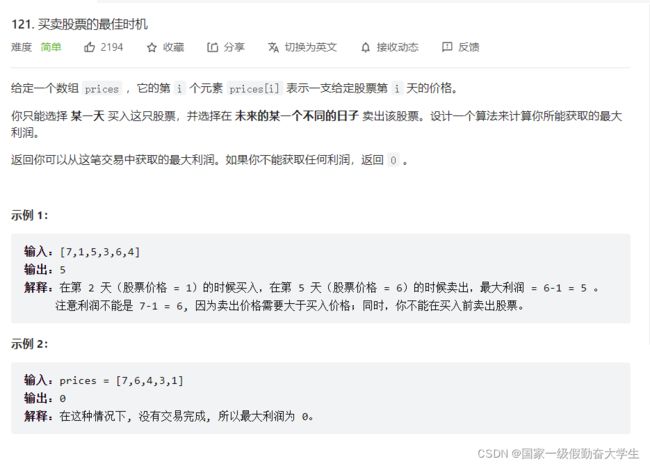
121-买卖股票的最佳时机
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
int n = prices.size();
for(int i=0;i<n-1;i++)
{
for(int j=i;j<n;j++)
{
int temp = prices[j]-prices[i];
ans = max(temp, ans);
}
}
return ans;
}
};
当然暴力是解决不了问题的~
思路二:动态规划
可以用动态规划的思路来解——三个关键思考,子问题划分、初始化和状态转移方程
子问题划分
首先是子问题划分:
第一天我最多能赚多少?
第二天我最多能赚多少?
第三天我最多能赚多少?
……
第i天我最多能赚多少?
最终解决的问题就是这i天中所挣的最大值
子问题细化
第一天我卖股票能挣多少?
第二天我卖股票能挣多少?
第三天我卖股票能挣多少?
……
第四天我卖股票能挣多少?
问题变成如果第i天卖股票,那么我当天能挣多少?
初始化
第一天,由于没有买卖所以,最多赚0,所以初始状态为dp[0] = 0
状态转移方程
如果我第i天一定要卖,那么我在1~i-1天要买进,想要赚的最多,我应该在价格最低的那一天买,所以应该要维护一个最小值,表示卖之前买入的价格,计算完当天的最大利润后,更新答案,更新买入最小值。那么我们就有如下的方程:
dp[i] = max{dp[i-1], prices[i]-m}其中m是维护的买入最小值
m = min{price[i], m}
代码就出来了
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<int>dp(n);
dp[0] = 0;
int m = prices[0];
for(int i=1;i<n;i++)
{
dp[i] = max(dp[i-1], (prices[i]-m));
m = min(m, prices[i]);
}
return dp[n-1];
}
};
第四天-数组
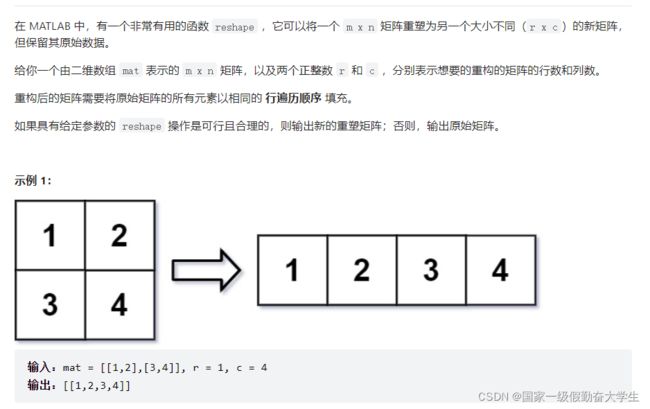
566-重塑数组
1.首先判断其形状是否能够满足reshape的要求,不能则返回mat
2.然后新建一个二维vector数组ans和临时的一维vector数组temp
3.每当填满temp.size()==c时
4.则将其push_back入ans中并进行clear()
5.开始下一行的输入
class Solution {
public:
vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
vector<vector<int>> ans;
if(r*c!=mat.size()*mat[0].size())
return mat;
else
{
vector<int> temp;
for(int i=0;i<mat.size();i++)
{
for(int j=0;j<mat[0].size();j++)
{
temp.push_back(mat[i][j]);
if(temp.size()==c)
{
ans.push_back(temp);
temp.clear();
}
}
}
}
return ans;
}
};
思路2:映射
将二维数组映射到一维数组再映射回二维数组
对于数组a[i][j]来说,假设a的行数为row,列数为col
则其对应的一维坐标为pos = i*col+j
将该一维坐标重新映射回二维坐标,行为n,列为m
x = pos/m
y = pos%m
对于该题我们可以将一维的坐标分别映射到变换前后两个矩阵中,通过上述式子进行reshape的操作
class Solution {
public:
vector<vector<int>> matrixReshape(vector<vector<int>>& nums, int r, int c) {
int m = nums.size();//获取行
int n = nums[0].size();//获取列
if (m * n != r * c) {
return nums;//reshape不匹配则直接返回
}
vector<vector<int>> ans(r, vector<int>(c));//初始化行列
for (int x = 0; x < m * n; ++x) {//一维坐标
ans[x / c][x % c] = nums[x / n][x % n];//变换前后的二维坐标
}
return ans;
}
};
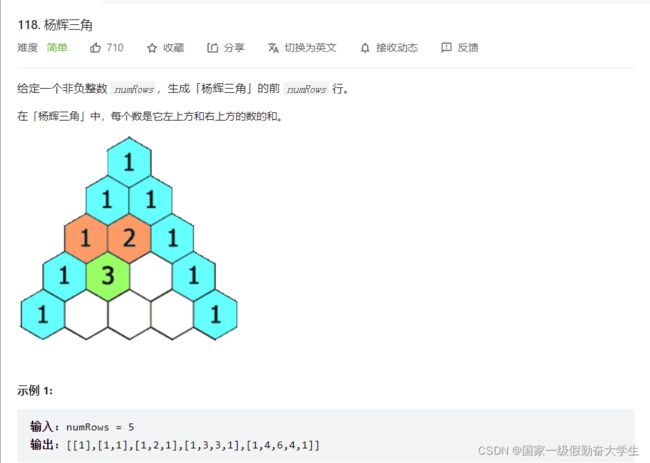
118-杨辉三角
1. 每一行的首尾都是1
2. a[i][j] = a[i-1][j-1] + a[i-1][j]
所以该题的思路就是对于numrow=1或2直接输出即可
当numRow大于2时,先push_back(1),然后利用性质将中间的数字补充,最后push_back(1),重复操作得到答案
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> ans;
vector<int> temp;
temp.push_back(1);
ans.push_back(temp);
if(numRows==1)//特判numRows
return ans;
temp.push_back(1);
ans.push_back(temp);
if(numRows==2)
return ans;
temp.clear();
for(int i=2;i<numRows;i++)
{
temp.push_back(1);//开头插入1
for(int j=1;j<i;j++)
temp.push_back(ans[i-1][j-1]+ans[i-1][j]);//中间用公式补充
temp.push_back(1);//末尾补充1
ans.push_back(temp);
temp.clear();//记得clear
}
return ans;
}
};