2021年 第12届 蓝桥杯 Java B组 省赛真题第一场——杨辉三角形

【问题描述】

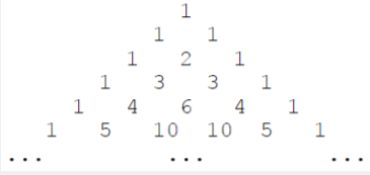
    下面的图形是著名的杨辉三角形：
​
    如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列：

                                        

 

  1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...
​
    给定一个正整数 N，请你输出数列中第一次出现 N 是在第几个数？

【输入格式】输入一个整数 N。

【输出格式】输出一个整数代表答案。

【样例输入】6

【样例输出】13

【评测用例规模与约定】对于 20% 的评测用例，1 ≤ N ≤ 10；对于所有评测用例，1 ≤ N ≤ 1000000000。

阅读完题目你会发现如下规律

 

package test;
import java.util.*;
public class Main {
    public static void main(String[] args) {
    	Scanner sc = new Scanner(System.in);
        long N=sc.nextLong();
        long[] a=new long[44725]; // 通过第二列和第三列关系 可知，在 第 44721行的时候，第三列的值将会超过十亿,所以我们创建 44725长度的数组
        a[0]=1L;
        if(N==1) { //当N==1,直接输出1
        	System.out.println(1);
        	return;
        }
        int count=1; 
        /*
                      * 这里是一个类似于 “递推”的算法，可以在草稿纸进行演算，非常的神奇
         * */
        for(int i=1;i<44725;i++) {
        	for(int j=i;j>=1;j--) {
        		a[j]=a[j]+a[j-1];
        		if(a[j]==N) {  
        					/*找到了N，则输出位置，位置 的计算等于  + 当行的位置数 
        					 * 前面的个数 = (count+1)*count/2  ，当行的个数 = i-j+1
        					 */
        			System.out.println((count+1)*count/2+i-j+1);
        			return;
        		}
        	}
        	count++;
        }
        /*这是未找到的情况，就是说有些数(小于 10 亿的数 )在 44721行之前都还没有出现 ，那么它必然是出现 在 未显示出来在 第二列的位置上
         *	 所以 位置等于 前面出现的个数 + 2
         * */
        System.out.println((N+1)*N/2+2); 
    }
}

如果对你有帮助的话，希望点赞评论+关注哦 ~ . ~  时刻更新blog ，你的支持是我更新的动力 ~