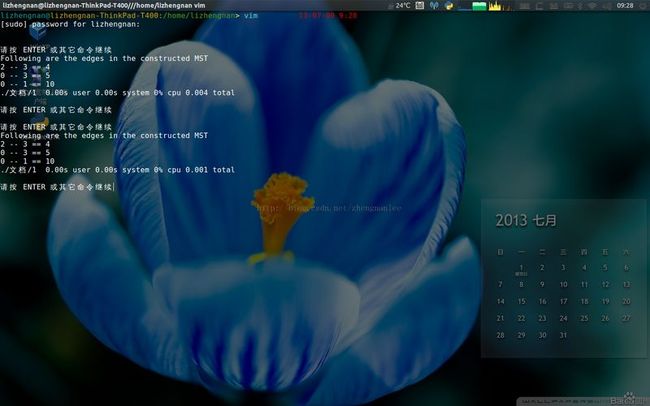
MST(Kruskal’s Minimum Spanning Tree Algorithm)

You may refer to the main idea of MST in graph theory.

http://en.wikipedia.org/wiki/Minimum_spanning_tree

Here is my own interpretation

What is Minimum Spanning Tree?

 

Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.

How many edges does a minimum spanning tree has?

A minimum spanning tree has (V – 1) edges where V is the number of vertices in the given graph.

 

 

Founding MST using Kruskal’s algorithm

1. Sort all the edges in non-decreasing order of their weight.

2. Pick the smallest edge. Check if it forms a cycle with the spanning tree 
formed so far. If cycle is not formed, include this edge. Else, discard it.  

3. Repeat step#2 until there are (V-1) edges in the spanning tree.

 

 

Analise

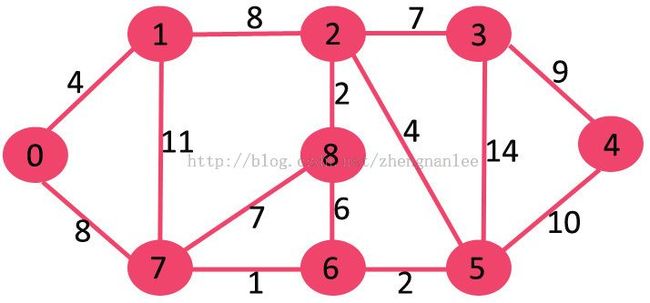
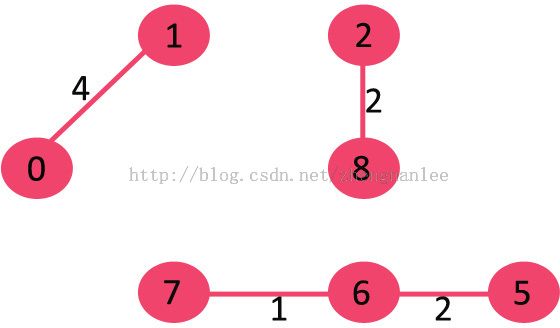
The algorithm is a Greedy Algorithm. The Greedy Choice is to pick the smallest weight edge that does not cause a cycle in the MST constructed so far. Let us understand it with an example: Consider the below input graph.

 

The graph contains 9 vertices and 14 edges. So, the minimum spanning tree formed will be having (9 – 1) = 8 edges.

After sorting:
Weight   Src    Dest
1            7      6
2            8      2
2            6      5
4            0      1
4            2      5
6            8      6
7            2      3
7            7      8
8            0      7
8            1      2
9            3      4
10          5      4
11          1      7
14          3      5

Now pick all edges one by one from sorted list of edges
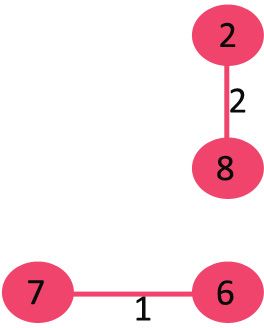
1.   Pick edge 7-6:  No cycle is formed, include it.

2. Pick edge 8-2: No cycle is formed, include it.

3.   Pick edge 6-5:  No cycle is formed, include it.

4. Pick edge 0-1: No cycle is formed, include it.

5. Pick edge 2-5: No cycle is formed, include it.

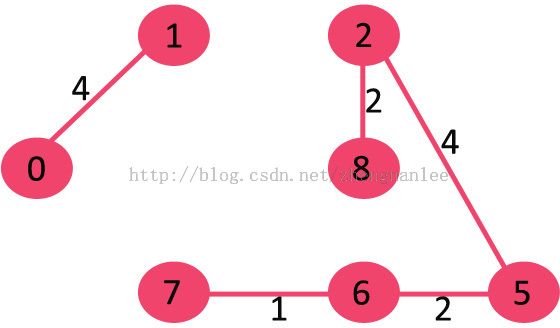
6. Pick edge 8-6: Since including this edge results in cycle, discard it.

7. Pick edge 2-3: No cycle is formed, include it.

 

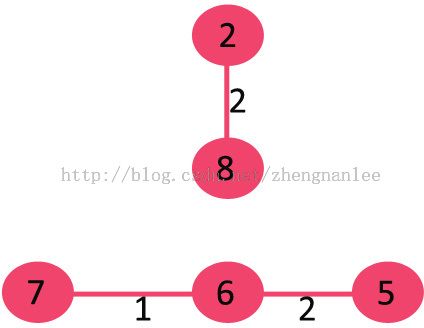
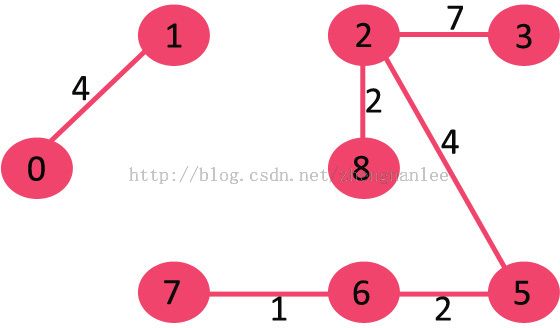
8. Pick edge 7-8: Since including this edge results in cycle, discard it.

9. Pick edge 0-7: No cycle is formed, include it.

 

10. Pick edge 1-2: Since including this edge results in cycle, discard it.

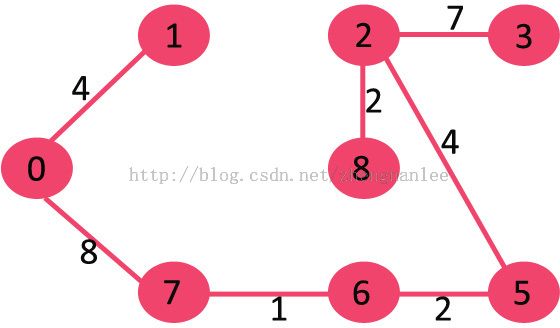
11. Pick edge 3-4: No cycle is formed, include it.

Since the number of edges included equals (V – 1), the algorithm stops here.

Here is the source code demonstrating the procedure.

 

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// a structure to represent a weighted edge in graph
struct Edge
{
    int src, dest, weight;
};

// a structure to represent a connected, undirected and weighted graph
struct Graph
{
    // V-> Number of vertices, E-> Number of edges
    int V, E;

    // graph is represented as an array of edges. Since the graph is
    // undirected, the edge from src to dest is also edge from dest
    // to src. Both are counted as 1 edge here.
    struct Edge* edge;
};

// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
    struct Graph* graph = (struct Graph*) malloc( sizeof(struct Graph) );
    graph->V = V;
    graph->E = E;

    graph->edge = (struct Edge*) malloc( graph->E * sizeof( struct Edge ) );

    return graph;
}

// A structure to represent a subset for union-find
struct subset
{
    int parent;
    int rank;
};

// A utility function to find set of an element i
// (uses path compression technique)
int find(struct subset subsets[], int i)
{
    // find root and make root as parent of i (path compression)
    if (subsets[i].parent != i)
        subsets[i].parent = find(subsets, subsets[i].parent);

    return subsets[i].parent;
}

// A function that does union of two sets of x and y
// (uses union by rank)
void Union(struct subset subsets[], int x, int y)
{
    int xroot = find(subsets, x);
    int yroot = find(subsets, y);

    // Attach smaller rank tree under root of high rank tree
    // (Union by Rank)
    if (subsets[xroot].rank < subsets[yroot].rank)
        subsets[xroot].parent = yroot;
    else if (subsets[xroot].rank > subsets[yroot].rank)
        subsets[yroot].parent = xroot;

    // If ranks are same, then make one as root and increment
    // its rank by one
    else
    {
        subsets[yroot].parent = xroot;
        subsets[xroot].rank++;
    }
}

// Compare two edges according to their weights.
// Used in qsort() for sorting an array of edges
int myComp(const void* a, const void* b)
{
    struct Edge* a1 = (struct Edge*)a;
    struct Edge* b1 = (struct Edge*)b;
    return a1->weight > b1->weight;
}

// The main function to construct MST using Kruskal's algorithm
void KruskalMST(struct Graph* graph)
{
    int V = graph->V;
    struct Edge result[V];  // Tnis will store the resultant MST
    int e = 0;  // An index variable, used for result[]
    int i = 0;  // An index variable, used for sorted edges

    // Step 1:  Sort all the edges in non-decreasing order of their weight
    // If we are not allowed to change the given graph, we can create a copy of
    // array of edges
    qsort(graph->edge, graph->E, sizeof(graph->edge[0]), myComp);

    // Allocate memory for creating V ssubsets
    struct subset *subsets =
        (struct subset*) malloc( V * sizeof(struct subset) );

    // Create V subsets with single elements
    for (int v = 0; v < V; ++v)
    {
        subsets[v].parent = v;
        subsets[v].rank = 0;
    }

    // Number of edges to be taken is equal to V-1
    while (e < V - 1)
    {
        // Step 2: Pick the smallest edge. And increment the index
        // for next iteration
        struct Edge next_edge = graph->edge[i++];

        int x = find(subsets, next_edge.src);
        int y = find(subsets, next_edge.dest);

        // If including this edge does't cause cycle, include it
        // in result and increment the index of result for next edge
        if (x != y)
        {
            result[e++] = next_edge;
            Union(subsets, x, y);
        }
        // Else discard the next_edge
    }

    // print the contents of result[] to display the built MST
    printf("Following are the edges in the constructed MST\n");
    for (i = 0; i < e; ++i)
        printf("%d -- %d == %d\n", result[i].src, result[i].dest,
                                                   result[i].weight);
    return;
}

// Driver program to test above functions
int main()
{
    /* Let us create following weighted graph
             10
        0--------1
        |  \     |
       6|   5\   |15
        |      \ |
        2--------3
            4       */
    int V = 4;  // Number of vertices in graph
    int E = 5;  // Number of edges in graph
    struct Graph* graph = createGraph(V, E);


    // add edge 0-1
    graph->edge[0].src = 0;
    graph->edge[0].dest = 1;
    graph->edge[0].weight = 10;

    // add edge 0-2
    graph->edge[1].src = 0;
    graph->edge[1].dest = 2;
    graph->edge[1].weight = 6;

    // add edge 0-3
    graph->edge[2].src = 0;
    graph->edge[2].dest = 3;
    graph->edge[2].weight = 5;

    // add edge 1-3
    graph->edge[3].src = 1;
    graph->edge[3].dest = 3;
    graph->edge[3].weight = 15;

    // add edge 2-3
    graph->edge[4].src = 2;
    graph->edge[4].dest = 3;
    graph->edge[4].weight = 4;

    KruskalMST(graph);

    return 0;
}