word2vec之一发入魂（1）：CBOW, Skip-gram原理详解

1 摘要

在自然语言处理中，计算机往往难以处理复杂的文字系统。因此，如何把“文字”转换成计算机易处理的形式成为了一个亟需解决的问题。为解决这一问题，word2vec提出了一种把“词”映射到实数域向量的思路。其中这个转换过程被称为word embedding，转换出来的向量也叫词向量。本文将从原理上简要介绍word2vec模型中包含的两个经典算法：CBOW与Skip-gram模型，并对两者的相同点，不同点作分析。

2 word2vec 简介

word2vec的目的是根据具体任务，把 “词”转换成合适的向量（也就是说同一个词，在新闻类任务和在散文类任务中的向量表示可能是不一样）。通常的做法是，把每一个词对应的词向量$v_i$作为模型的训练参数，然后通过一定的规则对模型进行训练，最终得到的参数矩阵就是词向量。

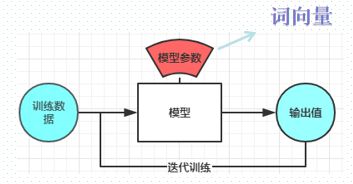
注：这个地方与分类任务有点不一样，分类任务是希望通过模型来预测分类，目的获取模型的输出结果，而word2vec目的是获取模型的训练参数。

3 one-hot编码

在介绍CBOW与Skip-gram模型之前有必要介绍一下one-hot编码。one-hot编码的原理很简单，它让每一个词占一个维度，如果该词出现了，则该维度的值为1，其余维度的值为0。举个例子，假设我们的语言中只有三个词，分别是“who”，“are”，“you”，那么根据编码规则会有以下编码：

词	向量
who	[1,0,0]
are	[0,1,0]
you	[0,0,1]

虽然one-hot编码的原理简单，却在实践中很少被运用，原因有二：

1. 维度爆炸：从上面的例子来看，每个词被编码成3维的向量，可见编码的维度取决于词库中词的数目。在实际应用中，大规模的词库往往会导致维度爆炸的问题。
2. 完全割裂了词与词之间的联系：one-hot编码的编码方式使得两词之间相互正交（词向量内积永远为0），因此无法保留两词之间的相关性，这说明这编码方式的表达能力并不强。如 nice和good在语义上是应该有较高的相关，而nice和bike之间应该具有较低的相关性。

为了改善上述两个缺点，word2vec提出了CBOW与Skip-gram模型。

4 Skip-gram模型

4.1 原理推导

Skip-gram模型利用中心词来生成周边的词。假设有一句子：·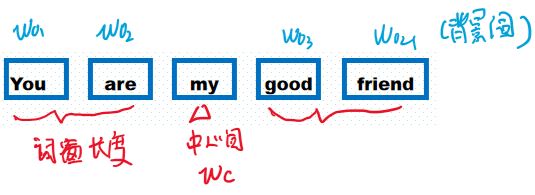
为了用$w_c$预测词窗中的背景词$w_o$，Skip-gram首先利用条件概率对$w_c$，$w_o$进行建模，即$$P(\text{“you"},\text{“are"},\text{“good"},\text{“friend"}\mid \text{“my"}).$$
假设背景词之间相互独立（类似于朴素贝叶斯模型中的假设条件），可以把上述概率写成：

$$P(\text{“You"}\mid \text{“my"})\cdot P(\text{“are"}\mid \text{“my"})\cdot P(\text{“good"}\mid \text{“my"})\cdot P(\text{“friend"}\mid \text{“my"}).$$
其中，$w_c$与$w_o$的表达式为：
$$P(w_o\mid w_c)=\frac{\text{exp}({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)},$$

在skip-gram模型中，一个词往往会保存两种形式的向量，一个是作为中心词的向量（用$v$表示），一个是作为背景的向量（用$u$来表示）。上式本质上是一个softmax的表达式，其中$u_o$表示背景词的背景向量，$v_c$表示中心词的中心词向量，$V$表示整个词库集合。注：训练好的词库会用中心词向量来代表一个词。

接下来我们来思考一个问题：为什么要用这种形式来表示条件概率？

首先，要构造出$P(w_o\mid w_c)$，就需要考虑中心词与背景词之间的相关性。这个式子中的内积部分，实质上就是计算中心词与背景词的相似度。其次，softmax相当于把相似度占比映射到了[0,1]的概率上，因此保证了$P(w_o\mid w_c)$的合法性（求和为1）。

最后，结合上述的表达式子，可以得出对于一个单词$t$目标函数：

4.2 训练

训练Skip-gram模型时一般采用随机梯度下降法（Stochastic gradient descent, SGD）来优化目标函数。优化过程一般如下图所示：

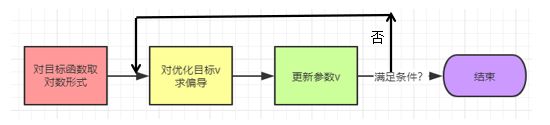
具体公式如下：

5. CBOW

5.1 原理

CBOW模型全称为Continuous Bag-of-Words Model。与Skip-gram利用中心词预测周边词的做法不同，CBOW则是利用上下文信息来预测中心词。同样用一个句子为例，此时$w_c$是被预测的词。

则条件概率公式被转化为：
$$P(\text{“my"}\mid \text{“you"},\text{“are"},\text{“good"},\text{“friend"}).$$
在掌握了Skip-gram之后，对CBOW进行原理推荐也就比较简单。首先对背景词，中心词进行条件概率建模：

$$P(w_c\mid w_{o_1},\dots ,w_{o_{2m}})=\frac{\text{exp}\left(\frac{1}{2m}{\mathbf{u}}_c^{\top }({\mathbf{v}}_{o_1}+\dots +{\mathbf{v}}_{o_{2m}})\right)}{{\sum }_{i\in \mathcal{V}}\text{exp}\left(\frac{1}{2m}{\mathbf{u}}_i^{\top }({\mathbf{v}}_{o_1}+\dots +{\mathbf{v}}_{o_{2m}})\right)}.$$

注意这里是对中心词的背景向量（$u$）与背景词的中心向量（$v$）之和做点积，这里笔者理解为是 “联系上下文” 的一种体现。

5.2 训练

训练的流程与Skip-gram一致，只是目标函数有所调整。

预测词库中任一单词的概率表达：
$$\prod _{t=1}^{T}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)}).$$

为了让符号更加简单，我们记${\mathcal{W}}_o=\{w_{o_1},\dots ,w_{o_{2m}}\}$，且${\bar{\mathbf{v}}}_o=\left({\mathbf{v}}_{o_1}+\dots +{\mathbf{v}}_{o_{2m}}\right)/(2m)$，那么上式可以简写成

$$P(w_c\mid {\mathcal{W}}_o)=\frac{\exp \left({\mathbf{u}}_c^{\top }{\bar{\mathbf{v}}}_o\right)}{{\sum }_{i\in \mathcal{V}}\exp \left({\mathbf{u}}_i^{\top }{\bar{\mathbf{v}}}_o\right)}.$$

得到优化表达式后，可以开始进行SGD：
step1：取对数
$$-\sum _{t=1}^T\text{log}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)}).$$

step2:计算梯度
$$\frac{\partial \log P(w_c\mid {\mathcal{W}}_o)}{\partial {\mathbf{v}}_{o_i}}=\frac{1}{2m}\left({\mathbf{u}}_c-\sum _{j\in \mathcal{V}}\frac{\exp ({\mathbf{u}}_j^{\top }{\bar{\mathbf{v}}}_o){\mathbf{u}}_j}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\bar{\mathbf{v}}}_o)}\right)=\frac{1}{2m}\left({\mathbf{u}}_c-\sum _{j\in \mathcal{V}}P(w_j\mid {\mathcal{W}}_o){\mathbf{u}}_j\right).$$

6. CBOW与Skip-gram对比

角度1：复杂度–Skip-gram的训练时间要更长

CBOW： 计算复杂度为O(V)。算法是用背景词来预测中心词，因此一个窗口只需要预测一次。
Skip-gram: 计算复杂度为O(KV)。利用中心词来预测周围的k个词，相当于一个窗口要预测k次。

相同处：观察两个算法的梯度下降公式，可以发现单词的梯度计算都与词库的规模有关，词库越大，计算量越大。

角度2：准度

Skip-gram有一个优点：==在样本数量不大的情况下，对生僻字生僻字的描述会更准确。==因为Skip-gram是不断用周围的词来预测中间的词，这就说明中间词会被集中调整多次。具体来说，中心词会在一个词窗口中被更新k次，当然精度会有所提升（一个学生K个老师）。

另一方面，观察CBOW中的梯度下降表达式中${\bar{\mathbf{v}}}_o=\left({\mathbf{v}}_{o_1}+\dots +{\mathbf{v}}_{o_{2m}}\right)/(2m)$，这表示梯度下降是在对背景词向量求和的情况下进行的，说明优化的效果被分摊到了其他词上去，就类似于一个老师要教K个学生，肯定没有K个老师教一个学生那么有针对性。

7. 总结

1. one-shot编码有两个弊端：维度爆炸与丢失单词间的相关性
2. word2vec有点类似于自动编码器，焦点在于模型参数而不是模型的输出。
3. skip-gram的计算复杂度更高，在样本不多的情况下对生僻字的表达效果更好。
4. 如果使用梯度下降法进行优化，skip-gram与cbow梯度计算代价与词库的规模$V$有关

参考：
B站MXnet教学视频
cbow 与 skip-gram的比较
word2vec原论文：Efficient Estimation of Word Representations in Vector Space