C++STL详解(七)——priority_queue的使用和模拟实现
文章目录
- priority_queue的使用
-
-
- priority_queue的介绍
- priority_queue的定义方式
- priority_queue各个接口的使用
-
- priority_queue的模拟实现
-
-
- 堆的向上调整
- 堆的向下调整
- 迭代器区间构造
- 仿函数
- priority_queue的模拟实现完整代码
-
priority_queue的使用
priority_queue的介绍
优先级队列默认使用vector作为底层的存储的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priorityda_queue。
注意:
默认情况下priority_queue是大堆。
priority_queue的定义方式
方式一:
使用的是vector作为底层存储容器,内部为构造为大堆结构。
//大堆
priority_queue<int, vector<int>, less<int>> q1;
方式二:
使用vector作为底层容器,内部构造为小堆结构。
//小堆
priority_queue<int, vector<int>, greater<int>> q2;
方式三:
不指定底层容器和内部构造的大小堆结构,此时编译器默认使用构造大堆结构。
priority_queue<int> q;
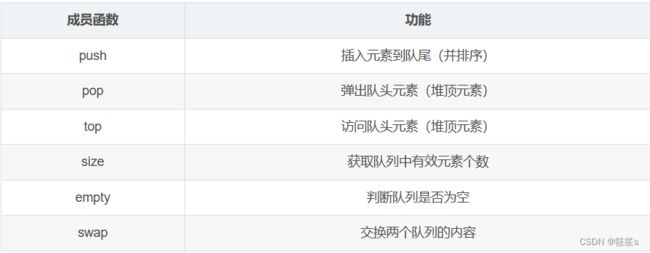
priority_queue各个接口的使用
例如:
int main()
{
priority_queue<int> q1;
q1.push(3);
q1.push(1);
q1.push(2);
q1.push(4);
q1.push(6);
q1.push(5);
while (!q1.empty())
{
cout << q1.top() << " ";
q1.pop();
}
q1.push(1);
cout << q1.size() << endl;
}
priority_queue的模拟实现
我们知道priority_queue的底层实际上就是堆,所以我们必须先了解一下堆的两种调整。
堆的向上调整
时间复杂度:
O(n) = log(n)
基本思路:
在大根堆的情况下:
1:传孩子,求父亲。
2: 如果子结点大于父亲结点,就交换子节点与它的父节点的位置,此时子节点就等于原来父亲的结点。
3: 然后又通该子节点向上求得它的父节点,进行循环比较父子结点的大小。
4: 当子节点为0时,就已经与跟结点交换了,循环结束。( 不能使用parent>=0这个条件,当parent = 0,父子结点交换后,此时再计算parent时取整还是等于0,不可能为负数,此时便会无限循环。)
堆的向上调整代码:
void AdjustUp( size_t child )
{
size_t parent = ( child - 1 ) / 2;
while ( child > 0 )
{
if( _con[parent] < _con[child] )
{
swap( _con[parent],_con[child]);
child = parent;
parent = ( child -1 ) / 2;
}
//如果子节点不大于父节点,就不用交换了。
else
{
break;
}
}
}
堆的向下调整
时间复杂度;
log(n)
基本思路:
在大根堆的情况下:
1: 传父亲,求孩子。
2:我们先要求父亲中左右孩子最大的那一个。
注意:使用[]比较时最好先判断一下右孩子必须在的情况。
3: 循环两个步骤: 一直循环的最好情况就是孩子没有超过最后一个数的下标。
如果选出的孩子大于父亲,就交换,并且原来孩子的下标等于父亲的下标。
如果左右孩子都不大于父亲,就说明不用交换,向下调整成功。
void adjust_down ( size_t parent)
{
//求出左孩子下标
size_t child = parent* 2 + 1;
while( child < _con.size() )
{
//有了右孩子才可以左右孩子比较。
if( child + 1 < _con.size() && _con[child]< _con[child+1])
{
child++;
}
if( _con[parent] < _con[child] )
{
swap( _con[parent], _con[child]);
parent = child;
child = parent* 2 + 1;
}
else
{
break;
}
}
}
迭代器区间构造
时间复杂度:
Nlog(N)
先插入对应的迭代器区间,然后从最后一个数据的父节点开始向下建堆。
template< InputIterator >
priority_queue( InputIterator first, InputIterator last )
{
while( first != last )
{
_con.push_back(*first);
++first;
}
for ( int i = ( _con.size() - 1 - 1 / 2; i >= 0 ; -- i )
{
adjust_down();
}
}
仿函数
调用仿函数时,就像调用lsFunc.operator()(1,2)一样。用来比较大小。
template<T>
class Less
{
public:
bool operator()( const T& l, const T& r )
{
return l < r;
}
};
template<T>
class greater
{
public:
bool operator()( const T& l,const T& r )
{
return l > r;
}
};
less<int> lsFunc;
cout << lsFunc(1, 2) << " ";
priority_queue的模拟实现完整代码
namespace yzh
{
//模板参数代表的类型,根据实参转换为对应的类型。
template < class T, Container = vector<T>, class Compare = std:: greater(T) >
class priority_queue
{
public:
//显示写了,会通过初始化列表在初始化列表内进行初始化,或者调用默认构造。
priority_queue()
{
}
template<class InputIterator>
priority_queue(InputIterator first, InputIterator last)
{
while (first != last)
{
_con.push_back(*first);
}
for( int i = ( _con.size() -1 -1 ) /2;i >= 0; --i )
{
adjust_down();
}
}
void push( const T& x )
{
_con.push_back(x);
adjust_up(_con.size() -1 );
}
//堆的删除是将第一个数据与最后一个元素进行交换,再将最后一个元素删除。
//然后再用向下调整的方式调整堆顶。
void pop ()
{
std::swap( _con[0], _con[_con.size() - 1 ] );
_con.pop_back();
adjust_down();
}
//堆顶只可读不可以修改。
const T top() const
{
assert(!empty() );
return_con[0];
}
size_t size() const
{
return _con.size();
}
bool empty() const
{
return _con.empty();
}
private:
Container _con;
}
}