数据结构(Java)---栈
1.简介
栈是一种只能在一端进行插入(入栈)或删除(出栈)的线性表,表中运行进行插入,删除的一端为栈顶,另一端为栈底。
栈的特点是先进后出 ,每次后进栈的元素先出栈,每次进栈的数据元素都放在栈顶充当新的栈顶元素,栈也被称为后进先出表。栈也分为顺序栈和链栈。
2.顺序栈
2.1简介
顺序栈主要是采用顺序存储结构来存储数据,和线性表一样,线性表也分为顺序表和链表,而栈也有顺序栈,通常使用数组来实现。
2.2 相关操作

如上所示,我们可以使用一个指针(变量)top == -1来判断栈空,当我们把元素进栈时,让top加1往上移,然后将元素放进去,如果元素想要出栈的话,将top里的值取出来,然后让top减1。
在顺序栈里,通常使用top==-1来表示栈底或栈空,使用top==(数组大小)-1来代表栈满了,顺序栈可以使用数组的方式来实现。
2.3 代码实现
package Structures;
import java.util.Scanner;
public class ArrayStack {
public static void main(String[] args) {
Stack stack = new Stack(4);
String key;
boolean loop = true;
Scanner scanner = new Scanner(System.in);
while (loop){
System.out.println("show: 遍历栈");
System.out.println("exit: 退出栈");
System.out.println("push: 入栈");
System.out.println("pop: 出栈");
System.out.println("请选择相关操作");
while (loop){
key = scanner.next();
switch (key){
case "show":
stack.list();
break;
case "exit":
scanner.close();
loop = false;
break;
case "push":
System.out.println("请输入值:");
int i = scanner.nextInt();
stack.push(i);
break;
case "pop":
try{
int pop = stack.pop();
System.out.print(pop);
}catch (Exception e){
System.out.println(e.getMessage());
}
break;
}
}
}
}
}
class Stack {
private int maxSize;
private int[] stack;
private int top = -1;
public Stack(int maxSize) {
this.maxSize = maxSize;
stack = new int[maxSize];
}
//判断栈空
public boolean isFull() {
return top == maxSize - 1;
}
//判断栈满
public boolean isEmpty() {
return top == -1;
}
//入栈
public void push(int value) {
if (isFull()) {
System.out.println("栈已满");
}
top++;
stack[top] = value;
}
//出栈
public int pop() {
if (isEmpty()) {
throw new RuntimeException("栈空,无数据");
}
int value = stack[top];
top--;
return value;
}
//遍历栈
public void list() {
if (isEmpty()) {
System.out.println("栈空,无数据");
return;
}
for (int i = top; i >=0 ; i--) {
System.out.println(stack[i]);
}
}
}
3.链栈
3.1 简介
链栈,顾名思义就是使用链表结构来实现的栈,可以理解为结点的先进后出的链表。
3.2 相关操作
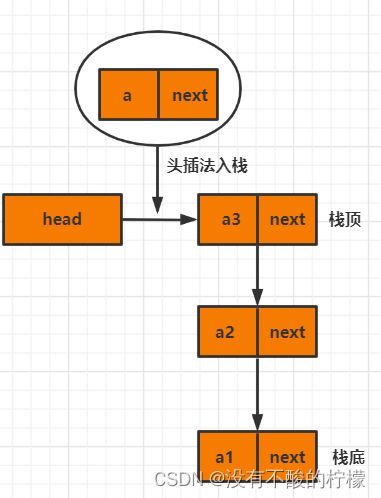
在链表中,有头插法的结点插入法,我们可以使用头插法(入栈)来创建链表,然后删除结点(出栈)时删除删除头结点后面的即可。
3.3 代码实现
package Structures;
import java.util.Scanner;
public class LinkedStack {
public static void main(String[] args) {
LStackOperation operation = new LStackOperation();
operation.push(new LStack(1));
operation.push(new LStack(2));
operation.push(new LStack(3));
operation.list();
System.out.println("出栈后:");
operation.pop();
operation.pop();
operation.list();
}
}
class LStack{
private Object data;
private LStack next;
public LStack(Object data) {
this.data = data;
}
public Object getData() {
return data;
}
public void setData(Object data) {
this.data = data;
}
public LStack getNext() {
return next;
}
public void setNext(LStack next) {
this.next = next;
}
}
class LStackOperation{
//头结点
public LStack head = new LStack("");
//判断栈是否为空
public boolean isEmpty(){
return head == null;
}
//入栈
public void push(LStack num){
LStack temp = head;
num.setNext(temp.getNext());
temp.setNext(num);
}
//出栈
public void pop(){
LStack temp = head;
if(temp.getNext() == null){
System.out.println("栈已空");
}
temp.setNext(temp.getNext().getNext());
}
//遍历栈
public void list(){
LStack temp = head.getNext();
while (temp != null){
System.out.println(temp.getData());
temp = temp.getNext();
}
}
}
4.栈的常见场景(表达式运算)
4.1 中缀表达式
概述: 中缀表达式是我们在日常生活中常见的表达式,如:(3+4)*5-6,中缀表达式是表达式的运算符在值的中间,相对于人来说,中缀表达式的运算是简单的,但对于计算机来说就比较麻烦,因为不仅要考虑到先加减后乘除,还要考虑到括号的问题。
解决思路: 定义两个栈,一个数栈(专门用来存储数字)和一个符号栈(专门用来存储符号)配合完成。
1.定义一个index值来遍历表达式
2.当发现是一个数字时,则直接进入数栈(要注意多位数,可以使用一个变量来进行拼接)
3.当发现是一个符号时,则直接进入符号栈
3.1如果符号栈为空,则直接入栈
3.2如果符号栈有符号时,首先比较当前操作符和栈顶符号的优先级,如果当前操作符优先级小于或等于栈顶的符号时,从数栈中出栈两个数和从符号栈出一个符号进行运算,然后将结果入数栈,如果优先级大于的话就直接入栈
4.当表达式扫描完毕后,就开始出栈进行运算,直到得出最后结果
代码实现:
package Structures;
public class Calculator {
public static void main(String[] args) {
String expression = "7+2*6-4";
//创建两个栈
Stack2 numStack = new Stack2(10);
Stack2 operStack = new Stack2(10);
int index = 0; //索引,遍历表达式
int num1 = 0; //数字1
int num2 = 0; //数字2
int oper = 0; //操作符
int res = 0; //结果
char ch = ' ';
while (true) {
//获取字符
ch = expression.substring(index, index + 1).charAt(0);
//判断
if (operStack.isOper(ch)) {
//符号栈有值
if (!operStack.isEmpty()) {
//优先级小于或等于
if (operStack.priority(ch) <= operStack.priority(operStack.peek())) {
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
//将结果入栈
numStack.push(res);
//将当前操作符入栈
operStack.push(ch);
} else {
//优先级大于的话,直接入栈
operStack.push(ch);
}
} else {
//为空直接入栈
operStack.push(ch);
}
} else {
//不是符号就是数字(阿斯托吗值-48,得到相应的数字)
numStack.push(ch - 48);
}
index++;
if (index >= expression.length()) {
break;
}
}
//扫描完毕,开始执行栈中的运算
while (true) {
if (operStack.isEmpty()) {
break;
}
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
numStack.push(res);
}
System.out.println(numStack.pop());
}
}
class Stack2 {
private int maxSize;
private int[] stack;
private int top = -1;
public Stack2(int maxSize) {
this.maxSize = maxSize;
stack = new int[maxSize];
}
//查看栈顶元素
public int peek() {
return stack[top];
}
//判断栈空
public boolean isFull() {
return top == maxSize - 1;
}
//判断栈满
public boolean isEmpty() {
return top == -1;
}
//入栈
public void push(int value) {
if (isFull()) {
System.out.println("栈已满");
}
top++;
stack[top] = value;
}
//出栈
public int pop() {
if (isEmpty()) {
throw new RuntimeException("栈空,无数据");
}
int value = stack[top];
top--;
return value;
}
//遍历栈
public void list() {
if (isEmpty()) {
System.out.println("栈空,无数据");
return;
}
for (int i = top; i >= 0; i--) {
System.out.println(stack[i]);
}
}
// 判断运算符优先级(假设表达式只有+-*/)
public int priority(int oper) {
if (oper == '*' || oper == '/') {
return 1;
} else if (oper == '+' || oper == '-') {
return 0;
} else {
return -1;
}
}
//判断是否是一个运算符
public boolean isOper(char val) {
return val == '+' || val == '-' || val == '*' || val == '/';
}
//计算
public int cal(int num1, int num2, int oper) {
int res = 0;
switch (oper) {
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1;
break;
case '*':
res = num1 * num2;
break;
case '/':
res = num2 / num1;
break;
}
return res;
}
}
4.2 前缀表达式
概述: 前缀表达式主要是将表达式的运算符放在数值的前面,然后计算机根据前缀表达式来进行运算,在前缀表达式中,计算机不用考虑运算符优先级问题,因为在中缀表达式转为前缀表达式时,运算符的优先级已经处理好了的。比如说:7+2x6-4的前缀表达式为:-+7x264。
中缀转前缀的过程:首先按照中缀的运算规则,2x6优先,则是x26,然后7+x26的话就是+7x26,接下来是+7x26-4的话就是-+7x264。
解决思路: 从右至左扫描前缀表达式,遇到数字时将数字入栈,遇到运算符时,出栈两个数字进行运算并将结果入栈,然后一直重复得出最后结论。
4.3 后缀表达式
概述: 后缀表达式则是符号位在运算数字后面,也被称为逆波兰表达式,在表达式的运算中,大多数都是采用逆波兰表达式来运算。
解决思路: 和前缀表达式类似,只不过后缀表达式是从左至右扫描,更加合理。
中缀转后缀思路:
1.初始化两个栈,一个符号栈s1和一个存储中间结果栈s2
2.从左到右扫描中缀表达式
3.遇到数字,直接入栈s2
4.遇到符号,比较其与s1栈顶运算符的优先级:
4.1:如果s1为空,或栈顶运算符为(,或者优先级比栈顶的高,则直接入栈
4.2:否则的话景s1栈顶的运算符弹出并压入s2,然后继续执行4.1
5.遇到括号的话:
5.1:如果是(,直接入栈s1
5.2:如果是),则依次弹出s1栈顶的运算符,直到遇到),当遇到)时,直接去掉这一堆括号
6.重复执行2~5,直到表达式最右边
7.然后将s1中剩余的运算符压入s2
8.然后弹出s2的值,然后值反转就是后缀表达式
代码实现: 代码实现部分暂时没考虑到表达式的小数点等问题。
package Structures;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class BLCalculator {
public static void main(String[] args) {
String expression = "1+((2+3)x4)-5";
List<String> list = getList(expression);
System.out.println(list);
List<String> list1 = TransferList(list);
System.out.println(list1);
int calculator = calculator(list1);
System.out.println(calculator);
}
//获取字符串信息
/* public static List getList(String expression) {
//分割字符串(字符串带空格)
String[] s = expression.split(" ");
ArrayList arrayList = new ArrayList<>();
for (String temp : s
) {
arrayList.add(temp);
}
return arrayList;
}*/
//表达式拆分
public static List<String> getList(String s) {
ArrayList<String> list = new ArrayList<>();
int i = 0;
String temp;
char c;
do {
//非数字,ASCII值(0~9为48~57)
if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
list.add("" + c);
i++;
} else {
//如果是数字,考虑多位数的问题(如果是数字,遍历表达式,拼接数字,直到遇到符号)
temp = "";
while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
temp += c;
i++;
}
list.add(temp);
}
} while (i < s.length());
return list;
}
//中缀转后缀
/*
* 1.初始化两个栈,一个符号栈s1和一个存储中间结果栈s2
2.从左到右扫描中缀表达式
3.遇到数字,直接入栈s2
4.遇到符号,比较其与s1栈顶运算符的优先级:
4.1:如果s1为空,或栈顶运算符为(,或者优先级比栈顶的高,则直接入栈
4.2:否则的话景s1栈顶的运算符弹出并压入s2,然后继续执行4.1
5.遇到括号的话:
5.1:如果是(,直接入栈s1
5.2:如果是),则依次弹出s1栈顶的运算符,直到遇到),当遇到)时,直接去掉这一堆括号
6.重复执行2~5,直到表达式最右边
7.然后将s1中剩余的运算符压入s2
8.然后弹出s2的值,然后值反转就是后缀表达式*/
public static List<String> TransferList(List<String> list) {
//定义两个栈
Stack<String> s1 = new Stack<>();
Stack<String> s2 = new Stack<>();
//开始遍历
for (String item : list
) {
//如果是数字,直接入栈
if (item.matches("\\d+")) {
s2.add(item);
} else if (item.equals("(")) {
s1.push(item);
} else if (item.equals(")")) {
//如果是),则依次弹出s1栈顶的运算符,直到遇到),当遇到)时,直接去掉这一堆括号
while (!s1.peek().equals("(")) {
s2.add(s1.pop());
}
s1.pop();//弹出小括号
} else {
//判断符号优先级
while (s1.size() != 0 && priority(s1.peek()) >= priority(item)) {
s2.add(s1.pop());
}
s1.push(item);
}
}
//遍历结束,开始将s1剩余的符号出栈并入栈s2
while (s1.size() != 0) {
s2.add(s1.pop());
}
return s2;
}
//逆波兰计算(从左到右扫描,遇到数字直接入栈,遇到符号,出栈两个数字计算,然后将结果入栈,继续计算)
public static int calculator(List<String> ls) {
Stack<String> stack = new Stack<>();
for (String items : ls
) {
//正则表达式(匹配多位数)
if (items.matches("\\d+")) {
stack.push(items);
} else {
//符号
int num1 = Integer.parseInt(stack.pop());
int num2 = Integer.parseInt(stack.pop());
int res = 0;
if (items.equals("+")) {
res = num1 + num2;
} else if (items.equals("-")) {
res = num2 - num1;
} else if (items.equals("x")) {
res = num1 * num2;
} else if (items.equals("/")) {
res = num2 / num1;
}
stack.push(String.valueOf(res));
}
}
return Integer.parseInt(stack.pop());
}
//比较符号优先级
public static int priority(String oper) {
if (oper.equals("x") || oper.equals("/")) {
return 1;
} else if (oper.equals("+") || oper.equals("-")) {
return 0;
} else {
return -1;
}
}
}