详解二叉树的三种遍历方式(递归、迭代、Morris算法)
详解二叉树的三种遍历方式(递归、迭代、Morris算法)
最重要的事情写在前面:遍历顺序不一定就是操作顺序!!!
递归解法
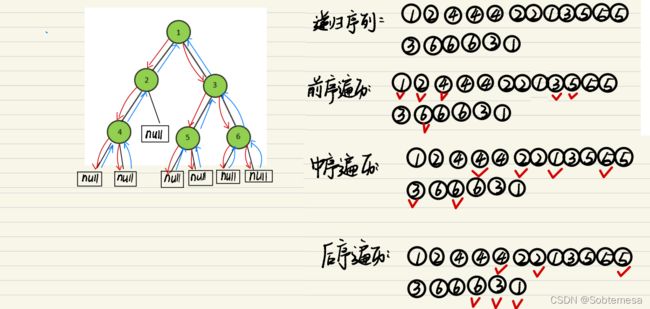
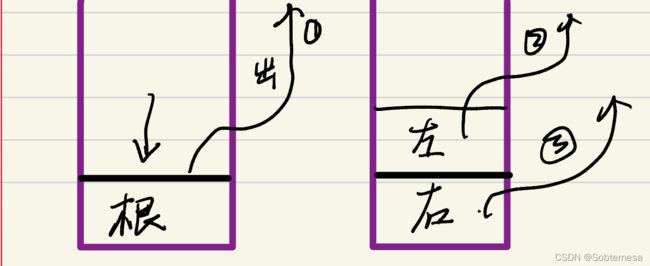
首先,一颗二叉树它的递归序列是一定的,导致其前中后序不同的原因只不过是访问节点的时机不同。
递归序列:1 2 4 4 4 2 2 1 3 5 5 5 3 6 6 6 3 1
a:先序:第一次来到自己打印。1 2 4 3 5 6
b:中序:第二次来到自己打印。4 2 1 5 3 6
c:后序:第三次来到自己打印。4 2 5 3 6 1
代码:(前序–中序–后序)
/**
* 前序遍历递归
* @param root
*/
public void preOrder(BTNode root){
if(root==null){
System.out.print("NULL->");
return;
}
//第一次来到此节点
System.out.print(root.val+"->");
preOrder(root.left);
preOrder(root.right);
}
/**
* 中序遍历递归
* @param root
*/
public void InOrder(BTNode root){
if(root==null){
System.out.print("NULL->");
return;
}
InOrder(root.left);
//第二次来到此节点
System.out.print(root.val+"->");
InOrder(root.right);
}
/**
* 后序遍历递归
* @param root
*/
public void PostOrder(BTNode root){
if(root==null){
System.out.print("NULL->");
return;
}
PostOrder(root.left);
PostOrder(root.right);
//第三次来到此节点
System.out.print(root.val+"->");
}
迭代解法
递归的实现就是:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归为什么可以返回上一层位置的原因。
此时大家应该知道我们用栈也可以是实现二叉树的前后中序遍历了。
递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其余的实现与细节都相同。
前序遍历:
解法一:
/**
* 前序遍历迭代
* @param root
*/
public List<Integer> preOrder3(BTNode root){
Stack<BTNode> stack=new Stack<>();
List<Integer> res = new ArrayList<Integer>();
BTNode cur=root;
if(root==null){
return res;
}
// cur不为null时入栈,向left方向推进直到叶子节点
while(cur!=null){
stack.push(cur);
res.add(cur.val);
cur=cur.left;
}
while (!stack.empty()){
// 向left推进到叶子节点后弹出该叶子节点
BTNode top=stack.pop();
// 左子树遍历完毕,回到该节点,向right推进.
cur=top.right;
}
return res;
}
也可以写成这样:
/**
* 前序遍历迭代
* @param root
* @return
*/
public List<Integer> preOrder3(BTNode root){
Stack<BTNode> stack=new Stack<>();
List<Integer> res = new ArrayList<Integer>();
BTNode cur=root;
if(root==null){
return res;
}
// 同时满足root为null及stack为空,才将结果返回
while (!stack.empty()||cur!=null){
// cur不为null时入栈,向left方向推进直到叶子节点
while(cur!=null){
stack.push(cur);
res.add(cur.val);
cur=cur.left;
}
// 向left推进到叶子节点后弹出该叶子节点
BTNode top=stack.pop();
// 左子树遍历完毕,回到该节点,向right推进.
cur=top.right;
}
return res;
}
解法二:
首先我们应该创建一个Stack用来存放节点,首先我们想要打印根节点的数据,此时Stack里面的内容为空,所以我们优先将头结点加入Stack,然后打印。
之后我们应该先打印左子树,然后右子树。所以先加入Stack的就是右子树,然后左子树。
此时你能得到的流程如下:
/**
* 前序遍历迭代
* @param root
*/
public List<Integer> preOrder2(BTNode root){
Stack<BTNode> stack=new Stack<>();
List<Integer> res = new ArrayList<Integer>();
if(root!=null){
stack.push(root);
}
while (!stack.empty()){
BTNode top=stack.pop();
res.add(top.val);
if(top.right!=null)stack.push(top.right);
if(top.left!=null)stack.push(top.left);
}
return res;
}
中序遍历:像递归一样,在前序遍历的基础上稍作修改即可。
/**
* 前序遍历迭代
* @param root
*/
public List<Integer> preOrder3(BTNode root){
Stack<BTNode> stack=new Stack<>();
List<Integer> res = new ArrayList<Integer>();
BTNode cur=root;
if(root==null){
return res;
}
// cur不为null时入栈,向left方向推进直到叶子节点
while(cur!=null){
stack.push(cur);
cur=cur.left;
}
while (!stack.empty()){
// 向left推进到叶子节点后弹出该叶子节点
BTNode top=stack.pop();
res.add(top.val);
// 左子树遍历完毕,回到该节点,向right推进.
cur=top.right;
}
return res;
}
后序遍历:
对于迭代的操作,则后续遍历稍显麻烦。
因为左 -> 右 -> 中 的访问过程中当遍历到最左边,如果没有控制好右侧节点的链表指向,可能会造成死循环的问题。
解决问题的关键,当遍历到最左边节点的右子树为空的状态或者右子树已经处理过,需要用pre记录这个节点,表示该节点以及它的子树已经完全处理好了,避免造成栈与链表的循环访问即可。
/**
* 后序遍历迭代
*
* @param root
*/
public List<Integer> postOrder2(BTNode root){
Stack<BTNode> stack=new Stack<>();
List<Integer> res = new ArrayList<Integer>();
if(root==null) return res;
BTNode cur=root;
//当遍历到右节点为空的状态时,需要记录他的pre节点
BTNode pre=null;
while (!stack.empty()||cur!=null){
// cur不为null时入栈,向left方向推进直到粗人为空
while (cur!=null){
stack.push(cur);
cur=cur.left;
}
//cur为空,看看该节点有无右子树或者已经处理过右子树
BTNode top=stack.peek();
if(top.right==null||top.right==pre){
//1.top.right==null右树为空,说明为叶子节点,直接添加top.val
//2.top.right==pre右树已经处理过了,左树为空,右树处理过,直接添加top.val就可以了
stack.pop();
res.add(top.val);
//用pre记录这个节点,表示该节点以及它的子树已经完全处理好了
pre=top;
}else {
cur=cur.right;
}
}
return res;
}
还有一种比较好理解的解法:
先序遍历是中左右,后序遍历是左右中,那么我们只需要调整一下解法二先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了
代码:
public List<Integer> postOrder3(BTNode root){
Stack<BTNode> stack=new Stack<>();
List<Integer> res = new ArrayList<Integer>();
if(root==null) return res;
BTNode cur=root;
stack.push(cur);
while (!stack.empty()){
BTNode top=stack.pop();
res.add(top.val);
if(top.left!=null)stack.push(top.left);
if(top.right!=null)stack.push(top.right);
}
Collections.reverse(res);
return res;
}
Morris算法
有一种巧妙的方法可以在线性时间内,只占用常数空间来实现前、中、后序遍历。这种方法由 J. H. Morris 在 1979
年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出,因此被称为 Morris
遍历。
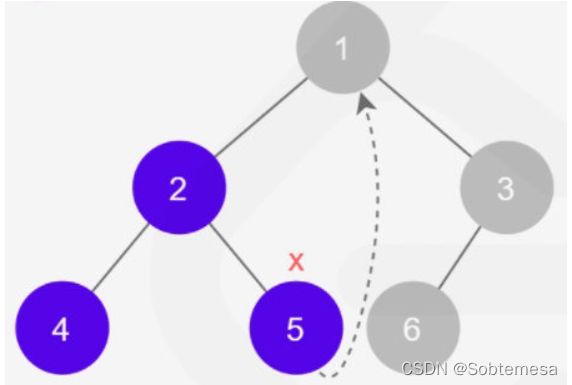
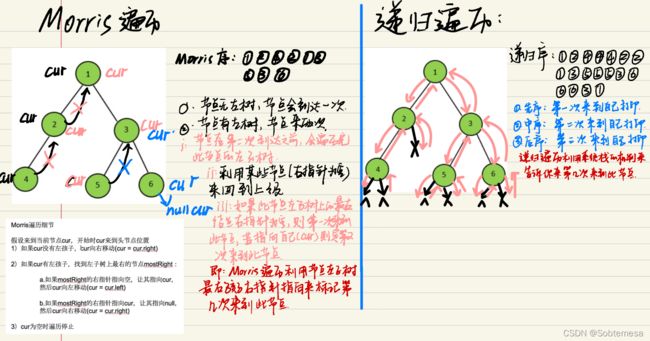
二叉树的前中后序遍历均涉及到从根出发,向叶子方向推进后再返回的过程。无论是递归方法还是显式地使用栈的迭代方法,能够返回的关键均在于栈。思考如何在不使用栈的情况下实现二叉树遍历时的返回动作。以下图的中序遍历为例,在完成[4, 2, 5]的遍历之后要遍历1(将1加入到结果中),如果在完成5的遍历后能够通过5的指针信息返回到1,就有可能在不使用栈的情况下完成二叉树的遍历。实际上这就是线索二叉树(Threaded Binary Tree)的思想,而Morris遍历算法正是这种思想的具体应用。
Morris遍历细节:
假设来到当前节点cur,开始时cur来到头节点的位置
1)如果cur没有左孩子,cur向右移动(cur=cur.right)
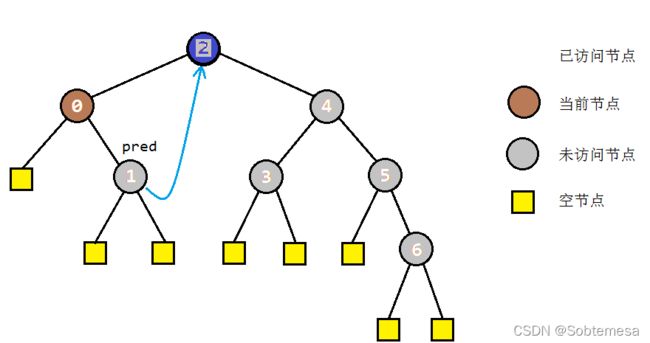
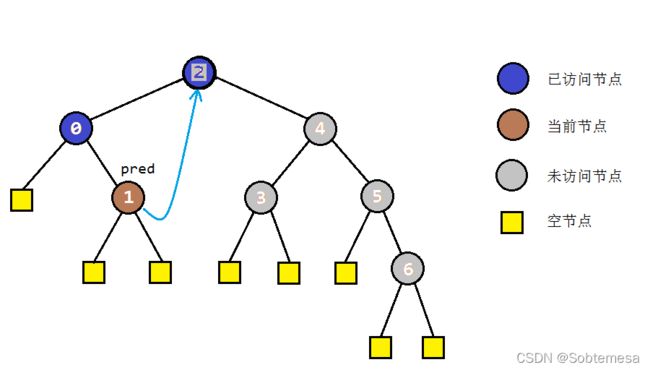
2)如果cur有左孩子,找到左子树上最右的节点pred,即中序遍历下当前节点的前驱节点
a:如果pred.right==null,置prev=cur,然后cur向左移动(cur=cur.right)
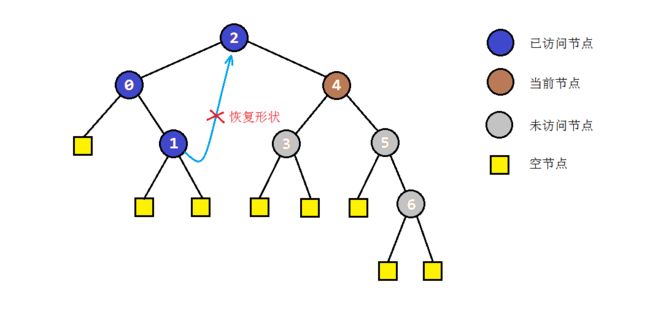
b:如果pred.right==cur,让其指向null,恢复树形,然后cur向右移动(cur=cur.right)
3)cur==null时遍历结束
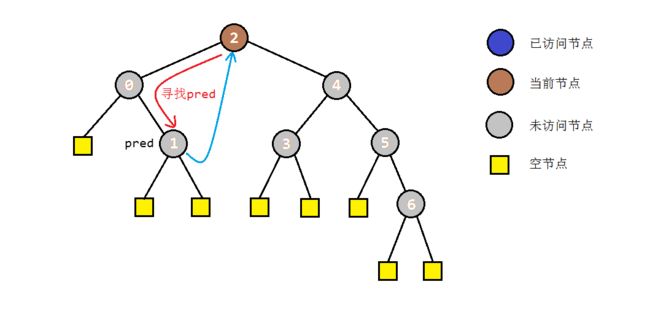
图示:
cur依次遍历的序列叫做Morris序,上图的Morris序列为:2 0 1 2 4 3 4 5 6
1)如果节点没有左树,遍历时只到达一次。
2)如果节点有左树,遍历时到达两次。
3)节点在第二次到达之前会遍历完此节点的左树。
4)Morris遍历用节点左子树最右节点右指针的指向来标记第几次来到此节点。
a:如果最右节点右指针指向为空,则为第一次来到此节点。
b:如果最右节点右指针指向为此节点,则为第二次来到此节点。
判断前中后序:
1)前序遍历:第一次来到此节点,打印。则为:2 0 1 4 3 5 6
代码:
/**
* 前序遍历morris
* * @param root
* @return
*/
public void preOrder4(BTNode root){
BTNode pred=null;
BTNode cur=root;
if(root==null) return;
while (cur!=null){
pred=cur.left;
//cur有左子树,能来到此节点二次
if(pred!=null){
//寻找此节点的前驱节点,即其左子树上的最右节点pred
while (pred.right!=null&&pred.right!=cur){
pred=pred.right;
}
//第一次来到此节点
if(pred.right==null){
System.out.print(cur.val+"->");
pred.right=cur;
cur=cur.left;
continue;
}
//第二次来到此节点,说明此节点的左子树都已经遍历过了
else {
pred.right=null;
cur=cur.right;
}
}
//cur没有左子树,只来到此节点一次
else {
System.out.print(cur.val+"->");
cur=cur.right;
}
}
System.out.println();
}
2)中序遍历:0 1 2 3 4 5 6
a:如果节点有左树,遍历时到达两次,第二次来到此节点时打印。
b: 如果节点没有左树,遍历时只到达一次,第一次来到此节点时打印。
代码:
/**
* 中序遍历morris
* @param root
*/
public void inOrder4(BTNode root){
BTNode pred=null;
BTNode cur=root;
if(root==null) return;
while (cur!=null){
pred=cur.left;
//cur有左子树,能来到此节点二次
if(pred!=null){
//寻找此节点的前驱节点,即其左子树上的最右节点pred
while (pred.right!=null&&pred.right!=cur){
pred=pred.right;
}
//第一次来到此节点
if(pred.right==null){
pred.right=cur;
cur=cur.left;
continue;
}
//第二次来到此节点,说明此节点的左子树都已经遍历过了
else {
System.out.print(cur.val+"->");
pred.right=null;
cur=cur.right;
}
}
//cur没有左子树,只来到此节点一次
else {
System.out.print(cur.val+"->");
cur=cur.right;
}
}
System.out.println();
}
3)后序遍历:1 0 3 6 5 4 2
第一步:找能遍历到两次的节点,逆序打印该节点左树右边界。
第二步:逆序打印整棵树的右边界。
/**
* 后序遍历morris
* @param root
*/
public void postOrder4(BTNode root){
BTNode pred=null;
BTNode cur=root;
if(root==null) return;
while (cur!=null){
pred=cur.left;
//cur有左子树,能来到此节点二次
if(pred!=null){
//寻找此节点的前驱节点,即其左子树上的最右节点pred
while (pred.right!=null&&pred.right!=cur){
pred=pred.right;
}
//第一次来到此节点
if(pred.right==null){
pred.right=cur;
cur=cur.left;
continue;
}
//第二次来到此节点,说明此节点的左子树都已经遍历过了
else {
pred.right=null;
print(cur.left);
cur=cur.right;
}
}
//cur没有左子树,只来到此节点一次
else {
cur=cur.right;
}
}
print(root);
}
//逆序打印出此节点左子树的右边界,打印完要逆置回来
public void print(BTNode head){
BTNode tail=reverseEdge(head);
BTNode cur=tail;
while (cur!=null){
System.out.print(cur.val+"->");
cur=cur.right;
}
reverseEdge(tail);
}
//类似于单链表的逆置
public BTNode reverseEdge(BTNode head){
BTNode pre=null;
BTNode next=null;
while (head!=null){
next=head.right;
head.right=pre;
pre=head;
head=next;
}
return pre;
}