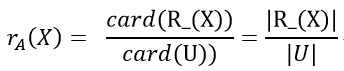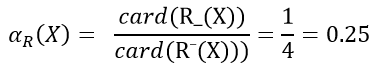粗糙集理论
粗糙集理论
1 粗糙集的特点与应用领域
性质: 粗糙集理论是一种处理不精确、不确定与不完全数据的新的数学方法。
应用领域 : 机器学习与知识发现、数据挖掘、决策支持与分析、专家系统、归纳推理、模式识别等方面的广泛应用，现已成为一个热门的研究领域。RS理论主要兴趣在于它恰好反映了人们用Rough集方法处理不分明问题的常规性,即以不完全信息或知识去处理一些不分明现象的能力。或依据观察，度量到的某些不确定的结果而进行分类数据的能力。
粗糙集理论的优点及局限性主要优点
优点: 除数据集之外，无需任何先验知识(或信息)对不确定性的描述与处理相对客观。
[说明] : Bayes理论、模糊集理论、证据理论等都需要先验知识，具有很大的主观性。
1.1 不确定性理论
自然界和人类的社会活动的各种现象:确定性现象和不确定性现象。确定性现象:在一定条件下必然会出现的现象。
1.1.1 不确定性的分类
随机性 :因为事物的因果关系不确定，从而导致事件发生的结果不确定性。用概率来度量。概率表示事件发生可能性的大小。概率论的运用是从随机性中去把握广义的因果律─概率规律。
模糊性: 因为事件在质上没有明确的含义，在量上没有明确的界限，导致事件呈现"亦此亦彼"的性态，是事物类属的不确定性，用隶属度来度量。隶属度表示事物多大程度属于某个分类。模糊集合论的运用从模糊性中去确立广义的排中律─隶属规律。
粗糙性 :因为描述事件的知识(或信息)不充分、不完全，导致事件间的不可分辨性。粗糙集把那些不可分辨的事件都归属一个边界域。因此，粗糙集中的不确定性是基于一种边界的概念，当边界域为一空集时，则问题变为确定性的。
1.1.2 经典集合、模糊集合、粗糙集的关系.
经典集合认为一个集合完全有其元素所决定，一个元素要么属于这个集合，要么不属于这个集合。其隶属函数μ_x(x)∈{0, 1}是二值逻辑。
模糊集合认为事物具有中介过渡性质，而非突然改变，集合中每一个元素的隶属函数μ_x(x)∈[0, 1]，即在闭区间[0, 1]可以任意取值，隶属函数可以是连续光滑的,因此模糊集合对不确定信息的刻划是精细而充分的。但隶属函数不可计算，凭人的主观经验给定。
粗糙集合把用于分类的知识引入集合。一个元素x是否属于集合X，需要根据现有知识来判定，可分为三个情况:
① x肯定不属于X;
② x肯定属于X;
③ x可能属于也可能不属于X。
到达属于哪种情况依赖于我们所掌握的关于论域的知识。粗糙集的隶属函数为阶梯状，对不确定性信息的描述是粗糙的，但粗糙隶属函数是可计算的。粗糙集主要用于对信息系统进行约简和分类。
1.2 粗糙集的基本概念
1.2.1 知识与分类
在粗糙集理论中，知识被认为是一种分类能力，人们的行为基本是分辨现实的或抽象的对象的能力。
假定我们起初对论域内的对象(或称元素、样本、个体)已具有必要的信息或知识，通过这些知识能够将其划分到不同的类别。若我们对两个对象具有相同的信息，则它们是不可区分的，即根据已有的信息不能将其划分开。
粗糙集理论的核心是等价关系，通常用等价关系替代分类， 根据等价关系划分样本集合为等价类。集合上的等价关系和集合上的划分是一一对应，相互唯一决定的。 从数学意义上讲，集合上的等价关系和集合的划分是等价的概念，即划分就是分类。
基本思想: 从知识库的观点看，每个等价类被称为一个概念，即一条知识(规则)。即每个等价类唯一地表示了 一个概念，属于一个等价类的不同对象对该概念是不可区分的。
1.2.2 知识表达系统
1.2.3 不可分辨关系
在粗糙集中，论域U中的对象可用多种信息(知识)来描述。当两个不同的对象由相同的属性来描述时，这两个对象在该系统中被归于同一类，它们的关系称之为不可分辨关系。即对于任一属性子集BR,如果对象, U， rB，当且仅当f( : r)=f(: r)时，和是不可分辨的，简记为LND(B)。不可分辨关系称为等价关系。
例如: 只用黑白两种颜色把空间中的一些物体划分成两类:{黑色物体}、{白色物体}，那么同为黑色的物体就是不可分辨的，因为描述它们特征属性的信息是相同的，都是黑色。如果引入方、圆的属性，可将物体进一步划分为4类: {黑色 方物体}、{黑色圆物体}、{白色方物体}、{白色圆物体}。这时，如果有两个同为黑色方物体，则它们还是不可分辨的。不可分辨关系这一概念在RS中十分重要，它反映了我们对世界观察的不精确性。
另一方面，不可分辨关系反映了论域知识的颗粒性。知识库中的知识越多，知识的颗粒度就越小，随着新知识不断加入到知识库中，粒度会不断减小，直至将每个对象区分开来。但知识库中的知识粒度越小，则导致信息量增大，存储知识库的费用越高。
1.2.4 基本集合
由论域中相互不可分辨的对象组成的集合称之为基本集合，它是组成论域知识的颗粒。
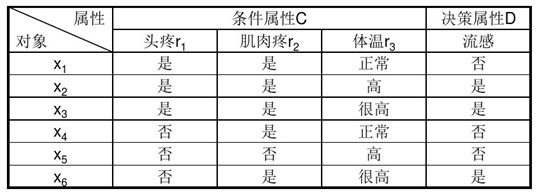
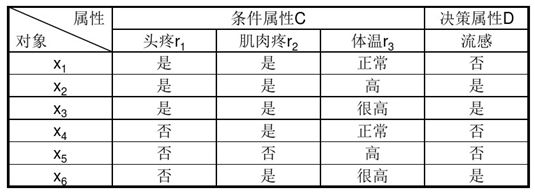例如: 考虑条件属性:头疼和肌肉疼。对于X1, X2, X3这三个对象是不可分辨的。X4, X6在这
两个属性上也是不可分辨的。由此构成不可分辨集{ X1, X2, X3}，{ X4, X6}，{ X5}被称为基本集合。
设论域U为有限集，R是U的等价关系簇，则K= {U, R}称为知识库，知识库的知识粒度由不可分辨关系Ind®的等价类反映。
1.2.5 下近似集和上近似集
U/R 的含义：
设U是一个论域，R是U上的等价关系，U/R表示U上由R导出的所有等价类。
等价类：
等价关系划分样本集合为等价类。
[x]R的含义：
[x]R 表示包含元素x ∈U的R等价类。
下近似集
根据现有知识R，判断U中所有肯定属于集合X的对象所组成的集合，即
R_ (x)={x ∈U, [x]R }
其中，[x]R表示等价关系R下包含元素x的等价类。
上近似集
根据现有知识R，判断U中一定属于和可能属于集合X的对象所组成的集合，即
R¯(x)={x ∈U, [x]R ∩X ≠ф}
其中，[x]R 表示等价关系R下包含元素x的等价类。
给定知识表达系统S={U,R, V, f}， 对于每个样本子集X U和等价关系R，所有包含于X的基本集的并(逻辑和)为R_ (X);所有与X的交(逻辑积)不为空集的基本集的并为R_ (X)。
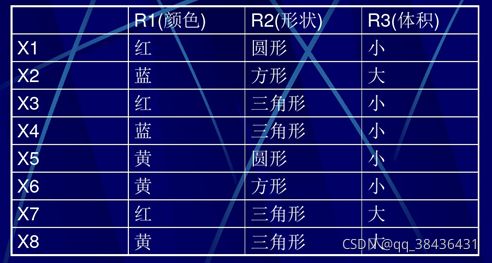
例** 1** 给定玩具积木的集 合U ={x1,x2…x8},并假设这些积木有不同的颜色(红、黄、蓝)，形状(方、圆、三角)和体积(大、小)。积木的集合U可按颜色、形状、体积分类。R1颜色关系，R2形状关系，R3体积。则
U/R1 = {{x1, x3, x7}, {x2, x4}, {x5, x6, x8}}
U/R2 = {{x1, x5}, {x2, x6}, {x3, x4, x7, x8}}
U/R3 = {{x2, x7, x8}, {x1, x3, x4, x5, x6}}
取 X = {x2, x4, x7} 那么
R1_(X) = {x2, x4}
R1¯(X) = {x2, x4} {x1, x3, x7} = {x2, x4, x1, x3, x7}
R2_(X) = ф
R2¯(X) = {x2, x6, x3, x4, x7, x8}
R3_(X) = ф
正域：
下近似R_(X)也称为X关于近似空间A的正域，记为POSR (X)。解释为:由那些根据现有知识判断出肯定属于X的对象所组成的最大集合。
负域：
U - R¯(X)称作X关于A的负域，记为NEGR(X)。解释为:由那些根据现有知识判断肯定不属于X的对象所组成的集合。
上近似
R¯(X)可以解释为:由那些根据现有知识判断出可能属于X的对象所组成的最小集合。
边界域：
R¯(X) - R_(X) 称作X的边界域记为BNDR(X)。解释为:由那些根据现有知识判断出可能属于X但不能完全肯定是否一定属于X的对象所组成的集合。
X是可定义的 R¯(X) = R_(X)
X是不可定义的R¯(X) ≠ R_(X)
此时称X在近似空间A中是粗糙集。
1.2.6 粗糙度(近似精确度)
近似精确度
对于知识R (即属性子集)，样本子集X的不确定程度可以用粗糙度来表示为
亦称近似精确度，式中 Card 表示集合的基数(集合中元素的个数)。0≤≤1， 如果=1，则称集合X相对于R是确定的，如果<1则称集合X相对于R是粗糙的，可认为是在等价关系R下逼近集合X的精度。
近似质量
X关于A的近似质量:
近似质量反映了知识X中肯定在知识库中的部分在现有知识中的百分比。
粗糙性测度
X 关于 A 的粗糙性测度
≤ρ_A≤1，粗糙性测度反映了知识的不完全程度。
例1:以医疗信息表为例，对于属性子集R= {头疼,肌肉疼}={r1,r2},计算样本子集X={x1, x2, x5}的上近似集、下近似集、正域、边界域。
解：
①计算论域U的所有R基本集:
U | IND® = {{x1, x2, x3}, {x4, x6}, {x5}}
令R1 = {x1, x2, x3}, R2 = {x4, x6}, R3 = {x5}
② 确定样本子集X与基本集的关系
X ∩ R1 = {x1, x2} ≠ ф X ∩ R2 = ф X ∩ R3= {x5} ≠ф
③ 计算R_ (X)、 R¯(X)、POS(X)、 BUN(X):
R_(X) = R3 = {x5}
R¯(X) = R1 U R3={x1, x2, x3, x5}
POS(X)=R_(X)={x5}
BND(X)=R¯(X) - R_(X)={x1, x2, x3}
④ 计算近似精确度:
2 粗糙集的基本思想
2.1 RS的基本思想
RS认为知识就是将论域中的对象进行分类的能力。对对象的认知程度取决于所拥有的知识的多少，知识越多，则分类能力越强。知识越少，则对象间的区分越模糊。
在没有掌握所有关于对象域的知识的情况下，为了刻画模糊性，RS使用了一对称为下近似与上近似的精确概念来表示每个不精确概念，即使用上边界、下边界对逼近来描述对象域上的集合。下近似和上近似的差是一个边界集合，它包含了所有不能确切判定是否属于给定类的对象。这种处理可以定义近似的精确度，能够很好的近似分类，得到可以接受质量的分类。
在RS中，论域中的对象可用多种知识来描述(通常描述为属性)。当两个不同的对象由相同的属性来描述时，这两个对象在系统中被归于同一类，它们的关系称之为不可分辨关系或等价关系。不可分辨关系是RS理论的基石，它反映了论域知识的颗粒性。
影响分类能力的属性很多，不同的属性重要程度不同，其中某些属性起决定性作用;属性的取值不同对分类能力也会产生影响。RS理论提出知识的约简方法、在保留基本知识、对对象的分类能力不变的基础上，消除重复、冗余属性和属性值,实现了对知识的压缩和再提炼。
2.2 粗糙集的基本特点
RS的基本特点RS的基本方法是使用等价关系将集合中的元素(对象)进行分类，生成集合的某种划分，与等价关系相对应。根据等价关系的理论，同一分类(等价类)内的元素是不可分辨的，对信息的处理可以在等价类的粒度上进行，由此可以达到对信息进行简化的目的。
RS是一种软计算方法，传统的知识处理是一种硬计算方法，使用精确、固定和不变的算法来表达和求解问题。而软计算方法则允许利用不精确性、不确定性和部分真实性以得到易于处理、鲁棒性强和低成本的解决方案。
RS仅仅从数据本身进行分析，无需提供所要分析的样本数据以外的任何先验知识或附加信息，不要预先给予主观评价，如统计学中要假定概论分布，模糊集中要.给定隶属度，证据理论中要赋予似然值等。
RS能分析各种数据，包括确定性和非确定性的;不精确的和不完整的以及拥有众多变量的数据，并对数据进行简化，从而发现知识、推理决策规则，不仅是一种决策分析方法，而且是一种系统建模方法。
RS与其他不确定方法一样，它们都是处理含糊性和不确定性问题的数学工具。但它们又有不同之处:主观Bayes中，不确定性看成概率; D/S证据理论中，不确定性是可信度;模糊集合理论中，不确定性是集合的隶属度; RS理论中，不确定性是上、下近似集之差，有确定的数学公式来描述。
由于RS理论本身未包含处理不精确或不确定原始数据的机制，在实际应用中，RS方法常常需要与其他方法结合起来使用，互为补充。
2.3 知识的约简
设U为所讨论对象的非空有限集论域，R为非空的属性有限集，则称二元有序组K={U, R}为一个知识库，亦称近似空间。
在知识库中可能含有冗余的知识，知识约简是研究知识库中哪些知识是必要的，以及在保持分类能力不变的前提下，删除冗余的知识。特别是，当信息系统中的数据是随机采集的其冗余性更为普遍。知识约简是粗糙集理论的核心内容之一，在信息系统分析与数据挖掘等领域具有重要的应用意义。
2.3.1 一般约简
在粗糙集理论中，约简与核是两个最重要的基本概念。设R是一个等价关系族，且r ∈R,若有
Ind( R )=Ind( R，{r} )
则称r在等价关系族R中是可省略的，否则r为R中不可省略的。
若族R中每一个r都是不可省略的，则称族R为独立的。在用属性集R表达系统的知识时，R为独立的意味着属性集中的属性是必不可少的。它独立地构成一组表达系统分类知识的特征。
2.3.2 等价关系族的核
定义:设QP，若Q是独立的，且Ind( Q )=Ind ( P ),则称Q是等价关系族P的一个约简,记为Red§。在P中所有不可省略关系的集合交集称为等价关系族P的核，记为Core §。
知识约简与核的关系是:
约简集Red§的交集等与P的核，即：Core§=∩Red§
方面核是所有约简的计算基础;另一方面，核是知识库中最重要的部分，是进行知识约简时不能删除的知识。
2.3.3 相对约简
在实际应用中，一个分类相对于另一个分类的关系非常重要。在粗糙集中相对约简的概念，即条件属性相对决策属性的约简。设P和Q为论域U上的等价关系，Q的P正域记为POSp(Q),即
POSp (Q)=∪P_ (X)
Q的P正域是论域U中的所有那些使用分类U/P所表达的知识，能够正确地划入到U/Q的等价类之中的对象给出的集合。
一个集合X相对于一个等价关系P的正区域就是这个集合的下近似P_ (X);而一个等价关系Q相对于另一个等价关系P的正区域的概念是解决分类Q的等价类(一般视为决策类)之中的那些对象可由分类P的等价类(一般视为条件类)来分类的问题。
设P和Q为论域U上的等价关系，rP。若
则称r为P中Q可省的，否则称r为P中Q不可省的。上式可记为
当P中的每一个r都是Q不可省的，则称P是相对于Q独立的，否则就称为是依赖的。
当(P- r)为的Q独立子族，且,则族(P-r)称为P的Q相对约简，记为。它是用属性P表达属性Q必不可少的属性集，如果从分类的观点看，就是用一种分类关系表达另一种分类关系必不可少的关系集合。
2.3.4 知识的依赖性
知识库中的知识并不是同等重要的，有些知识可以由其他知识导出。知识的依赖性可以形式化地描述为:
令K={U,R}为一知识库，且P， QR，则
①当Ind§Ind(Q)，知识Q依赖于知识P，记作PQ;
②当PQ且QP，知识P和Q是等价的;
③当不存在PQ且不存在QP，P、Q是独立的。
如果知识Q依赖于P，则有下面的结论:
- LND§ LND (Q);
② LND (P∪Q) LND §;
③ (Q) =U;
④若任一x ∈U/Q， 则P_ (X)=X。
2.3.5 分辨矩阵
为了简化核、约简与其它概念的计算，Skowron在1991年提出了分辨矩阵的概念。设S=<U, A, V, f>, U={,…,}, BA的分辨矩阵M(B)定义为:
是区别对象和的所有属性集。
B核是M(B)中全部含有单个元素的条目的并集即:
若存在一个B的最小子集使得对于M(B)中的任意非空条目有则是B的约简。
相对约简与相对核
设C、D是A的两个非空子集，C为条件属性，D为决策属性，则C的分辨矩阵定义为:
其中
的意义:表示两个对象有且只有一个存在于中，或者若二者均存在于中，但二者对属性集D不等价。如果D诱导的划分可由知识C定义即所有对象均属于则可简化为
C的D核:是中所有含单个元素的条目的并集。
C的D约简:若存在一个C的最小子集，使得对于中的任意非空条目有,则是C的D约简。
按定义，C的D分辨矩阵为主对角线为空集的对称阵:
非空条目有则是B的约简。
相对约简与相对核
设C、D是A的两个非空子集，C为条件属性，D为决策属性，则C的分辨矩阵定义为:
其中
的意义:表示两个对象有且只有一个存在于中，或者若二者均存在于中，但二者对属性集D不等价。如果D诱导的划分可由知识C定义即所有对象均属于则可简化为
C的D核:是中所有含单个元素的条目的并集。
C的D约简:若存在一个C的最小子集，使得对于中的任意非空条目有,则是C的D约简。
按定义，C的D分辨矩阵为主对角线为空集的对称阵:
