Eigen——C++矩阵运算库

1.Eigen是什么？

Eigen是一个基于C++模板的开源库，支持线性代数，矩阵和矢量运算，数值分析及其相关的算法。

2.下载配置

• 官网：Eigen官网，下载解压缩可以重命名为eigen3。官网介绍使用Eigen，只需要下载它的源码，事实上，Eigen子目录中的头文件是使用Eigen编译程序所需的惟一文件。所有平台的头文件都是相同的。不需要使用CMake或安装任何东西。
  

• 写一个简单的项目，包含头文件。注：Eigen使用源代码方式提供用户使用，在使用时只需要包含Eigen头文件即可使用。

  #include 
  #include 
  using Eigen::MatrixXd;
  int main()
  {
    MatrixXd m(2,2); //MatrixXd类型，代表一个任意大小的矩阵
    m(0,0) = 3;
    m(1,0) = 2.5;
    m(0,1) = -1;
    m(1,1) = m(1,0) + m(0,1);
    std::cout << m << std::endl;
  }
  

• 在项目——属性——C/C++——常规——附加包含目录添加该库位置就好了，这个操作是指包含头文件，没有链接到的库。在编译上述程序时，只需要一个操作，即让编译器能够找到Eigen的头文件。放置Eigen源代码的目录必须位于包含路径中。

官网安装和配置说明（包含使用的简单介绍）：Getting started
图文详细：vs2013配置Eigen库

3.使用

官网的快速参考指南：Quick reference guide

3.1 模块和头文件

Eigen库被分为一个核心模块和几个别的模块，每个模块有一个对应的头文件，使用该模块需要包含对应头文件。还提供了Dense和Eigen头文件方便同时使用多个模块。

模型	头文件	说明
Core	#include	包含Matrix和Array类，基础的线性代数运算和数组操作。
Geometry	#include	包括平移、缩放、2D\3D旋转变换、四元数、轴旋转变换
LU	#include	包含求逆，行列式，LU分解
Cholesky	#include	包含LLT和LDLT Cholesky分解
Householder	#include	householder变换，此模块由几个线性代数模块使用
SVD	#include	奇异值分解
QR	#include	QR分解
Eigenvalues	#include	特征值、特征向量
Sparse	#include	稀疏矩阵存储及相关的基本线性代数
*	#include	包含Dense和Sparse头文件（Eigen全部库）

3.2 每个具体使用，下面有相对官网的中文博客

Eigen库使用指南
Eigen: C++开源矩阵计算工具——Eigen的简单用法
Eigen矩阵库使用说明
*** Eigen和Matlab对应说明

3.3 下面只记录我要用的，一边用一边记

1、Matrix（矩阵） 和 Array（数组）类 ：分别表示数学矩阵和向量
所有的矩阵和向量都是Matrix模板类的对象，Matrix有 6个模板参数，主要用的前三个，其他默认的。

typedef Matrix<Scalar, RowsAtCompileTime, ColsAtCompileTime, Options> MyMatrixType;
typedef Array<Scalar, RowsAtCompileTime, ColsAtCompileTime, Options> MyArrayType;
// Scalar:数据的标量类型（e.g. float,double,bool,int,etc）
// RowsAtCompileTime:矩阵行数 rows
// ColsAtCompileTime:矩阵列数 cols
// Option:选项可以是ColMajor或RowMajor，默认是ColMajor

上面的模板里的参数可以随意组合，然后矩阵的行列数可以是固定的也可以是动态的，但是这里的动态，我感觉并不是链表什么的那样，只是在构造那个对象的时候不指定行列数，程序执行的时候还是要给行列数。我用改变大小之前矩阵里面的数会没。还有点乱，后面再看吧。动态可以重新改变矩阵大小（值得注意 resize（）），且在使用 “=”的时候，若和等号右边的大小不一样，会自动变成等号右边的大小。

Matrix<double, 6, Dynamic>                  // Dynamic number of columns (heap allocation)
Matrix<double, Dynamic, 2>                  // Dynamic number of rows (heap allocation)
Matrix<double, Dynamic, Dynamic, RowMajor>  // Fully dynamic, row major (heap allocation)
Matrix<double, 13, 3>                       // Fully fixed (usually allocated on stack)

这里面给了一些typedef，所以一些使用的时候可以用简化的类型名。

//动态大小
typedef Matrix<double,Dynamic,Dynamic> MatrixXd;
typedef Matrix<float, Dynamic, 1> VectorXf; //默认都是列向量
// 列向量
typedef Matrix<double, 3, 1> Vector3d;
// 行向量
typedef Matrix<int, 1, 3> RowVector3i;

typedef Array<double,Dynamic,Dynamic> ArrayXXd;
typedef Array<double,Dynamic,1> ArrayXd;
typedef Array<int,1,Dynamic> RowArrayXi;
typedef Array<float,3,3> Array33f;
typedef Array<double,4,1> Array4f;

2、基础矩阵操作
1）构造

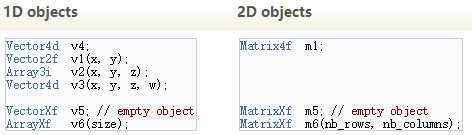
2）初始化，给矩阵元素赋值，这里有两种方式：

• 一种是"<<"操作符，用该操作符一个一个的赋值（注意顺序是从左到右，从上到下），或者一块一块的赋值。另外还有一些特殊矩阵（零矩阵，单位矩阵，常数矩阵）。

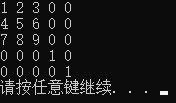
   // 挨个赋值
  Matrix3f  m1;   
  m1 << 1, 2, 3,
  4, 5, 6,
  7, 8, 9;
  cout << m1 << endl;
  // 分块儿赋值，这对两个矩阵合并有用
  int rows = 5, cols = 5;
  MatrixXf m(rows, cols);
  m << (Matrix3f() << 1, 2, 3, 4, 5, 6, 7, 8, 9).finished(),
  MatrixXf::Zero(3, cols - 3),
  MatrixXf::Zero(rows - 3, 3),
  MatrixXf::Identity(rows - 3, cols - 3); //   Zero()、Identity() 分别是0矩阵和单位矩阵。
  cout << m << endl;
  

  输出 ：

  • 一种是按下标赋值

    int rows = 5, cols = 5;
    MatrixXf m(rows,cols);
    for (int i = 0; i < rows; i++)
    {
    	for (int j = 0; j < cols; j++)
    	{			
    		m(i, j) = 2;
    	}
    }
    cout << m << endl;
    

    输出：

• 特殊矩阵：

  Constant(rows,cols,value); //常量矩阵
  Random();//随机
  Zeor();//0
  Identity();//单位
  

3）矩阵大小获得和改变
矩阵的当前行、列、元素个数可以通过 rows()，cols()，size()来检索，这些方法分别返回行数、列数和系数数。调整动态数组的方法是通过 resize()方法。

值得注意的是这个 resize()函数，只能修改动态矩阵的大小。且 resize() 函数会析构掉原来的数据，因此调用resize() 函数之后将不能保证元素的值不改变。 使用 conservativeResize()来不改变矩阵本来内容。可以在这里搜一下这个函数具体看下用法

conservativeResize(Index rows,Index cols)//调整矩阵的大小到第x行，而保持原来的值不变。
conservativeResize(NoChange_t, Index);//只改变行数
conservativeResize(Index, NoChange_t);//只改变列数

4）运算

	MatrixXf m1;
	m1 = MatrixXf::Random(3, 3);
	cout << m1 << endl;
	cout << m1.transpose() << endl; //转置
	cout << m1.conjugate() << endl; //共轭
	cout << m1.adjoint() << endl; //共轭转置（伴随矩阵）


	MatrixXd m2(2, 2);
	m2 << 1, 2, 3, 4;
	cout << m2 << endl;
	cout << m2.sum() << endl;//所有元素求和
	cout << m2.prod() << endl;//所有元素乘积
	cout << m2.mean() << endl;//所有元素求平均
	cout << m2.minCoeff() << endl;//所有元素中最小值
	cout << m2.maxCoeff() << endl;//所有元素中最大值
	cout << m2.trace() << endl;//迹

	Vector3d v1(1, 2, 3);
	Vector3d v2(4, 5, 6);
	Vector3d v;
	double dot_value, norm_value;
	dot_value = v1.dot(v2);//点乘，得到的是标量
	v = v1.cross(v2);//叉乘，得到的是向量
	cout << dot_value << endl;
	cout << v << endl;
	norm_value = v1.norm();//求模
	cout << norm_value << endl;
	
	system("pause");

5）块操作
官网：Block operactions
块是矩阵中的矩形的子块。
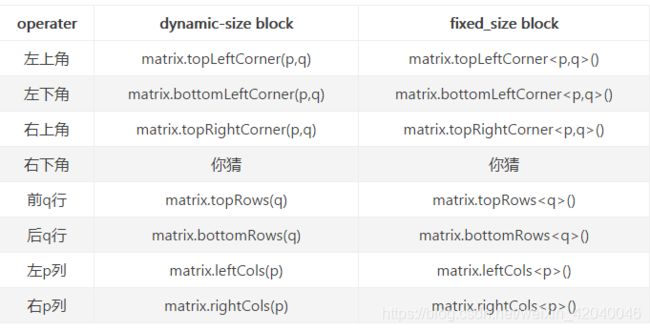
矩阵Matrix 的块操作：

//矩阵的块操作：
//表示返回从矩阵的（i，j）开始，每行取P个元素，每列取q个元素，原矩阵不变
matrix.block(i,j,p,q);
//原矩阵中第(i, j)开始，获取一个p行q列的子矩阵，返回该子矩阵组成的临时 矩阵对象，原矩阵的元素不变
matrix.block<p,q>(i,j);

//获取矩阵中的某行某列
matrix.row(i);// 矩阵第i行
matrix.col(j);//矩阵第j列

Matrix矩阵角相关操作:

向量Array 的块操作，其实光用矩阵也行，不用定义向量对象

vector.head(n);//获取向量的前n个元素
vector.tail(n);//获取向量尾部的n个元素
vector.segment(i,n);//获取从向量的第i个元素开始的n个元素