【数据结构初阶】新学期带你领跑二叉树，二叉树的迭代遍历，递归遍历详解，建议收藏

---

前言

首先我们这里所讲述的二叉树是最为常见的，本章主要带大家了解这种二叉树，并且学会它常见的遍历方式（递归，迭代），由于普通的二叉树没有插入删除的意义，到了AVL，红黑树这种平衡二叉搜索树才有插入删除的意义，所以我们在本章节主要是带大家先简要理解这种结构，对于二叉树有一个初步的认识。

---

一、二叉树的结构介绍

// 对int typedef 是因为二叉树的节点可以存放任意的值，这里是为了方便后续有需要方便调整
typedef int BTDataType;
// 二叉树
typedef struct BinaryTreeNode
{
	//二叉树的每一个节点都有一个值
	BTDataType val;
	//二叉树的每一个节点都有指向左孩子（右孩子）的指针
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

这就是一个常见的二叉树

二、二叉树的遍历（递归）（易）

1.前序遍历

对于一棵树，树的本身性质让他非常适合递归，当我们想要递归一颗树的时候，我们可以访问它的根，左子树，右子树，注意是左子树不是左孩子，左子树又可以分成根，左子树，右子树

前序遍历也是标准的深度优先搜索模式：遍历当前节点，再往深处走，走到底就回来尝试新的方法❗️❗️❗️❗️

❗️❗️❗️接下来我们尝试创建这样上图所示的树

// 创建节点并进行初始化
BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->left = NULL;
	newnode->right = NULL;
	newnode->val = x;
	return newnode;
}
//手动创建一棵树
BTNode* CreateTree()
{
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');
	BTNode* nodeG = BuyNode('G');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeB->right = nodeE;
	nodeC->left = nodeF;
	nodeC->right = nodeG;
	nodeD->left = NULL;
	nodeD->right = NULL;
	nodeE->left = NULL;
	nodeE->right = NULL;
	nodeF->left = NULL;
	nodeF->right = NULL;
	nodeG->left = NULL;
	nodeG->right = NULL;
	return nodeA;
}

❗️❗️❗️我们可以先预测结果，如果将NULL也打印出来的话，上面得到的前序遍历的结果应该是
A B D NULL NULL E NULL NULL C F NULL NULL G NULL NULL

void PreOrder(BTNode* root)
{
	//我们这里用打印的方式表示遍历这个节点的值
	if (root == NULL)
	{
		//如果这棵树本身是空，或者递归到空的位置我们打印NULL
		//再返回上一层
		printf("NULL ");
		return;
	}
	//访问当前节点
	printf("%c ", root->val);
	//访问当前节点的左子树
	PreOrder(root->left);
	//访问当前节点的右子树
	PreOrder(root->right);
}

看不懂的同学可以按照上面来那张图片想一想

---

2.中序遍历

❗️❗️❗️
对于中序遍历我们先走左子树，根，右子树
例子：ABCDEFG（层序）
我们也可以预测中序遍历的结果：
NULL D NULL B NULL E NULL A NULL F NULL C NULL G NULL

void Inorder(BTNode* root)
{
	if (root ==  NULL)
	{
		printf("NULL ");
		return;
	}
	//访问左子树
	Inorder(root->left);
	//根
	printf("%c ", root->val);
	//右子树
	Inorder(root->right);
}

---

3.后序遍历

❗️❗️❗️
后序遍历：左右根
例子：ABCDEFG（层序）
我们也可以预测中序遍历的结果：
NULL NULL D NULL NULL E B NULL NULL F NULL NULL G C A

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	//左子树
	PostOrder(root->left);
	//右子树
	PostOrder(root->right);
	//根
	printf("%c ", root->val);
}

其实到这里大家应该都差不多会了，我们接下来讲讲迭代方式走二叉树

三、二叉树的遍历（迭代）（偏难）

1.利用队列进行迭代 (易)

❗️❗️❗️❗️❗️❗️
建议不会队列的同学看看这一篇：【数据结构】栈和队列，看完这一篇就够了（万字配动图配习题）
队列的代码：有需要的自取

#define  _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include
#include
#include
struct BinaryTreeNode;
// 链式结构：表示队列 
typedef struct BinaryTreeNode* QDataType;
typedef struct QListNode
{
	struct QListNode* _next;
	QDataType _data;
}QNode;//队列中结点的结构

// 队列的结构 
typedef struct Queue
{
	QNode* _front;
	QNode* _rear;
}Queue;

// 初始化队列 
void QueueInit(Queue* q);
// 队尾入队列 
void QueuePush(Queue* q, QDataType data);
// 队头出队列 
void QueuePop(Queue* q);
// 获取队列头部元素 
QDataType QueueFront(Queue* q);
// 获取队列队尾元素 
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数 
int QueueSize(Queue* q);
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q);
// 销毁队列 
void QueueDestroy(Queue* q);

void QueueInit(Queue* q)
{
	assert(q);
	q->_front = NULL;
	q->_rear = NULL;
}
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	QNode* tmp = (QNode*)malloc(sizeof(QNode));
	tmp->_next = NULL;
	tmp->_data = data;

	if (q->_rear == NULL)
	{
		q->_front = q->_rear = tmp;
	}
	else
	{
		q->_rear->_next = tmp;
		q->_rear = tmp;
	}
}
void QueuePop(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	QNode* first = q->_front->_next;
	if (first == NULL)
		q->_rear = NULL;//处理这一步
	free(q->_front);
	q->_front = first;
}
QDataType QueueFront(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));

	return q->_front->_data;
}
QDataType QueueBack(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));

	return q->_rear->_data;
}
int QueueSize(Queue* q)
{
	assert(q);
	int n = 0;
	QNode* cur = q->_front;
	while (cur)
	{
		n++;
		cur = cur->_next;
	}
	return n;
}
int QueueEmpty(Queue* q)
{
	assert(q);
	return q->_front == NULL;
}
void QueueDestroy(Queue* q)
{
	assert(q);
	while (!QueueEmpty(q))
	{
		QNode* tmp = q->_front->_next;
		free(q->_front);
		q->_front = tmp;
	}
	q->_front = q->_rear = NULL;
}

我们走层序遍历需要怎么做呢？其实很简单，我们先入头结点入队列，然后每次在出队头元素之前把他的左孩子和右孩子带入节点，遍历队列直到队列为空。❗️❗️❗️❗️

//层序遍历
void LevelOrder(BTNode* root)
{
	//我们借用之前写过的队列
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* first = QueueFront(&q);
		//访问元素
		if (first)
			printf("%c ", first->val);
		else
			printf("NULL ");
		//入下一个元素
		if (first)
		{
			QueuePush(&q, first->left);
			QueuePush(&q, first->right);
		}
		QueuePop(&q);
	}
}

---

2.非递归实现前中后序（难）

❗️❗️❗️❗️❗️❗️❗️❗️❗️❗️❗️❗️❗️❗️❗️❗️
其实这三道题是非常类似的，我们先给大家讲最简单的前序遍历！！

2.1前序遍历

leetcode. 二叉树的前序遍历

前提提示：
一.这里的NULL我们不用访问，访问在这里相当于入一个数组（vector），不懂的同学先把他当成数组！
二. 以及这里所说的最左列为当前节点一直递归它的左子树，即上图的1 , 2，4

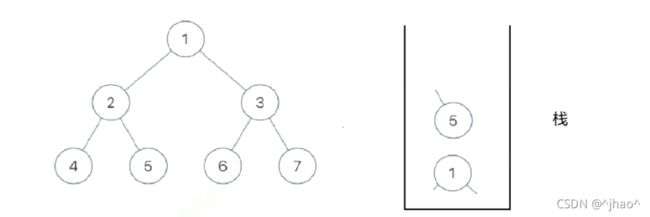
分析：我们想要利用栈对我们的二叉树进行前序遍历，我们可以观察前序遍历的时候会先遍历
1–>2–>4，我们一边遍历一边将遍历的值放入栈中看看。发现这棵树的话只剩下4，2，1的右子树就可以走完了！！！！

如何遍历右子树呢？ 实际上我们观察**（3）这颗子树我们可以发现什么，我们没有办法通过一次操作遍历完右子树，但是我们可以把3这颗子树进行拆分，我们入它的最左列节点访问再进行入栈**，就相当于遍历了（3）的左子树与每个节点的根（细品），这个时候我们遍历（7）是不是就是一次操作就能解决了？其实还可以再分一次，分到像（5）的时候，当节点的右子树为空树的时候，我们就访问他！！！

---

重要：
一棵树一定能分到没有右子树的时候，这时访问当前节点相当于访问上一个根节点的右子树
一棵树一定能分到没有右子树的时候，这时访问当前节点相当于访问上一个根节点的右子树
一棵树一定能分到没有右子树的时候，这时访问当前节点相当于访问上一个根节点的右子树
就像访问5的时候是不是相当于访问了2的右子树？是的！

---

上面没看懂，没关系，带大家再走一下每一个步骤

这里再拆分一下每一个步骤

刚开始

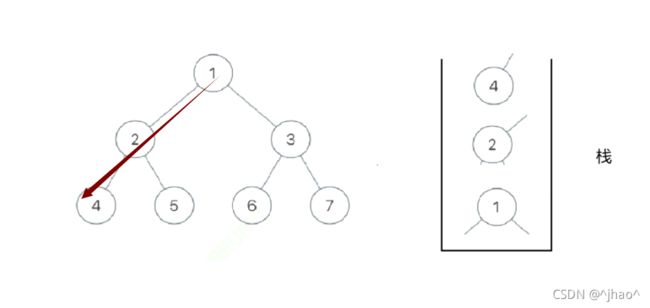
第一步：我们就访问每一个节点并且入栈（将1,2，4入栈并且放入数组），这时候我们要拿出栈顶的4，将它的右子树的最左列入栈（NULL不入栈），我们重复此操作，到2的时候，我们将它的右子树（5）及其最左列入栈并且访问，并且把2出栈，这时候的栈只有（5,1）

重复上述操作，取栈顶数据，将栈顶数据的右子树的最左列入栈之后将原栈顶数据出栈，这里5右子树为NULL不用入栈，我们栈里就只剩下1，接着入1的右子树的最左列，即3,6入栈

重复上述操作，取栈顶数据，将栈顶数据的右子树的最左列入栈之后将原栈顶数据出栈，6无右子树，就弹出了，到3的时候把3的右子树最左列带入（7），最后栈里面还有一个7
重复上述操作，取栈顶数据，将栈顶数据的右子树的最左列入栈之后将原栈顶数据出栈，把7出掉，结束！！！！

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        //利用栈进行迭代遍历
        //思路：每次遍历当前节点（cur）的左子树，再进行入栈，最后从栈中依次取出以相同的方式遍历右子树
        //可以先入最左的树
        TreeNode* cur =root;
        vector<int> retArr;//用来返回的答案
        stack<TreeNode*> s;//利用栈进行迭代遍历
        while(cur)
        {
            retArr.push_back(cur->val);
            s.push(cur);
            cur = cur->left;
        }
        //现在只要遍历栈当中的所有的右子树就遍历完所有树
        //当然遍历每个右子树也不是一次就能搞定的，我们分解成遍历每个右子树和他的左子树，...在遍历他的右子树，就类似我们的递归遍历
        while(!s.empty())
        {
            //我们可以对于栈当中的右子树一个一个处理
            cur = s.top();
            s.pop();
            cur = cur->right;
            //将右子树的最左列也都入栈
            while(cur)
            {
                //每个右子树又会带出更多的右子树....
                retArr.push_back(cur->val);
                s.push(cur);
                cur =cur->left;
            }
        }
        return retArr;
    }
};

//分析子过程，这里是第一步，将root即右子树的最左列入栈
 while(cur)
{
     //每个右子树又会带出更多的右子树....
     retArr.push_back(cur->val);
     s.push(cur);
     cur =cur->left;
 }

总结，我们面对这种题都可以先入该节点及它的最左列节点，然后我们上面这一段代码再去带出右子树当中的最左列，当我们带出来的时候相当于所有的根与左子树已经遍历完了，我们只用对右子树处理。右子树又可以被继续拆分！！！

 while(!s.empty())
        {
            //我们可以对于栈当中的右子树一个一个处理
            cur = s.top();
            s.pop();
//取出当前节点所有的右子树，没有就在后面的循环中拿出这个值（相当于访问上一个根的右子树）
            cur = cur->right;
            //将右子树的最左列也都入栈
            while(cur)
            {
                //每个右子树又会带出更多的右子树....
                retArr.push_back(cur->val);
                s.push(cur);
                cur =cur->left;
            }
        }

---

2.2中序遍历

leetcode.中序遍历

中序遍历的逻辑类似，就是我们访问顺序左子树，根，右子树。

还是用这个例子来：访问栈顶的元素之后带出该元素的右子树的最左列，再删除原来的栈顶元素
我们一开始就可以访问4（左子树相当于访问了NULL），我们走到4访问再入右子树的最左列（这里没有），再将4出栈，然后我们2的左子树访问完了，我们就直接将2入到数组，将2的右子树带进去（即带2的最左一列），再将2出栈。如下图

这时候对5进行重复操作（即访问栈顶的元素之后带出该元素的右子树的最左列，再删除原来的栈顶元素），即像4的时候5的左子树也是NULL（5的左子树访问了），我们访问5，带入右子树（这里没有），出栈。这时候栈里只剩下1，我们访问1，再拿出它的右子树的最左列（3,6）

然后我们再访问6，同理上面（左子树访问过了），然后带出它的右子树（这里没有），将6出栈，带出6的右子树，(这里没有)。

这时候栈里面只剩下3，我们访问3，把他的右子树的最左列带进去，并且把3出掉，这时候栈里面就剩下一个7

最后访问7，然后入它的右子树（NULL不访问），把7出栈。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        //类似前序遍历的迭代，只不过中序遍历是左根右
        //所以我们我们入完最左列之后从里面取得时候在放入结果的vector就可以啦
        TreeNode* cur =root;
        stack<TreeNode*> s;
        vector<int> retArr;
        //先入最左列
        while(cur)
        {
            s.push(cur);
            cur=cur->left;
        }
        while(!s.empty())
        {
            //访问当前节点并且访问它的右子树
            cur = s.top();
            s.pop();
            retArr.push_back(cur->val);
            cur=cur->right;
            while(cur)
            {
                s.push(cur);
                cur=cur->left;
            }
        }
        return retArr;
    }
};

---

2.3后序遍历

leetcode.后序遍历
后序遍历会稍微难一些，我们在按照上面的逻辑去写的时候会出现一点问题，我们用画图的方式来剖析。

我们一开始还是将根以及它的最左列入栈，根据后序遍历的左右根。

观察4是可以访问的，访问完并且可以出栈，那么1.它的条件就是当前节点的右子树为空。

现在对于2来说，我们访问它的右子树，并且不能把2出掉，因为要访问完右子树才可以出，所以我们现在将2的右子树的最左列入栈

这个时候栈顶元素5的右子树为NULL，所以我们访问5，到了现在栈顶元素就是2了，我们人为肯定知道它的右子树已经遍历了，但是程序要识别就必须要有条件，我们只有一个条件就是当前节点的右子树为空才访问栈顶元素。

结论：第二个条件应该是什么呢，我们访问当前栈顶元素（2）的时候，我们可以设置一个前驱指针，指向我们上一个访问的节点，那么我们2的上一个访问的节点是谁呢？（5）！！！，我们就可以让 cur->right == prev 即当前节点的右子树是不是指向前驱指针，若是，则该cur（2）的右子树5已经访问完了。这样就能辨别当前栈顶元素的右节点是否有访问过。

那么这个是不是巧合呢，其实不是的，想一想，我们遍历（5）这颗子树的也是遵循后序遍历的原则，最后遍历的就是子树的根（5），所以前驱指针是指向右子树的根的。

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> retArr;
        if(root ==NULL)
        return vector<int>();
        stack<TreeNode*> s;
        TreeNode* cur =root;
        TreeNode* prev =root;
        while(cur)
        {
            s.push(cur);
            cur =cur->left;
        }
        //接下来遍历每棵树的右子树
        while(!s.empty())
        {
            cur =s.top();
            if(cur->right ==NULL || cur->right == prev)
            {
                retArr.push_back(cur->val);
                prev =cur;
                //表示当前节点的右子树访问完了，就更新prev然后pop掉
                s.pop();
            }   
            else
            {
                cur = cur->right;
                while(cur)
                {
                    s.push(cur);
                    cur =cur->left;
                }
            }
        }
        return retArr;

    }
};

总结

二叉树的初阶就在这里告一段落啦，大家觉得有帮助可以给博主一键三连，这对我真的很重要，谢谢啦。