【分布式技术专题】「分布式技术架构」一文带你厘清分布式事务协议及分布式一致性协议的算法原理和核心流程机制(Paxos篇)
概念简介
Paxos是一种基于消息传递具有高度容错特性的一致性算法,是目前公认的解决分布式一致性问题最有效的算法之一。
发展历史
Paxos算法的发展历史追溯到古希腊,当时有一个名为“Paxos“的小岛, 岛上采用一会的形式通过法令, 议会中议员通过信使进行消息传递,议员与信使都是兼职的,他们随时都有可能会离开议会,并且信使有可能传递重复的信息,也有可能一去不复返,因此议会要保证在这种情况下法令仍然能够正确的产生,并且不会起冲突。
Paxos算法分析
对于Paxos算法而言要解决上述信息传递的一致性问题,那么要保证一下几点:
- 在这些提案中,只有一个被选定
- 如果没有提案被提出,就不会有选定的提案
- 当提案被选定以后,进程应该可以获取被选定的提案信息
对于一致性来说,安全性需求如下
- 只有被提出的提案才能被选定
- 只有一个提案被选定
- 如果某个进程认为某个提案被选定了,那么这个提案必须是真的被选定的那个
三种参与角色
- Proposer(提议者)
- Acceptor(决策者)
- Leamner(最终决策学习者)
问题场景分析
一个元素参与者可能扮演多个角色 (Proposer | Acceptor | Leamner) ,假设不同的参与者之间可以通过收发消息来进行通信。每个参与者以任意的速度执行,可能会因为出错而停止,也可能会重启,消息在传输过程中可能会出现不可预知的延迟,也有可能会重复或者丢失,但消息不会被损坏,即消息内容不能被篡改。
Paxos算法场景问题分析
首先,我们采用将建立角色处理模式的场景化分析,先从Acceptor的模式开始处理和分析,分析对应的执行流程以及对应的问题。
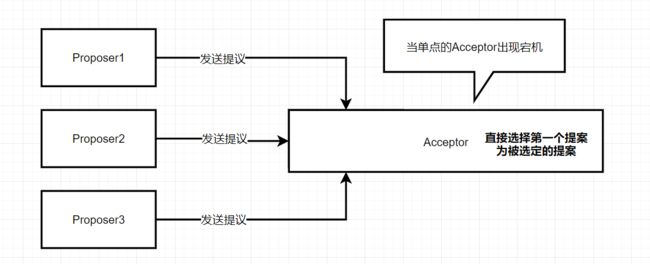
单个Acceptor模式
在处于单Acceptor模式下的时候,如以下图所示。
最简单的选定方式是只有一个Acceptor, Proposer发送给该Acceptor提案以后, Acceptor直接选择第一个提案为被选定的提案。但这种做法一旦Acceptor出问题, 整个系统将无法正常工作。
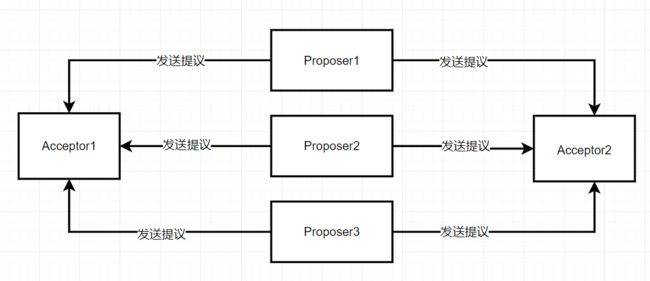
多个Acceptor模式
Proposer向多个Acceptor集合发送提案, 每个Acceptor都可能会批准(Accept) 该提案, 当足够多个Acceptor批准这个提案的时候, 我们就认为该提案被选定了。
实现一致性的条件约束(1)
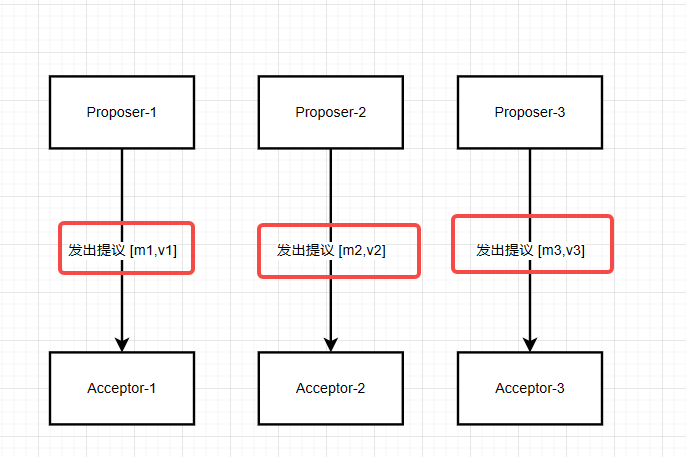
在没有失败和消息丢失的情况下,如果我们希望即使只有一个提案被提出,仍然可以选出一个提案,1个Acceptor必须批准他收到的第一个提案。
该条件约束所出现的问题
如果多个提案被不同的Proposer同时提出, 这可能会导致虽然每个Acceptor都批准了他收到的第一个提案, 但是没有一个提案是多个人批准的,也就是没有多数的Acceptor集合,如下图所示。
为了解决此问题所以引入了【实现一致性的条件约束(2)】进行数据控制。
实现一致性的条件约束(2)
一个提案被选定需要被半数以上的Acceptor接受。
它是在【实现一致性的条件约束(1)】的基础上, 一个Acceptor能够批准不止一个提案。我们使用全局的编号来唯一的标识每一个Acceptor批准的提案, 当一个具有某Value的提案被半数以上的Acceptor批准以后, 我们就认为该Value被选定。
注意:提案和value不是一个概念, 提案是由一个编号与value组成的结构体, 因此我们用【编号,Value】来表示一个提案。
提案的结构体分析
提案的信息数据结构体主要有:提案编号+value两部分组成。
- 提案编号:给每个提案加上一个提案编号,表示提案被提出的顺序,不同的编号可以有相同的内容。
- value:提案的内容
该条件约束所出现的问题
虽然允许多个提案被选定, 但必须保证所有被选定的提案都具有相同的value值,否则又会出现不一致。
为了解决此问题所以引入了【实现一致性的条件约束(3)】进行数据控制。
实现一致性的条件约束(3)
如果提案编号为M, Value为V的提案(即【M,V】)被选定了,那么所有比M_编号更高的, 且被选定的提案, 其Value值必须也是V。
因为提案编号是全序的, 【实现一致性的条件约束(3)】就保证了只有一个Value值被选定这一关键安全性属性。同时,一个提案被选定,其首先必须被至少一个Acceptor批准, 因此我们可以通过满足如下条件来满足【实现一致性的条件约束(3)】。
案例推荐
假设总的有5个Acceptor,Proposer2提出 [M1,V1] 的提案,Acceptor2~5(半数以上)均接受了该提案,于是对于Acceptor 2~5和Proposer2来讲, 它们都认为V1被选定。
Acceptor1刚刚从宕机状态恢复过来(之前Acceptor1没有收到过任何提案) , 此时Proposer1向Acceptor1发送了[M2, V2] 的提案(V2且M2>M1) ,对于Acceptorl来讲, 这是它收到的第一个提案。根据【实现一致性的条件约束(1)】(一个Acceptor必须接受它收到的第一个提案) ,从而Acceptor1必须接受该提案!同时Acceptor1认为V2被选定,这就出现了两个问题。
问题分析
-
Acceptor1认为V2被选定,Acceptor2~5和Proposer2认为V1被选定,出现了不一致。
-
V1被选定了,但是编号更高的被Acceptor1接受的提案[M2,V2] 的value为V2,且V2不等于V1。且V2的编号还高于V1。
实现一致性的条件约束(4)
如果一个提案【M,V】被选定后, 那么之后任何Proposer产生的编号更高的提案, 其Value的值都为V。
问题分析
如何确保在某个Value为V的提案被选定后, Proposer 提出的编号更高的提案的Value都是V呢?
实现分析
任意的N和V, 如果提案 [ N,V ] 被提出,那么存在一个半数以上的Acceptor组成的集合S,需要执行以下两个操作步骤:
- 集合S内的每个Acceptor都没有批准过编号小于N的提案。
- 如果Acceptor已经接受过提案,那么就向Proposer响应已经接受过的编号小于N的最大编号的提案。
Proposer生成提案
对于一个Proposer来说, 获取那些已经通过的提案远比预测未来可能会通过的提案来的简单。因此Proposer在产生一个编号为M的提案时, 必须要知道当前某一个将要或已经被半数以上Acceptor批准的编号小于M但未最大的编号的提案。并且,Proposer会要求所有Acceptor都不要批准任何编号小于M的提案。
Proposer生成提案之前(Prepare阶段)
应该先去学习已经被选定或者可能被选定的value,然后以该value作为自己提出的提案的value。如果没有value被选定, Proposer才可以自己决定value的值。这样才能达成一致。这个学习的阶段是通过一个 【Prepare阶段】 请求实现的。
- 向Proposer承诺保证不再接受任何编号小于N的提案
- 如果Acceptor已经接受过提案,那么就向Proposer响应已经接受过的编号小于N的最大编号的提案
提案生成算法
如果Proposer收到了平数以上的Acceptor的响应, 那么它就可以生成编号为N, Value为V的提案[N,V] 。这里的V是所有的响应中编号最大的提案的Value。如果所有的响应中都没有提案, 那么此时V就可以由Proposer自己选择。
Proposer生成提案之后(Accept请求)
Proposer将该提案发送给半数以上的Acceptor集合, 并期望这些Acceptor能接受该提案。我们称该请求为Accept请求。
注意:此时接受Accept请求的Acceptor集合不一定是之前响应Prepare请求的Acceptor集合
Acceptor批准提案
-
Acceptor可以忽略任何请求(包括Prepare请求和Accept请求) 而不用担心破坏算法的安全性。因此, 我们这里要讨论的是什么时候Acceptor可以响应一个请求。
-
一个Acceptor只要尚未响应过任何编号大于N的Prepare请求, 那么他就可以接受这个编号为N的提案。
算法总结
阶段一
- Proposer选择一个提案编号M, 然后向Acceptor的某个超过半数的子集成员发送编号为M的Prepare请求。
- 如果一个Acceptor收到一个编号为M的Prepare请求, 且编号M大于该Acceptor已经响应的所有Prepare请求的编号, 那么它就会把已经批准过的最大的编号的提案作为相应反馈给Proposer, 同时该Acceptor会承诺不会在批准任何编号小于M的提案。
阶段二
- 如果Proposer收到来自半数以上的Acceptor对于其发出的编号为M的Prepare请求的响应,那么它就会发送一个针对【M,V】提案的Accept请求给Acceptor。
注意:V的值就是收到的响应中编号最大的提案的值,如果响应中不包含任何提案,那么他就是任意值
- 如果Acceptor收到的这个针对【M, V】的提案的Accept请求, 只要该Acceptor尚未对编号大于M的Prepare请求作出响应, 他就可以通过这个提案。
看到这里是不是觉得和我们分布式事务中的2PC的思路和流程差不多啊!
通知学习Learner的方案
方案1
一旦Acceptor批准了一个提案, 就将该提案发送给所有的Leamer
方案2
让所有的Acceptor将它们对提案的批准情况, 统一发送给一个Learner, 再由它通知其他的Learner
方案3
方案2的主节点存在单点问题, 可以将主Leaner的范围扩大, 即Acceptor可以将批准信息发送给一个特定的Learner集合, 该集合中每个Leamer都可以在一个提案被选定后通知其他Leaner。
给你们的问题
-
设置多少个Acceptor最为合适?
-
如何控制每个Acceptor最多只能批准一个提案?