单调栈图文详解（附Java模板）

                                                                             啥是"单调栈"，它能解决什么样的问题？          

---

仰望天空，妳我亦是行人.✨
个人主页——微风撞见云的博客
数据结构与算法专栏的文章图文并茂生动形象简单易学！欢迎大家来踩踩~
希望本文能够给读者带来一定的帮助文章粗浅，敬请批评指正！

---

---

单调栈的概念

单调栈分为单调递增栈和单调递减栈，通过使用单调栈我们可以访问到最近一个比它大（小）的元素。

     单调递增栈：单调递增栈就是从栈底到栈顶数据是依次递增，通常是寻找某方向第一个比它小的元素。
     单调递减栈：单调递减栈就是从栈底到栈顶数据是依次递减，通常是寻找某方向第一个比它大的元素。

适用场景

什么情况适合用单调栈来解决实际问题呢？

     通常是在数组中需要通过比较前后元素的大小关系来找最近的比它大（小）的元素问题时，可以使用单调栈进行求解。

情形示例

        1. 寻找左边第一个小于它的数

                  题目描述： 给定一个长度为 n ≤ 10 ^5 的数组 a，输出每个数左边第一个比它小的数，如果不存在则输出 − 1。

        【常规思路】

                  双重循环来做，第一重循环枚举每个数，第二重循环找出指定区间类第一个满足条件的数。然而这种做法的复杂度是O（n^2）利用单调栈，我们可以将复杂度降低至O(n)。

    在指针 i 从左往右遍历的过程中，我们可以用一个栈来保存 i 左边的所有元素（不包括i指向的元素），下标越大的元素越接近栈顶，下标越小的元素越接近栈底。

    每次我们访问栈顶，只要栈顶元素大于等于 a [ i ]，我们就将栈顶元素弹出，直至栈顶元素小于 a [ i ] ，此时输出栈顶元素并将 a [ i ] 压入栈中。 由于栈中保存了 i 左边的所有元素，所以只要有答案，则答案一定在栈中。

     由于每个元素一定会被压入一次且至多弹出一次，因此操作次数至多是2n，故总时间复杂度为O(n)。

---

            让我们来看看过程图解

        初始化 原数组 和 结果数组，我们去寻找最右边的数字5，左边最近的、小于它的数值。

        准备将第一个元素“2” 入栈，由于栈空，咱们直接修改结果数组第一个元素值为-1（默认填充了-1，所以我们这里就不修改了）。然后将元素入栈。

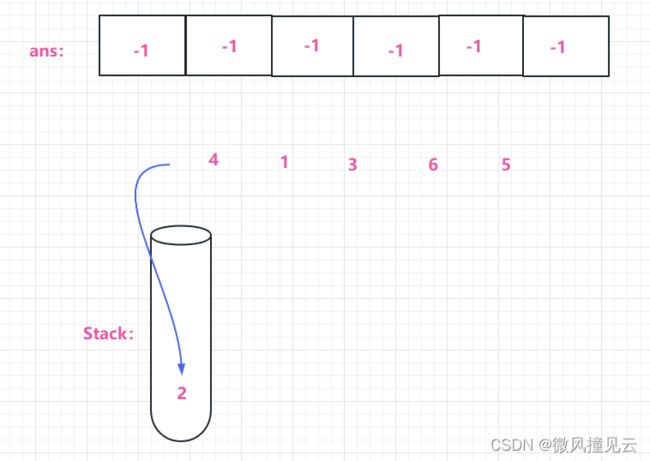
        准备将第二个元素“4” 入栈，此时栈非空，但是栈顶元素小于当前元素，所以，记录结果数组对应值为 栈顶元素的值，然后入栈当前元素。

        准备将第三个元素“1” 入栈，此时栈非空，并且栈顶元素大于当前元素，所以我们应该依次弹栈，直到栈顶元素小于当前元素或者栈空；记录结果数组对应值为栈顶元素的值（这里已经栈空了，所以填充-1），然后入栈当前元素。

        准备将第四个元素“3” 入栈，此时栈非空，并且栈顶元素小于当前元素，所以记录结果数组对应值为 栈顶元素的值，然后入栈当前元素。

        准备将第五个元素“6” 入栈，此时栈非空，并且栈顶元素小于当前元素，所以记录结果数组对应值为 栈顶元素的值，然后入栈当前元素。

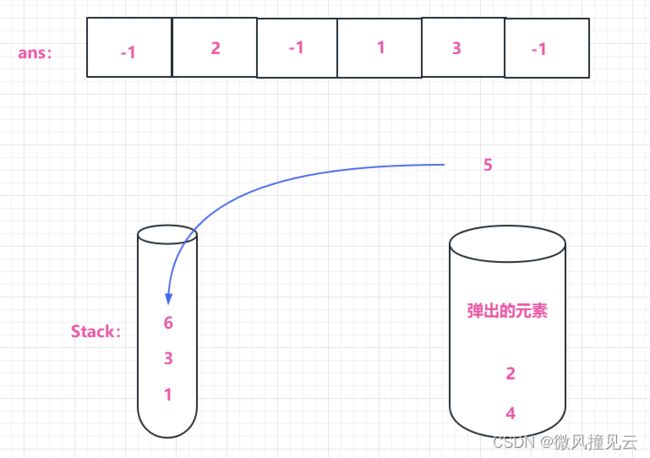
        准备将最后一个元素“5” 入栈，此时栈非空，并且栈顶元素大于当前元素，所以我们应该依次弹栈，直到栈顶元素小于当前元素或者栈空；记录结果数组对应值为栈顶元素的值（这里只弹出一个元素就满足了，并且栈非空，所以填充栈顶元素即可），然后入栈当前元素；此时得到的结果数组即为最终结果.

        Java代码如下：

public class Main {
    static int N = (int) (1e5 + 10);
    static int[] a = new int[N], ans = new int[N];
    static Deque<Integer> stack = new LinkedList<>();
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static void main(String[] args) throws IOException {
        in.nextToken();
        int n = (int) in.nval;
        for (int i = 0; i < n; i++) {//存数组
            in.nextToken();
            a[i] = (int) in.nval;
        }

        for (int i = 0; i < n; i++) {//单调栈模板（注意是数值）
            while (!stack.isEmpty() && stack.peekFirst() >= a[i]) stack.poll();
            if (!stack.isEmpty()) ans[i] = stack.peekFirst();
            else ans[i] = -1;
            stack.push(a[i]);
        }

        for (int i = 0; i < n; i++) {//输出结果
            System.out.print(ans[i] + " ");
        }
    }
}

        下面，我们再来看看其他几种情况，基本上都是大同小异。

        2. 寻找左边第一个小于它的数的下标

                  题目描述： 给定一个长度为 n ≤ 10 ^5 的数组 a，输出每个数左边第一个比它小的数的下标，如果不存在则输出 − 1。

                  我们只需要注意几个点，在当前条件下，咱们栈中存的是下标，而不是值，所以需要修改两个地方：a[stack.peekFirst()] 而不是stack.peekFirst()，不再是a[i]，而是存储对应的下标，具体要修改的地方我已经在注释里写出来了。

        Java代码如下：

public class Main {
    static int N = (int) (1e5 + 10);
    static int[] a = new int[N], ans = new int[N];
    static Deque<Integer> stack = new LinkedList<>();
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static void main(String[] args) throws IOException {
        in.nextToken();
        int n = (int) in.nval;
        for (int i = 0; i < n; i++) {//存数组
            in.nextToken();
            a[i] = (int) in.nval;
        }

        for (int i = 0; i < n; i++) {//单调栈模板（注意是下标）
            while (!stack.isEmpty() && a[stack.peekFirst()] >= a[i]) stack.poll();//注意这里的第二个条件是a[stack.peekFirst()] 而不是stack.peekFirst()
            if (!stack.isEmpty()) ans[i] = stack.peekFirst();
            else ans[i] = -1;
            stack.push(i);//这里也不再是a[i]，而是存储对应的下标
        }

        for (int i = 0; i < n; i++) {//输出结果
            System.out.print(ans[i] + " ");
        }
    }
}

        3. 寻找右边第一个大于它的数

                  题目描述： 给定一个长度为 n ≤ 10 ^5 的数组 a，输出每个数右边第一个比它大的数，如果不存在则输出 − 1。

                  之前我们是在一个数的左边去寻找，所以让栈去保存这个数左边的所有数，类似地，现在需要让栈去保存这个数右边的所有数。
考虑将数组翻转（倒序遍历），因此情形三变成了「寻找一个数左边第一个大于它的数」，属于情形一

        Java代码如下：

public class Main {
    static int N = (int) (1e5 + 10);
    static int[] a = new int[N], ans = new int[N];
    static Deque<Integer> stack = new LinkedList<>();
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static void main(String[] args) throws IOException {
        in.nextToken();
        int n = (int) in.nval;
        for (int i = 1; i <= n; i++) {//存数组
            in.nextToken();
            a[i] = (int) in.nval;
        }

        for (int i = n - 1; i > 0; i--) {//单调栈模板（注意是数值）
            while (!stack.isEmpty() && stack.peekFirst() <= a[i]) stack.poll();
            if (!stack.isEmpty()) ans[i] = stack.peekFirst();
            stack.push(a[i]);
        }

        for (int i = 0; i < n; i++) {//输出结果
            System.out.print(ans[i] + " ");
        }
    }
}

        4. 寻找右边第一个大于它的数的下标

                  题目描述： 给定一个长度为 n ≤ 10 ^5 的数组 a，输出每个数右边第一个比它大的数的下标，如果不存在则输出 − 1。

                  结合情形二和情形三即可写出代码。

        Java代码如下：

public class Main {
    static int N = (int) (1e5 + 10);
    static int[] a = new int[N], ans = new int[N];
    static Deque<Integer> stack = new LinkedList<>();
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static void main(String[] args) throws IOException {
        in.nextToken();
        int n = (int) in.nval;
        for (int i = 0; i < n; i++) {//存数组
            in.nextToken();
            a[i] = (int) in.nval;
        }

        for (int i = n-1; i > 0; i--) {//单调栈模板（注意是下标）
            while (!stack.isEmpty() && a[stack.peekFirst()] <= a[i]) stack.poll();
            if (!stack.isEmpty()) ans[i] = stack.peekFirst();
            stack.push(i);
        }

        for (int i = 0; i < n; i++) {//输出结果
            System.out.print(ans[i] + " ");
        }
    }
}

总结以上情形：
    遍历顺序（以怎样的顺序遍历数组 a ）；
    比较方式（如何比较当前元素和栈顶元素）；
    栈中存储的是什么（是元素本身还是元素的下标）。

模板例题 —— 洛谷 P5788 【模板】单调栈

洛谷 P5788 【模板】单调栈

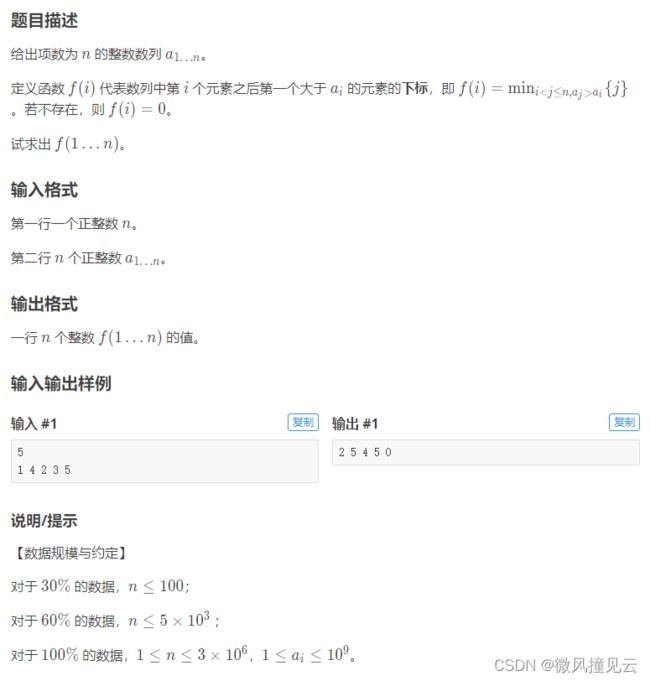
Java代码如下：（不知道为啥，Java的没AC，C++这样写是AC的）

public class Main {
    static int N = (int) (3e6 + 10);
    static int[] a = new int[N], ans = new int[N];
    static Deque<Integer> stack = new LinkedList<>();
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static void main(String[] args) throws IOException {
        in.nextToken();
        int n = (int) in.nval;
        for (int i = 1; i <= n; i++) {//存数组
            in.nextToken();
            a[i] = (int) in.nval;
        }

        for (int i = n; i > 0; i--) {//单调栈模板（注意是下标）
            while (!stack.isEmpty() && a[stack.peekFirst()] <= a[i]) stack.poll();
            if (!stack.isEmpty()) ans[i] = stack.peekFirst();
            stack.push(i);
        }

        for (int i = 1; i <= n; i++) {//输出结果
            System.out.print(ans[i] + " ");
        }
    }
}

进阶例题 —— LeetCode 42. 接雨水

42. 接雨水

    思路：
        遍历heights数组，将其中的元素加入单调递减栈，如果当前柱子的高度大于栈顶柱子的高度，不断出栈，相当于找到左边比当前柱子矮的位置，然后每次出栈之后都要累加一下面积。

    复杂度：
        时间复杂度O(n)，n是heights的长度，数组中的每个元素最多入栈出栈一次。
        空间复杂度O(n)，栈的空间，最多不会超过heights的长度

    Java代码如下：（相比之前的代码有些许变化，因为这道题需要做的事情会稍微多一点，注释我打在了代码中，请大家耐心阅读）

import java.util.Deque;
import java.util.LinkedList;

public class Main {
    public static void main(String[] args) {
        int[] height = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
        System.out.println(trap(height));
    }
    
    public static int trap(int[] height) {
//        int[] height = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
        int ans = 0;//总雨水量
        Deque<Integer> stack = new LinkedList<>();
        int n = height.length;
        for (int i = 0; i < n; ++i) {
        //这里是在干这样一件事情：把当前的这根柱子作为“右柱”，把栈顶的元素作为“中间柱”也叫“接水柱”
        //（此时还没弹栈），然后把“接水柱”前面的那个柱子，作为“左柱”，有了“左柱”和“右柱”，
        //咱们的“接水柱”就能接水了，但是它只能接到左右两边更低的那个柱子高度的水。
            while (!stack.isEmpty() && height[stack.peek()] <= height[i]) {
//上面这个式子说明：“右柱”比栈顶也就是“接水柱”更高，这样的话才能准备接水。
//否则的话，就是满足单调递减栈的，那么我们继续入栈。
                int top = stack.pop();//拿出前一个柱子
                if (stack.isEmpty()) break;//如果拿出这根柱子后，前面没有元素了，那就接不了雨水了，因为接雨水的话，至少需要左右两边都有柱子才行。
                int left = stack.peek();//记录一下拿到的这根柱子的左边那根柱子的高度
                int currWidth = i - left - 1;//看图推算。
//上面这个式子有人会说：不都是1吗？其实不是的，加入我们连续加入两个0高度的柱子（有点奇怪），
//这个时候，不符合单调栈的定义，那么我们会弹出一个栈，但是由于高度为0，我们也不会因此得到更多的面积，
//因为s = h * w； 不过，这个时候你会发现，中间空出来了一个，准确的说是两格，
//因为前面还有一个0高度的柱子，那么我们下次找到“右柱”的时候就会发现：这个宽度并非是1，
//而是隔开了一定的距离，这个距离和下标有关，看图稍加推导得出距离为：i - left - 1；
                int currHeight = Math.min(height[left], height[i]) - height[top];//用左右两边更小的柱子来接雨水（木桶原理）
                ans += currWidth * currHeight;//记录本次所接的雨水量
            }
            stack.push(i);//经过上面一顿操作之后，咱们的栈又满足单调性了，于是将当前元素的下标入栈。
        }
        return ans;
    }

}

我知道，看到这里的你一定特别不容易！！！祝你收获满满，更上一层楼~

---

结语

    初学一门技术时，总有些许的疑惑，别怕，它们是我们学习路上的点点繁星，帮助我们不断成长。

    文章粗浅，希望对大家有帮助！

    参考文章：单调栈详解、单调栈